Как выполнить одновыборочный t-тест в sas

Одновыборочный t-критерий используется для определения того, соответствует ли среднее значение совокупности определенному значению.

В этом руководстве объясняется, как выполнить одновыборочный t-тест в SAS.

Пример: образец t-теста в SAS

Предположим, ботаник хочет знать, равна ли средняя высота определенного вида растений 15 дюймам. Она берет случайную выборку из 12 растений и записывает высоту каждого из них в дюймах.

Высоты: 14, 14, 16, 13, 12, 17, 15, 14, 15, 13, 15, 14.

Используйте следующие шаги, чтобы выполнить t-тест для одного образца, чтобы определить, действительно ли средняя высота этого вида растений составляет 15 дюймов.

Шаг 1: Создайте данные.

Сначала мы будем использовать следующий код для создания набора данных в SAS:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*print dataset*/
proc print data =my_data; 

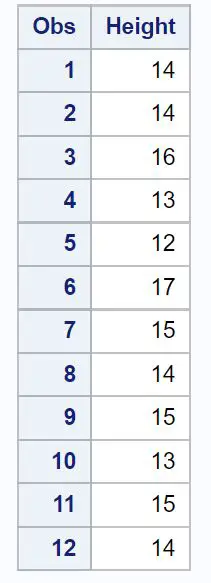
Шаг 2. Выполните t-критерий для одной выборки.

Далее мы воспользуемся proc ttest для выполнения t-теста на примере:

 /*perform one sample t-test*/
proc ttest data =my_data sides = 2 alpha = 0.05 h0 = 15 ;
    varHeight ;
run ;

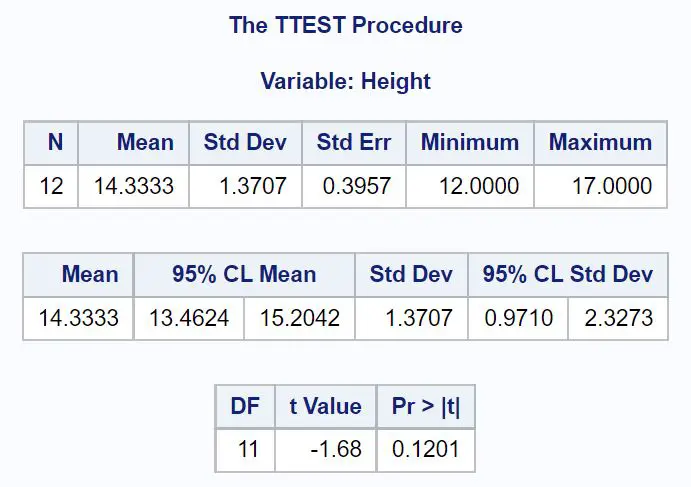
В первой таблице представлена описательная статистика для нашей выборки, в том числе:

• N (всего наблюдений): 12
• Среднее (выборочное среднее): 14,3333
• Std Dev (выборочное стандартное отклонение): 1,3707.
• Стандартная ошибка (стандартная ошибка, рассчитываемая как s/ √n ): 0,3957
• Минимум (минимальное значение): 12
• Максимум (максимальное значение) 17

Во второй таблице показан 95% доверительный интервал для истинного среднего значения генеральной совокупности:

• 95% ДИ для μ: [13,4624, 15,2042]

В третьей таблице отображается статистика t-теста и соответствующее значение p:

• статистика t-теста: -1,68
• р-значение: 0,1201

Примечание . Статистика теста рассчитывалась следующим образом:

• t статистика теста = ( x – µ) / (s/ √n )
• статистика t-теста = (14,3333-15) / (1,3707/√ 12 )
• статистика t-теста = -1,68

Напомним, что одновыборочный t-критерий использует следующие нулевые и альтернативные гипотезы:

• H ₀ : μ = 15 дюймов
• H _A : мкм ≠ 15 дюймов

Поскольку значение p ( .1201 ) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.

Это означает, что у нас недостаточно доказательств, чтобы сказать, что средняя высота некоторых видов растений отличается от 15 дюймов.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные статистические тесты в SAS:

Как выполнить знаковый ранговый тест Уилкоксона в SAS
Как выполнить односторонний дисперсионный анализ в SAS