3 типа логистической регрессии (включая примеры)

Логистическая регрессия относится к любой модели регрессии, в которой переменная ответа является категориальной.

Существует три типа моделей логистической регрессии:

• Бинарная логистическая регрессия : переменная ответа может принадлежать только к одной из двух категорий.
• Полиномиальная логистическая регрессия : переменная ответа может относиться к одной из трех или более категорий, и между категориями нет естественного порядка.
• Порядковая логистическая регрессия : переменная ответа может относиться к одной из трех или более категорий, и между категориями существует естественный порядок.

В следующей таблице суммированы эти различия:

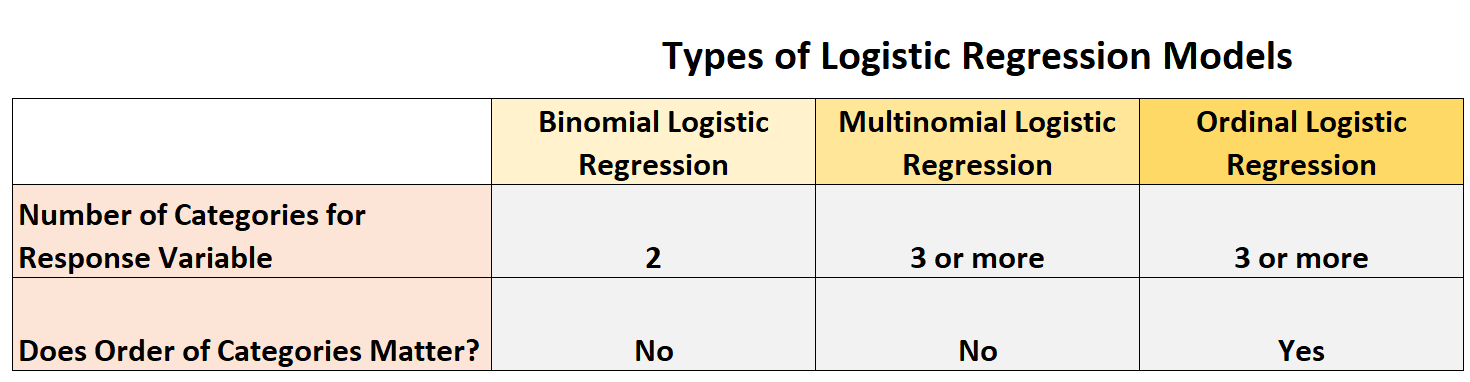
В этом руководстве представлено краткое объяснение каждого типа модели логистической регрессии, а также приведены примеры каждой из них.

Тип №1: бинарная логистическая регрессия.

Модели бинарной логистической регрессии — это тип логистической регрессии, в которой переменная ответа может относиться только к двум категориям.

Вот некоторые примеры:

Пример 1: Драфт НБА

Предположим, специалист по спортивным данным хочет использовать переменные-предсказатели (1) очков, (2) подборов и (3) передач, чтобы предсказать вероятность того, что данный баскетболист колледжа будет выбран в НБА.

Поскольку для переменной ответа существует только два возможных результата (письменный или неписаный), специалист по обработке данных будет использовать модель биномиальной логистической регрессии.

Пример 2: Обнаружение спама

Предположим, компания хочет использовать переменные-предсказатели (1) количество слов и (2) страну происхождения, чтобы предсказать вероятность того, что данное электронное письмо является спамом.

Поскольку для переменной ответа существует только два возможных результата (спам или неспам), компания будет использовать модель биномиальной логистической регрессии.

Тип № 2: Полиномиальная логистическая регрессия.

Модели полиномиальной логистической регрессии — это тип логистической регрессии, в которой переменная ответа может попасть в одну из трех или более категорий, и между категориями нет естественного порядка.

Вот некоторые примеры:

Пример 1: Политические предпочтения

Предположим, политолог хочет использовать переменные-предикторы (1) годовой доход и (2) годы образования, чтобы предсказать вероятность того, что человек проголосует за одного из четырех разных кандидатов в президенты.

Поскольку для переменной ответа существует более двух возможных результатов (есть четыре потенциальных кандидата) и между результатами нет естественного порядка, политолог будет использовать модель полиномиальной логистической регрессии.

Пример 2: Спортивные предпочтения

Предположим, спортивный аналитик хочет использовать переменные-предсказатели (1) часы просмотра телевизора в неделю и (2) возраст, чтобы предсказать вероятность того, что человек выберет баскетбол, футбол или бейсбол в качестве своего любимого вида спорта.

Поскольку для переменной ответа существует более двух возможных результатов (есть три вида спорта), спортивный аналитик будет использовать модель полиномиальной логистической регрессии.

Тип №3: Порядковая логистическая регрессия

Модели порядковой логистической регрессии — это тип логистической регрессии, в которой переменная ответа может относиться к одной из трех или более категорий, и между категориями существует естественный порядок.

Вот некоторые примеры:

Пример 1: школьные оценки

Предположим, консультант колледжа хочет использовать переменные-предсказатели (1) средний балл, (2) балл ACT и (3) балл SAT, чтобы предсказать вероятность того, что человек поступит в колледж, который можно отнести к категории «плохой», «посредственный». . », «хорошо» или «отлично».

Поскольку существует более двух возможных результатов (существует четыре классификации качества школы) для переменной ответа и существует естественный порядок между результатами, школьный консультант будет использовать модель порядковой логистической регрессии.

Пример 2: Рейтинги фильмов

Предположим, кинокритик хочет использовать переменные-предсказатели (1) общую продолжительность показа и (2) жанр, чтобы предсказать вероятность того, что данный фильм получит рейтинг от 1 до 10.

Поскольку существует более двух возможных результатов (возможных оценок 10) для переменной ответа и существует естественный порядок между результатами, кинокритик будет использовать модель порядковой логистической регрессии.

Дополнительные ресурсы

В следующих руководствах представлена более подробная информация о моделях логистической регрессии:

Введение в логистическую регрессию
6 гипотез логистической регрессии
4 примера использования логистической регрессии в реальной жизни