Введение в треугольное распределение
Треугольное распределение представляет собой непрерывное распределение вероятностей с функцией плотности вероятности в форме треугольника.
Он определяется тремя значениями:
- Минимальное значение имеет
- Максимальное значение b
- Максимальное значение c
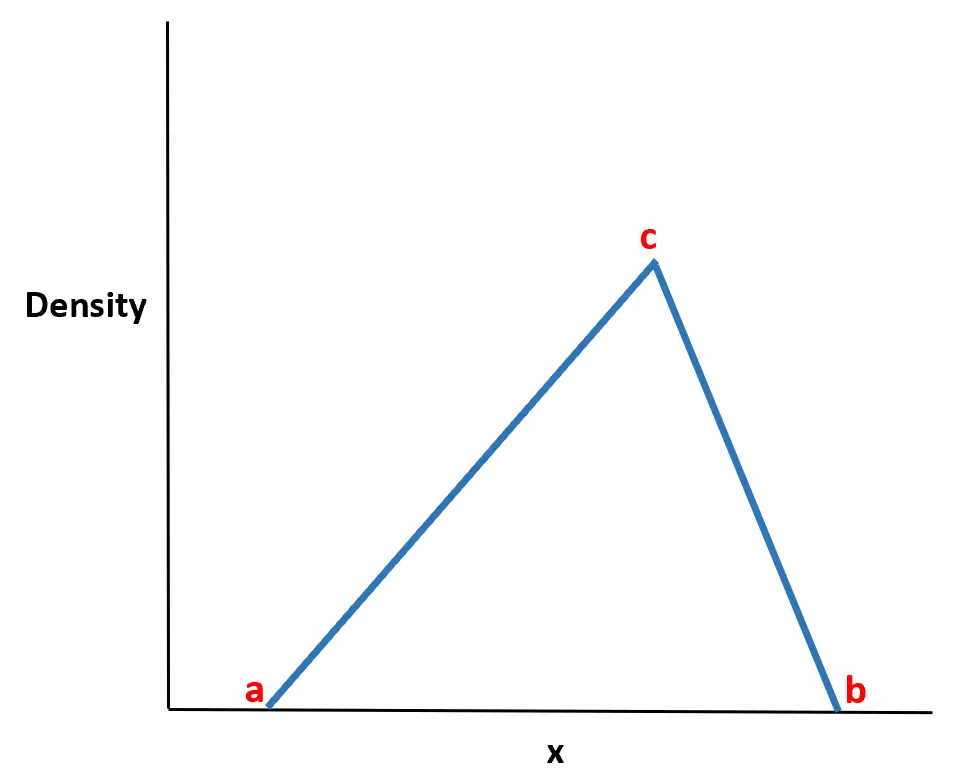
Название распределения происходит от того, что функция плотности вероятности имеет форму треугольника.
Оказывается, это распределение чрезвычайно полезно в реальном мире, поскольку мы часто можем оценить минимальное значение (a), максимальное значение (b) и наиболее вероятное значение (c), которое примет случайная величина . часто может моделировать поведение случайных величин, используя треугольное распределение, зная только эти три значения.
Например, ресторан может оценить, что его общий объем продаж на предстоящую неделю составит минимум 10 000 долларов, максимум 30 000 долларов и, скорее всего, 25 000 долларов.

Используя только эти три числа, они могли бы использовать треугольное распределение, чтобы определить вероятность совершения определенного количества продаж.
Свойства треугольного распределения
Треугольное распределение обладает следующими свойствами:
PDF:
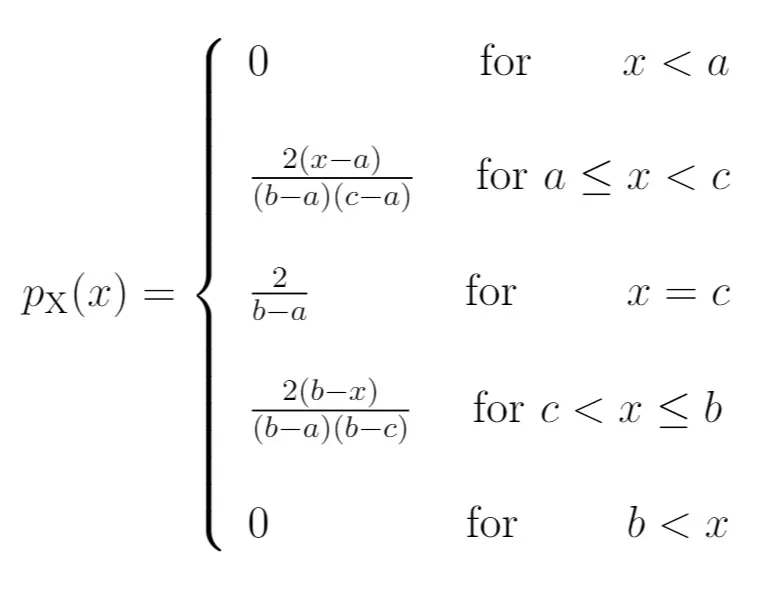
ВПР:
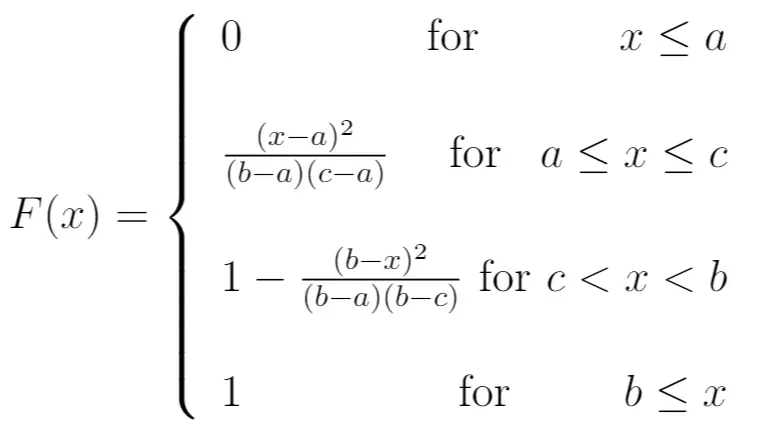
Среднее: (а + б + в) / 3
Режим: с
Дисперсия: (a 2 + b 2 + c 2 – ab – ac – bc) / 18
Пример использования треугольного распределения
Вернемся к предыдущему примеру. Допустим, ресторан оценивает, что его общий объем продаж на предстоящей неделе составит минимум 10 000 долларов, максимум 30 000 долларов и, скорее всего, 25 000 долларов.

Какова вероятность того, что общий объем продаж ресторана составит менее 20 000 долларов?
Чтобы ответить на этот вопрос, мы можем задать x = общий объем продаж. Мы знаем, что x находится между минимальным значением a , равным 10 000 долларов, и максимальным значением c , равным 25 000 долларов.
Итак, согласно PDF-файлу, мы можем использовать следующее уравнение, чтобы найти вероятность того, что общий объем продаж ресторана составит менее 20 000 долларов:
- P(X < 20 000 долларов США) = (xa) 2 / ((ba)(ca))
- P(X < 20 000 долларов США) = (20 000–10 000) 2 / ((30 000–10 000)(25 000–10 000))
- P(X <20 000 долларов США) = 0,333
Вероятность того, что общий объем продаж ресторана составит менее 20 000 долларов, равна 0,333 .
Каков средний ожидаемый объем продаж ресторана?
Мы можем рассчитать ожидаемый средний объем продаж, используя формулу для среднего значения, приведенную ранее:
- Среднее = (a + b + c)/3
- Среднее = (10 000 долларов США + 30 000 долларов США + 25 000 долларов США) / 3
- Среднее = 21 667 долларов США
Средний ожидаемый объем продаж составляет 21 667 .
Дополнительные ресурсы
В следующих руководствах представлены сведения о других часто используемых дистрибутивах:
Нормальное распределение
Биномиальное распределение
Распределение рыбы
Геометрическое распределение