Как выполнить апостериорный тест тьюки-крамера в excel

Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.

Допущения , используемые в ANOVA, следующие:

Нулевая гипотеза (H ₀ ): µ ₁ = µ ₂ = µ ₃ = … = µ _k (средние значения равны для каждой группы)

Альтернативная гипотеза: (Ха): хотя бы одно из средств отличается от других.

Если значение p ANOVA ниже уровня значимости, мы можем отвергнуть нулевую гипотезу и заключить, что у нас есть достаточно доказательств, чтобы сказать, что по крайней мере одно из групповых средних значений отличается от других.

Однако это не говорит нам о том, какие группы отличаются друг от друга. Это просто говорит нам о том, что не все средние значения по группам одинаковы. Чтобы точно узнать, какие группы отличаются друг от друга, нам нужно провести апостериорный тест.

Наиболее часто используемым апостериорным тестом является тест Тьюки-Крамера , который сравнивает среднее значение между каждой парной комбинацией групп.

В следующем примере показано, как выполнить тест Тьюки-Крамера в Excel.

Пример: тест Тьюки-Крамера в Excel

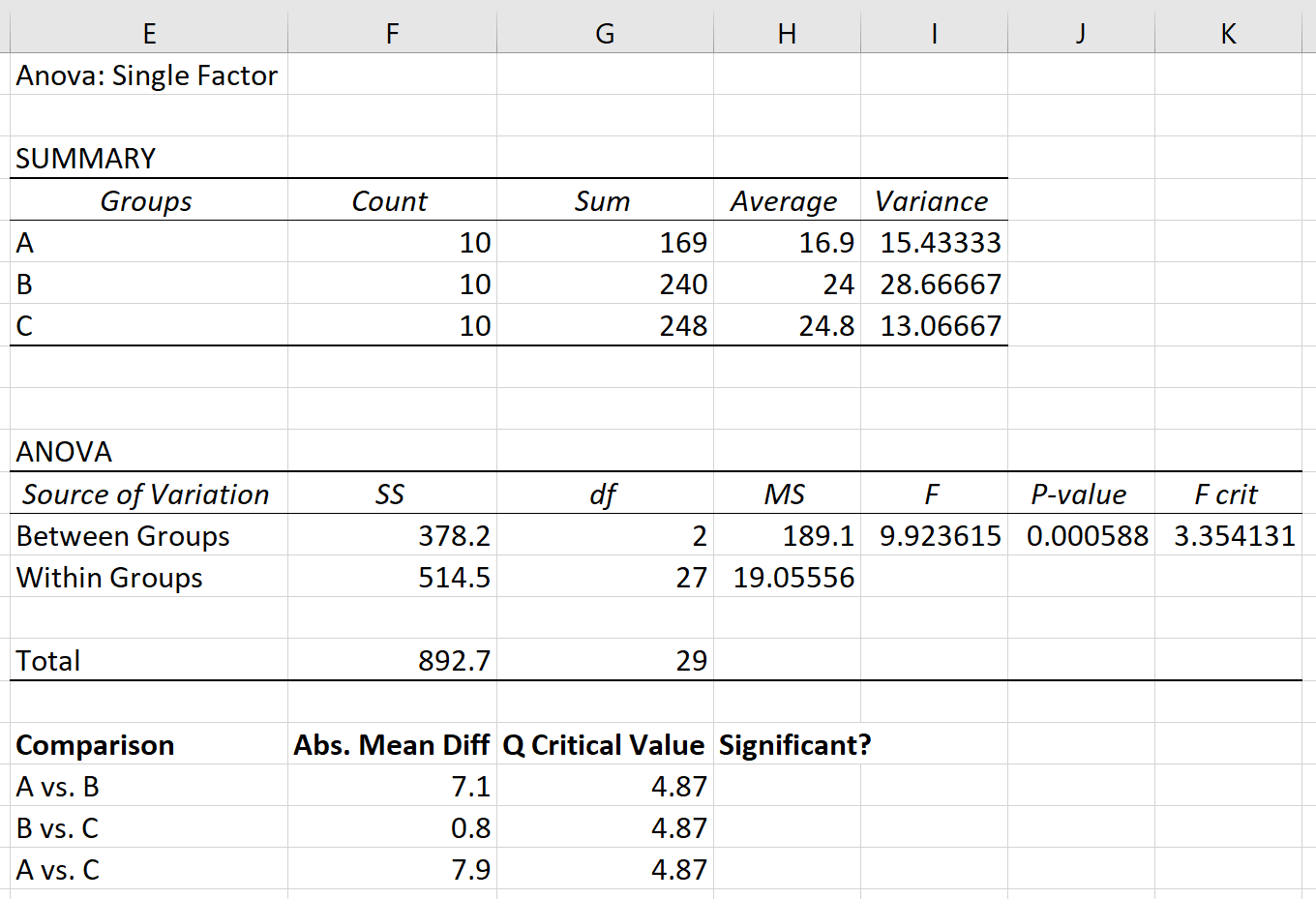
Предположим, мы выполняем однофакторный дисперсионный анализ для трех групп: A, B и C. Результаты одностороннего дисперсионного анализа показаны ниже:

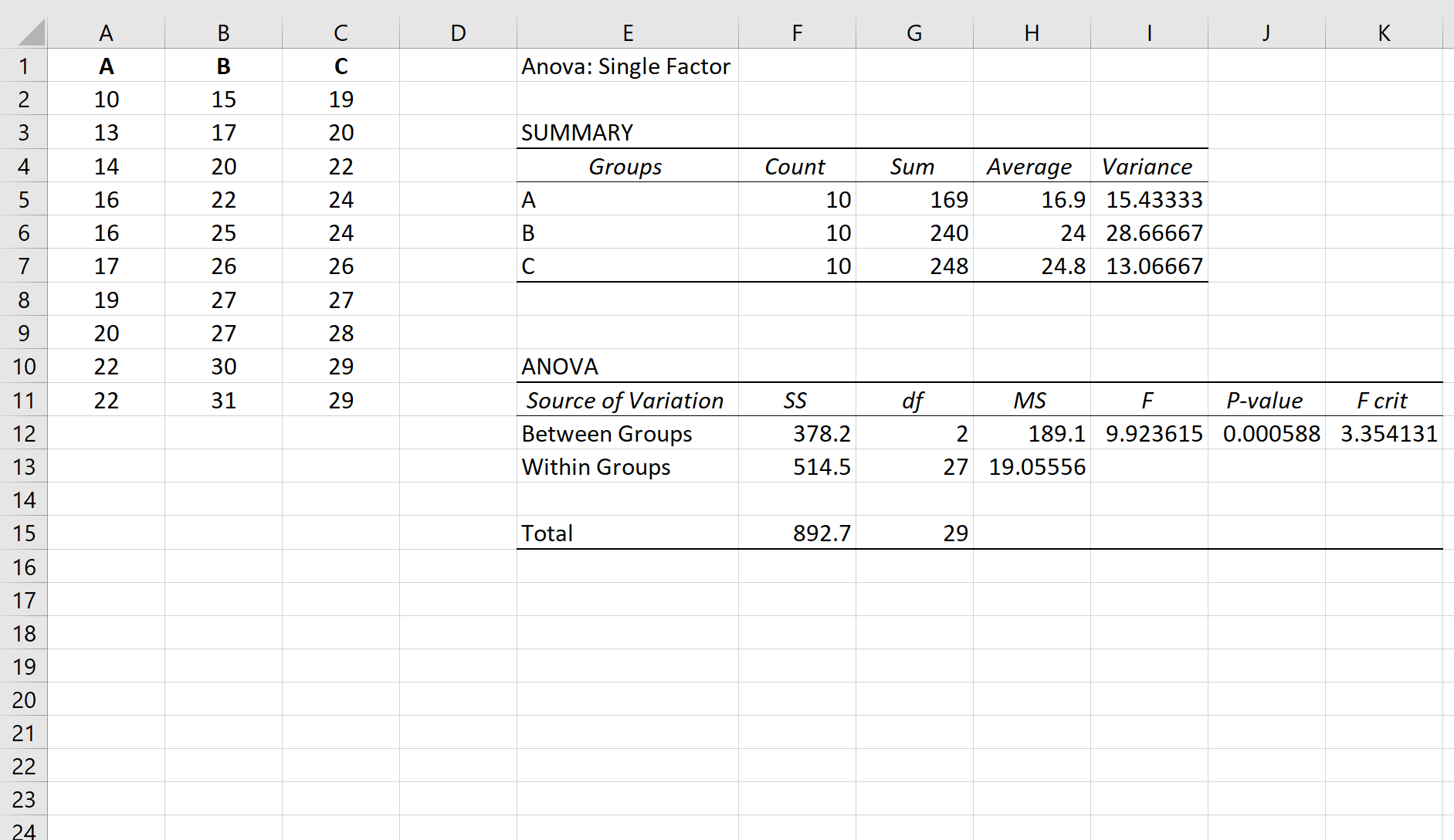
Связанный: Как выполнить однофакторный дисперсионный анализ в Excel

P-значение таблицы ANOVA составляет 0,000588 . Поскольку это значение p меньше 0,05, мы можем отвергнуть нулевую гипотезу и сделать вывод, что средние значения между тремя группами не равны.

Чтобы точно определить , какие групповые средние значения различаются, мы можем выполнить апостериорный тест Тьюки-Крамера, выполнив следующие шаги:

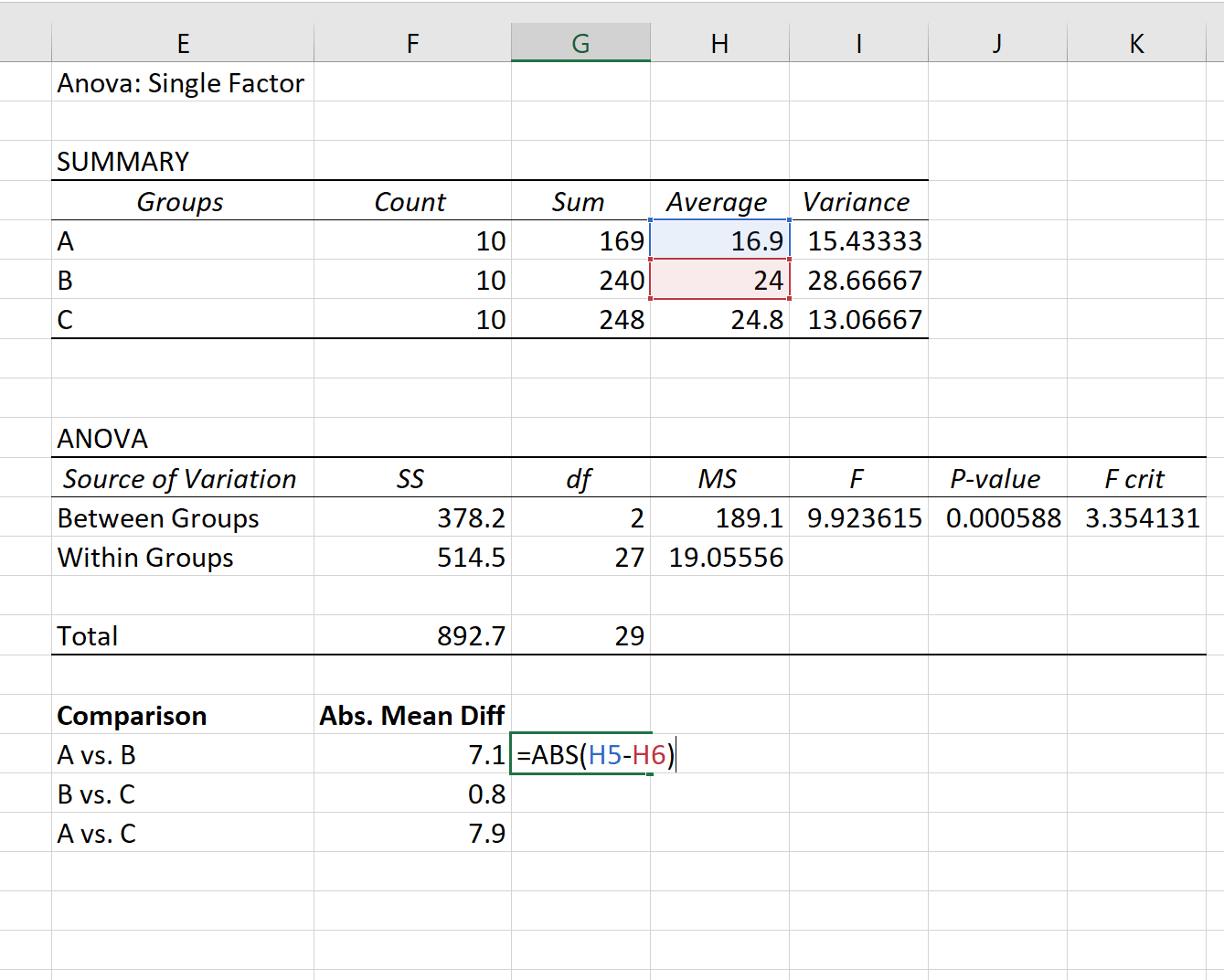
Шаг 1: Найдите абсолютную среднюю разницу между каждой группой.

Сначала мы найдем абсолютную среднюю разницу между каждой группой, используя средние значения, перечисленные в первой таблице результатов ANOVA:

Шаг 2: Найдите критическое значение Q.

Далее нам нужно найти критическое значение Q по следующей формуле:

Критическое значение Q = Q*√(s ² _{сгруппировано} / n.)

Золото:

• Q = значение диапазона таблицы студентов Q
• s ² _{объединено} = дисперсия объединена по всем группам
• нет. = Размер выборки для данной группы

Чтобы найти значение Q, вы можете обратиться к таблице Q стьюдентизированного диапазона, которая выглядит следующим образом:

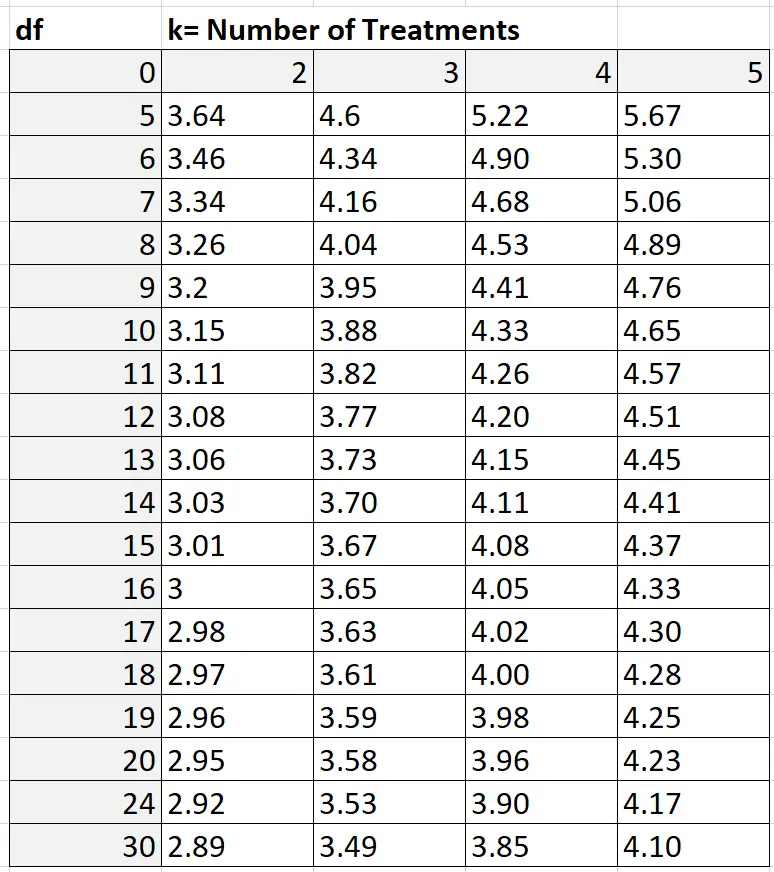
В нашем примере k = количество групп, т.е. k = 3. Степени свободы рассчитываются как: nk = 30 – 3 = 27. Поскольку 27 не показано в таблице выше, мы можем использовать консервативную оценку 24. Исходя из k = 3 и df = 24, мы находим, что Q = 3,53 .

Объединенную дисперсию можно рассчитать как среднее дисперсий групп, которое оказывается равным 19,056 .

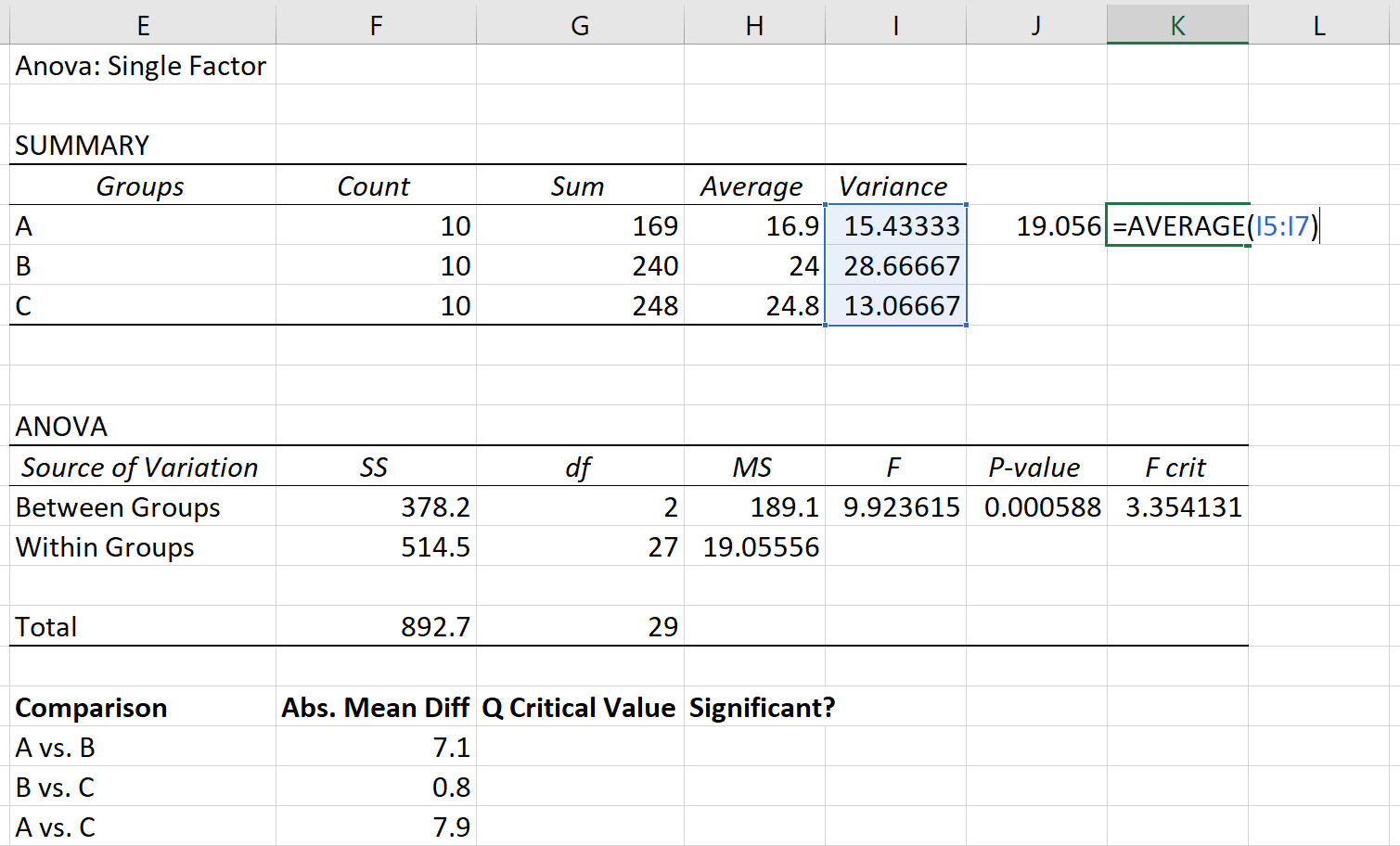
Наконец, размер выборки каждой группы составляет 10 человек.

Таким образом, наше критическое значение Q можно рассчитать следующим образом:

Критическое значение Q = Q*√(s ² _{сгруппировано} /n.) = 3,53*√(19,056/10) = 4,87 .

Шаг 3: Определите, какие групповые средства отличаются .

Наконец, мы можем сравнить абсолютную среднюю разницу между каждой группой с критическим значением Q. Если абсолютная средняя разница больше критического значения Q, то разница между групповыми средними статистически значима:

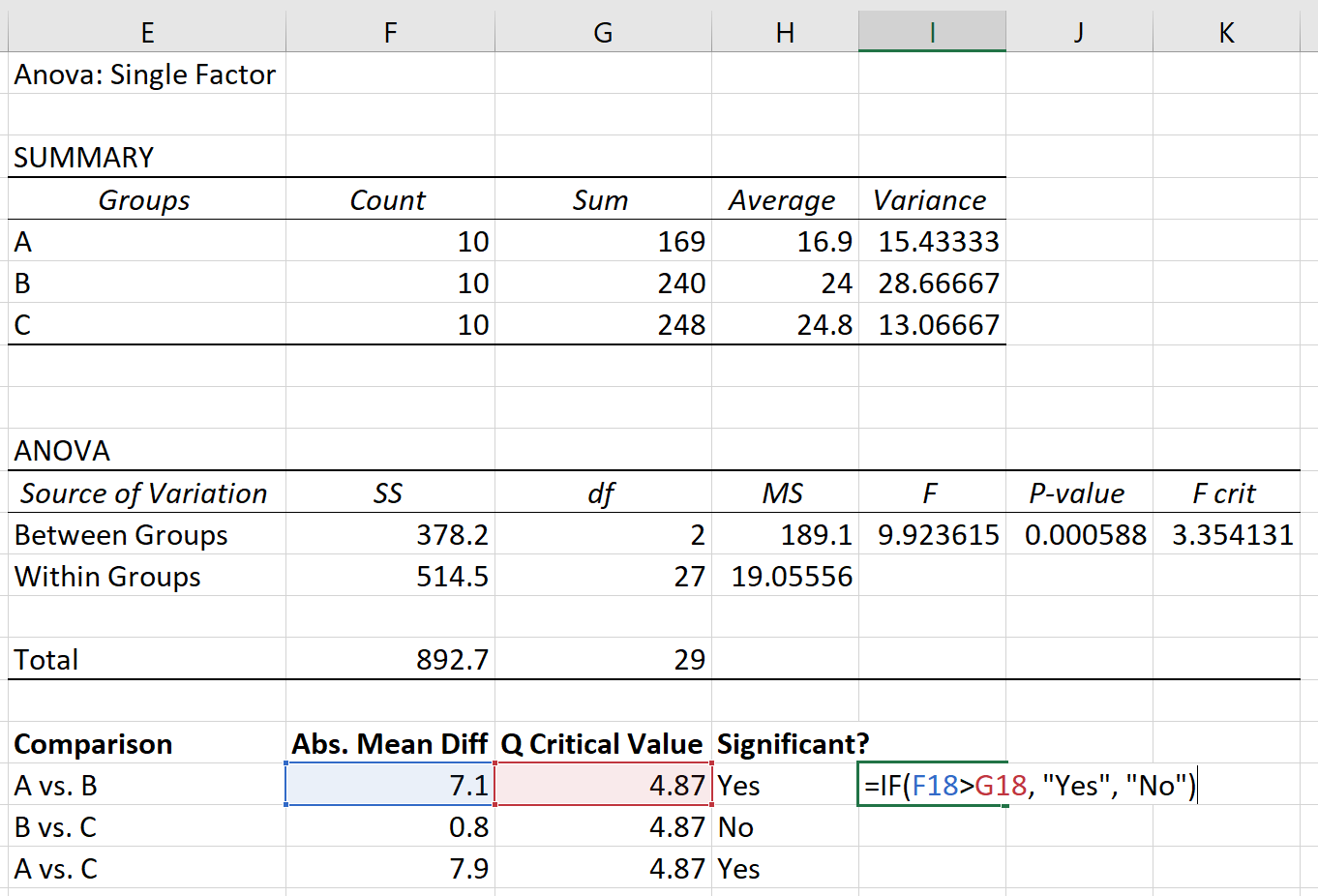
На основании апостериорного теста Тьюки-Крамера мы обнаружили следующее:

• Разница в средних значениях между группой А и группой Б статистически значима.
• Разница в средних значениях между группой B и группой C не является статистически значимой.
• Разница в средних значениях между группой А и группой С статистически значима.

Дополнительные ресурсы

Как выполнить однофакторный дисперсионный анализ в Excel
Руководство по использованию апостериорного тестирования с помощью ANOVA