Тьюки против. бонферрони против. шеффе: какой тест следует использовать?
Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.
Если общее значение p таблицы ANOVA ниже определенного уровня значимости, то у нас есть достаточно доказательств, чтобы сказать, что по крайней мере одно из групповых средних значений отличается от других.
Однако это не говорит нам о том, какие группы отличаются друг от друга. Это просто говорит нам о том, что не все средние значения по группам одинаковы.
Чтобы точно знать, какие группы отличаются друг от друга, нам нужно провести апостериорный тест , который сможет контролировать частоту ошибок на каждое семейство .
К трем наиболее часто используемым апостериорным тестам относятся:
- Метод Тьюки
- Метод Шеффе
- Метод Бонферрони
В этом руководстве представлен обзор каждого метода, а также инструкции о том, какой апостериорный тест использовать в зависимости от ситуации.
Метод Тьюки
Апостериорный тест Тьюки следует использовать, когда вы хотите провести попарные сравнения между группами, то есть, когда размеры выборки в каждой группе равны.
Если размеры выборок не равны, вы можете использовать модифицированную версию теста, известную как тест Тьюки-Крамера.
Термин «попарно» означает, что мы хотим одновременно сравнивать только средние значения двух групп.
Например, предположим, что у нас есть три группы: A, B, C.
Апостериорный тест Тьюки позволил бы нам провести следующие парные сравнения:
- мкА = мкБ
- мкА = мкКл
- мкБ = мкК
Обратите внимание, что для k групп всего существует k ( k -1)/2 возможных парных сравнений.
Метод Шеффе
Апостериорный тест Шеффе следует использовать, когда мы хотим выявить все возможные контрасты между групповыми средними. Этот тест позволяет сравнивать более двух средних значений одновременно, в отличие от апостериорного теста Тьюки.
Например, предположим, что у нас есть четыре группы: A, B, C, D.
Апостериорный тест Шеффе позволит проводить сложные сравнения, такие как:
- мкА – мкВ = мкС – мкД
- мкА + мкД = мкБ + мкС
Хотя апостериорный тест Шеффе является наиболее гибким, он также является наиболее консервативным и дает самые широкие доверительные интервалы. Это означает, что он имеет самую низкую статистическую мощность и самую низкую способность обнаруживать истинные различия между группами.
Обратите внимание, что апостериорный критерий Шеффе можно использовать независимо от того, равны ли размеры групповой выборки.
Метод Бонферрони
Апостериорный тест Бонферрони следует использовать, если вы хотите заранее выполнить ряд запланированных сравнений.
Например, предположим, что у нас есть три группы — A, B, C — и мы заранее знаем, что нас интересуют только следующие сравнения:
- мкА = мкБ
- мкБ = мкК
Когда у нас есть определенный набор запланированных сравнений, которые мы хотели бы провести заранее, апостериорный тест Бонферрони дает самые узкие доверительные интервалы, а это означает, что он обладает наибольшей способностью обнаруживать истинные различия между группами интересов. .
Обратите внимание, что апостериорный критерий Бонферрони также можно использовать независимо от того, равны ли размеры групповой выборки.
Какой метод вам следует использовать?
Следующее дерево решений поможет вам решить, какой апостериорный тест следует использовать в зависимости от ситуации:
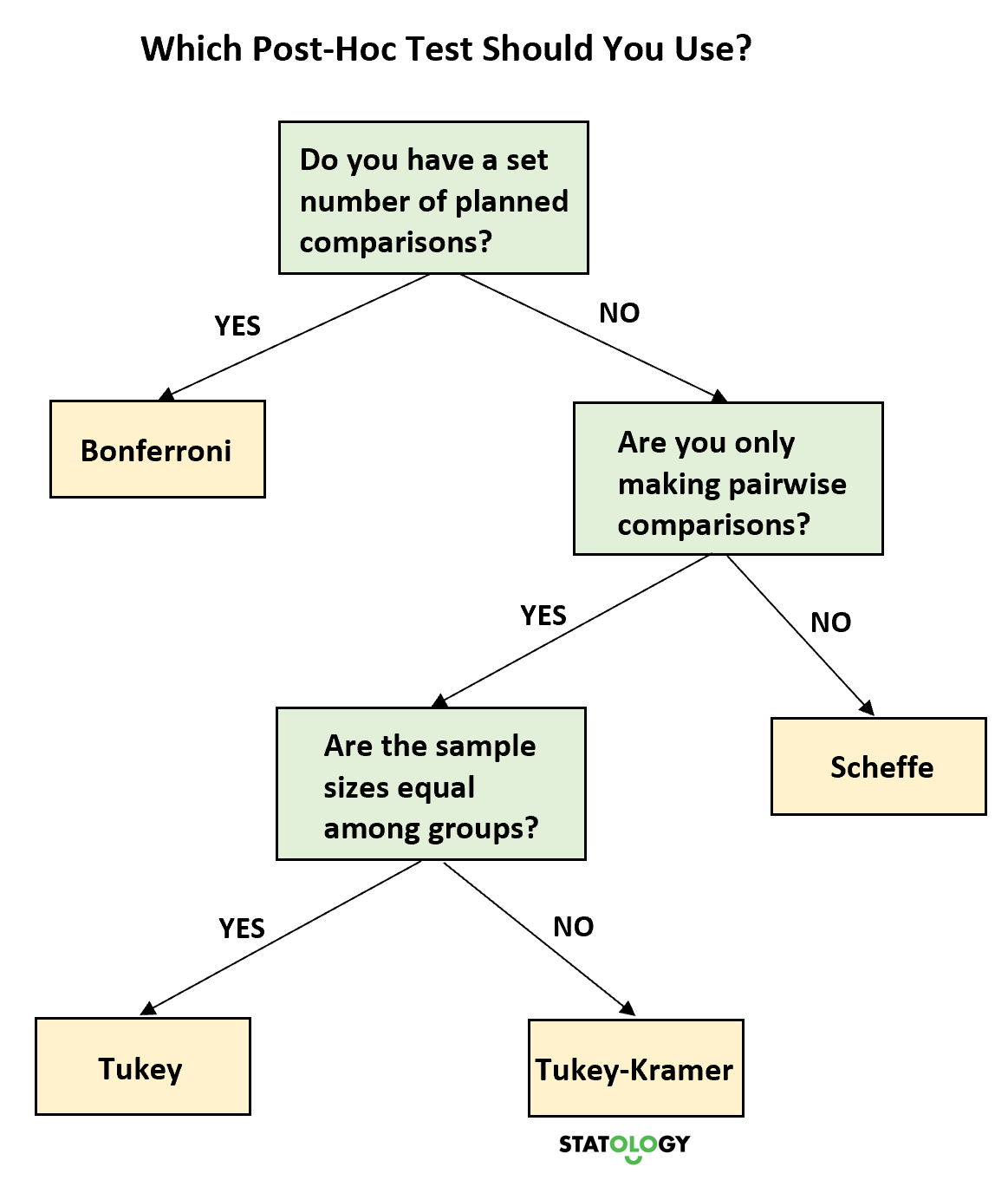
Последние мысли
Какой бы апостериорный тест вы ни выбрали, вы должны решить, прежде чем проводить эксперимент.
Это не позволяет вам выбрать апостериорный тест после эксперимента, который с большей вероятностью даст значимые результаты, что считается нечестной исследовательской практикой.
Тем не менее, большинство статистических программ способны выполнять такие апостериорные тесты, поэтому вам редко придется рассчитывать их вручную.