Как выполнить тест тьюки в r
Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.
Если общее значение p таблицы ANOVA ниже определенного уровня значимости, то у нас есть достаточно доказательств, чтобы сказать, что по крайней мере одно из групповых средних значений отличается от других.
Однако это не говорит нам о том, какие группы отличаются друг от друга. Это просто говорит нам о том, что не все средние значения по группам одинаковы. Чтобы точно узнать, какие группы отличаются друг от друга, нам нужно провести апостериорный тест .
Одним из наиболее часто используемых апостериорных тестов является тест Тьюки , который позволяет нам выполнять попарные сравнения между средними значениями каждой группы, контролируя при этом частоту семейных ошибок .
В этом руководстве объясняется, как выполнить тест Тьюки в R.
Примечание. Если какая-либо из групп вашего исследования считается контрольной, вместо этого вам следует использовать тест Даннетта в качестве апостериорного теста.
Пример: тест Тьюки в R
Шаг 1: Подберите модель ANOVA.
Следующий код показывает, как создать поддельный набор данных с тремя группами (A, B и C) и подогнать к данным однофакторную модель ANOVA, чтобы определить, равны ли средние значения каждой группы:
#make this example reproducible set.seed(0) #create data data <- data.frame(group = rep (c("A", "B", "C"), each = 30), values = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data head(data) group values 1 A 2.6900916 2 A 0.7965260 3 A 1.1163717 4 A 1.7185601 5 A 2.7246234 6 A 0.6050458 #fit one-way ANOVA model model <- aov (values~group, data=data) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) group 2 98.93 49.46 30.83 7.55e-11 *** Residuals 87 139.57 1.60 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Мы видим, что общее значение p из таблицы ANOVA составляет 7,55e-11 . Поскольку это число меньше 0,05, у нас есть достаточно оснований говорить о том, что средние значения в каждой группе не равны. Итак, мы можем провести тест Тьюки, чтобы точно определить, какие именно групповые средние значения отличаются.
Шаг 2: Выполните тест Тьюки.
Следующий код показывает, как использовать функцию TukeyHSD() для выполнения теста Тьюки:
#perform Tukey's Test TukeyHSD(model, conf.level= .95 ) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = values ~ group, data = data) $group diff lwr upr p adj BA 0.9777414 0.1979466 1.757536 0.0100545 CA 2.5454024 1.7656076 3.325197 0.0000000 CB 1.5676610 0.7878662 2.347456 0.0000199
Значение p указывает, существует ли статистически значимая разница между каждой программой. Результаты показывают, что существует статистически значимая разница между средней потерей веса каждой программы на уровне значимости 0,05.
Особенно:
- Значение P для разницы средних значений между B и A: 0,0100545.
- Значение P для разницы средних значений между C и A: 0,0000000.
- Значение P для разницы средних значений между C и B: 0,0000199.
Шаг 3: Визуализируйте результаты.
Мы также можем использовать функциюplot(TukeyHSD()) для визуализации доверительных интервалов:
#plot confidence intervals plot(TukeyHSD(model, conf.level= .95 ), las = 2 )
Примечание. Аргумент las указывает, что метки делений должны быть перпендикулярны (las=2) оси.
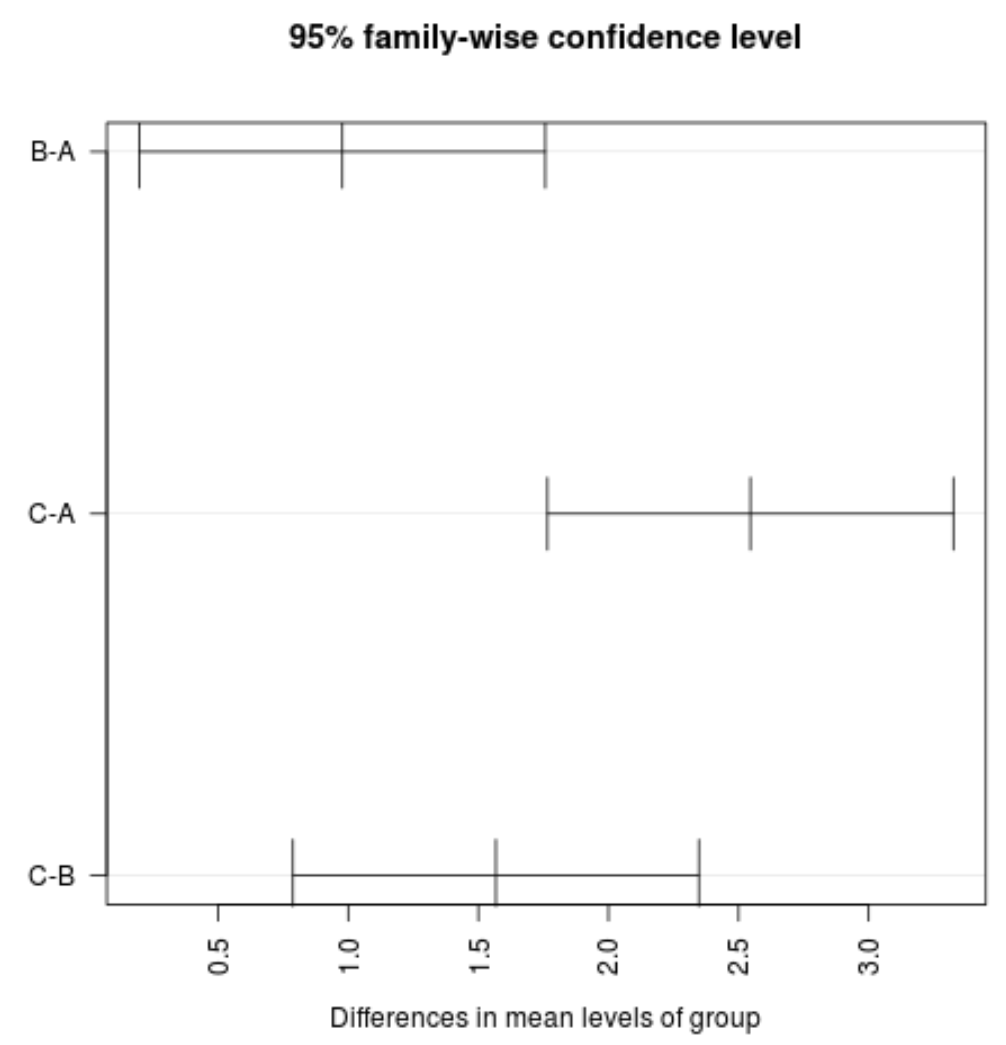
Мы видим, что ни один из доверительных интервалов для среднего значения между группами не содержит нулевого значения, что указывает на статистически значимую разницу в средних потерях между тремя группами. Это соответствует тому, что все значения p для наших тестов гипотез составляют менее 0,05.
По данному конкретному примеру можно сделать следующие выводы:
- Средние значения группы С значительно превышают средние значения групп А и В.
- Средние значения группы Б значительно выше средних значений группы А.
Дополнительные ресурсы
Руководство по использованию апостериорного тестирования с помощью ANOVA
Как выполнить односторонний дисперсионный анализ в R
Как выполнить двусторонний дисперсионный анализ в R