Как интерпретировать сиг. значения (двусторонние) в spss

Часто, когда вы выполняете статистическое тестирование в SPSS, выходная таблица содержит Sig. стоимость (двусторонняя) .

Это значение представляет собой двустороннее p-значение теста.

Если это значение ниже вашего уровня значимости (обычный выбор — 0,05 или 0,01), вы можете отклонить нулевую гипотезу вашего теста.

В этом руководстве представлены примеры интерпретации Sig. (двустороннее) значение различных статистических тестов.

Пример 1: t-критерий для одной выборки

Одновыборочный t-критерий используется для проверки того, соответствует ли среднее значение совокупности определенному значению.

Например, предположим, что ботаник хочет знать, равна ли средняя высота определенного вида растений 15 дюймам. Она берет случайную выборку из 12 растений и записывает высоту каждого из них в дюймах.

Затем он использует эту выборку для выполнения одновыборочного t-теста со следующими нулевыми и альтернативными гипотезами:

• H ₀ : μ = 15 (реальная средняя численность населения равна 15 дюймам)
• H _A : μ ≠ 15 (фактическая средняя численность населения не равна 15 дюймам)

Она запускает этот одновыборочный t-тест в SPSS и получает следующие результаты:

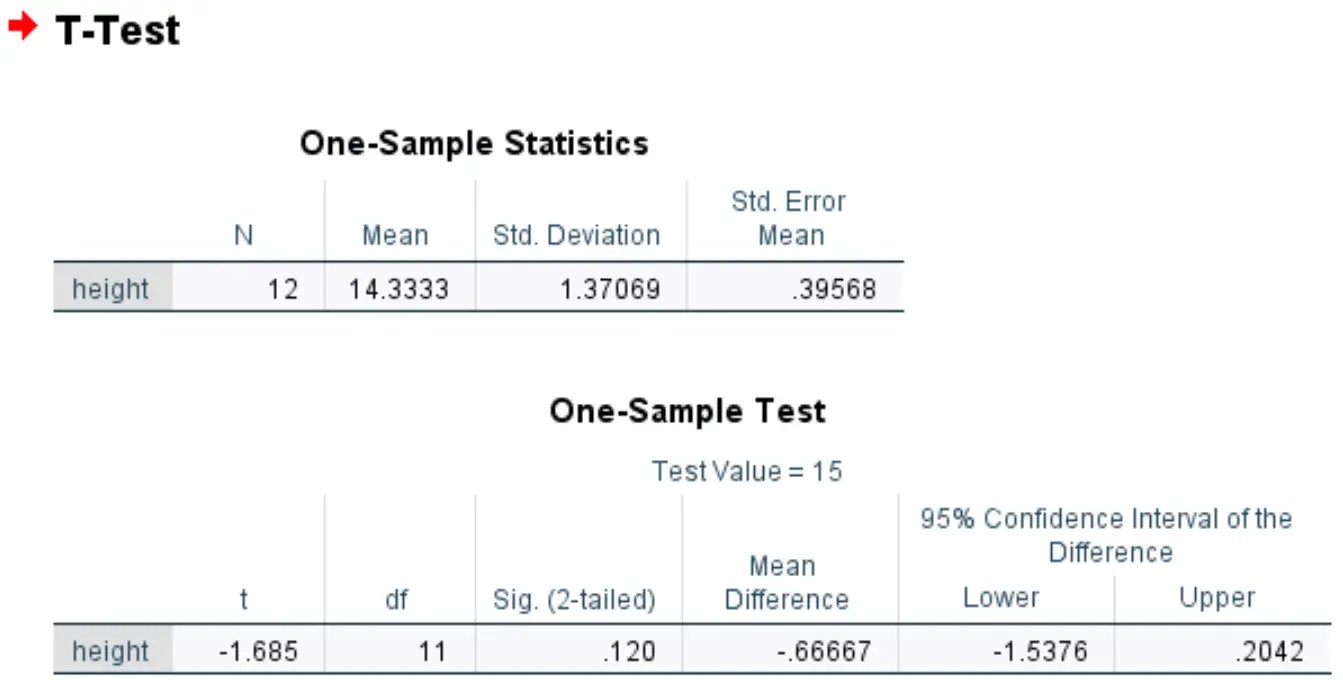
Сиг. Значение (двустороннее) — 0,120 .

Это представляет собой двустороннее значение p, которое соответствует значению -1,685 с 11 степенями свободы.

Поскольку значение p теста (0,120) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.

Другими словами, у нас нет достаточных доказательств, чтобы сказать, что истинная средняя высота этого вида растений не превышает 15 дюймов.

Пример 2. Двухвыборочный t-критерий

Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух популяций или нет.

Например, предположим, что исследователи хотят знать, вызывает ли новая обработка топлива изменение среднего пробега на галлон данного автомобиля. Чтобы проверить это, они проводят эксперимент, в ходе которого 12 автомобилей получают новое топливо, а 12 — нет.

Исследователи выполняют двухвыборочный t-критерий со следующими нулевыми и альтернативными гипотезами:

• H ₀ : μ ₁ = μ ₂ (среднее количество миль на галлон между двумя популяциями одинаково)
• H ₁ : μ ₁ ≠ μ ₂ (средний расход миль на галлон между двумя популяциями не равен)

Они выполняют двухвыборочный t-тест в SPSS и получают следующие результаты:

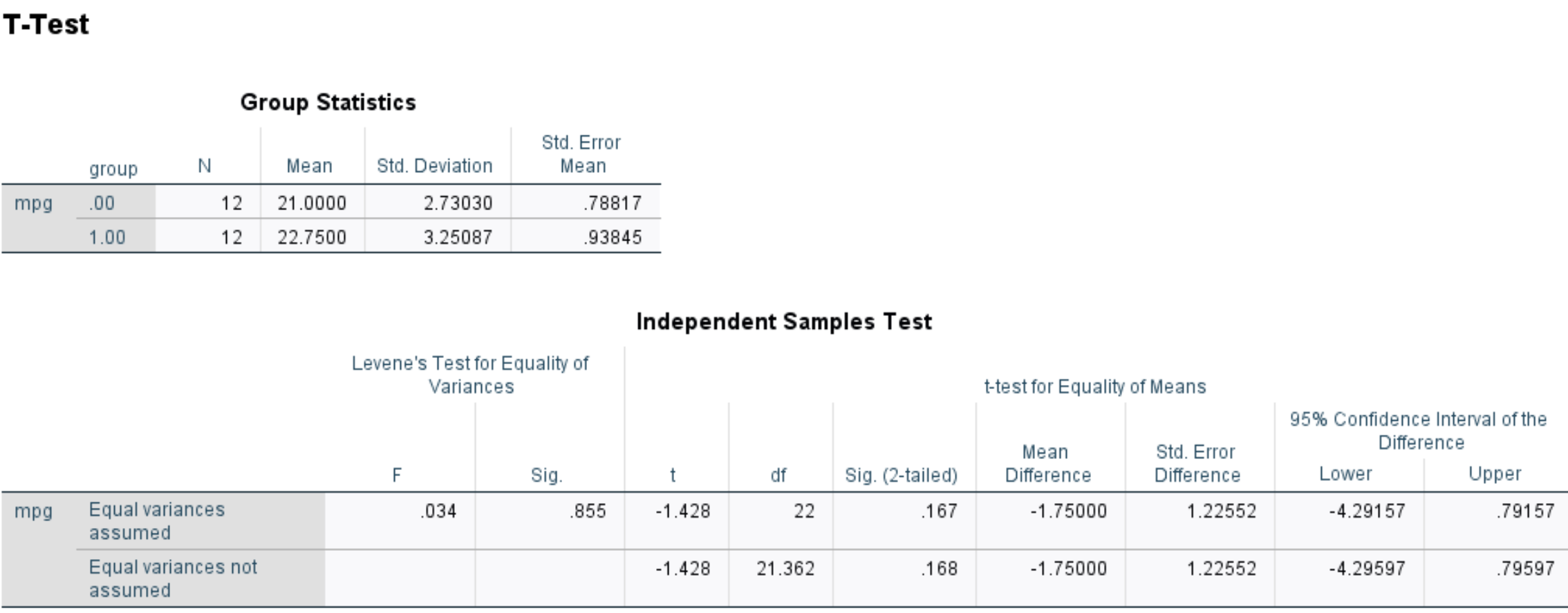
Сиг. Значение (двустороннее) составляет 0,167 .

Это представляет собой двустороннее значение p, которое соответствует значению -1,428 с 22 степенями свободы.

Поскольку значение p теста (0,167) не менее 0,05, мы не можем отвергнуть нулевую гипотезу.

Другими словами, у нас нет достаточных доказательств, чтобы сказать, что истинный средний расход миль на галлон различается между автомобилями, прошедшими обработку, и автомобилями, которые этого не делают.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять различные статистические тесты в SPSS:

Как выполнить одновыборочный t-тест в SPSS
Как выполнить t-тест для двух выборок в SPSS
Как выполнить t-критерий парных выборок в SPSS