Что такое унимодальное распределение? (определение & #038; пример)
Унимодальное распределение — это распределение вероятностей с четким пиком.
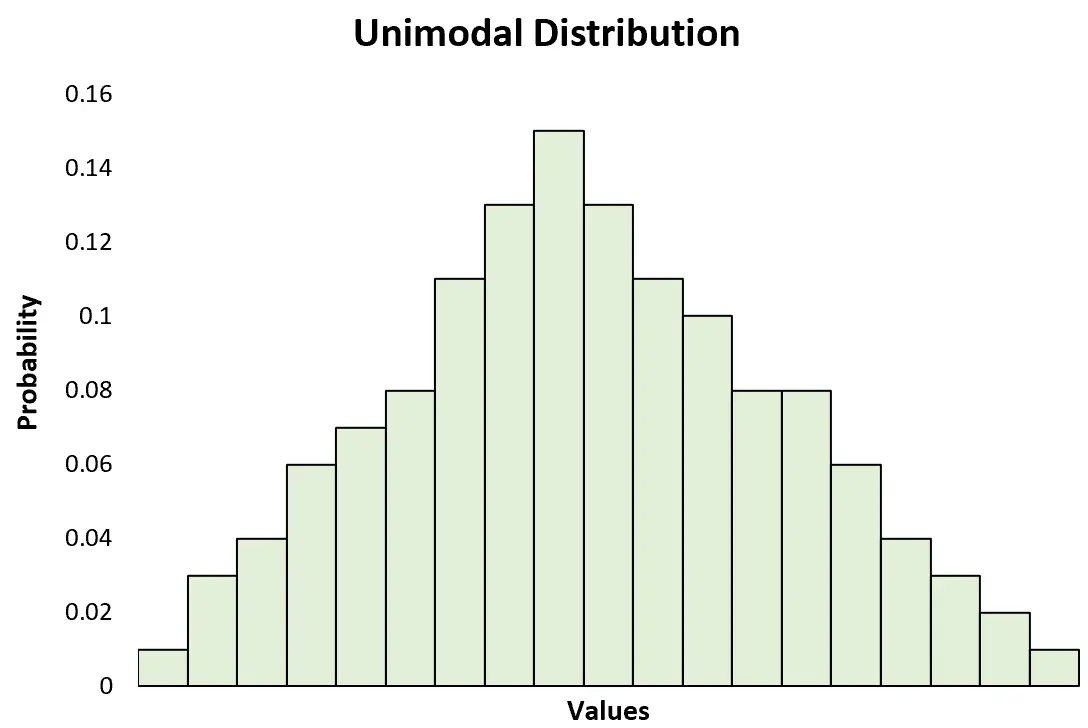
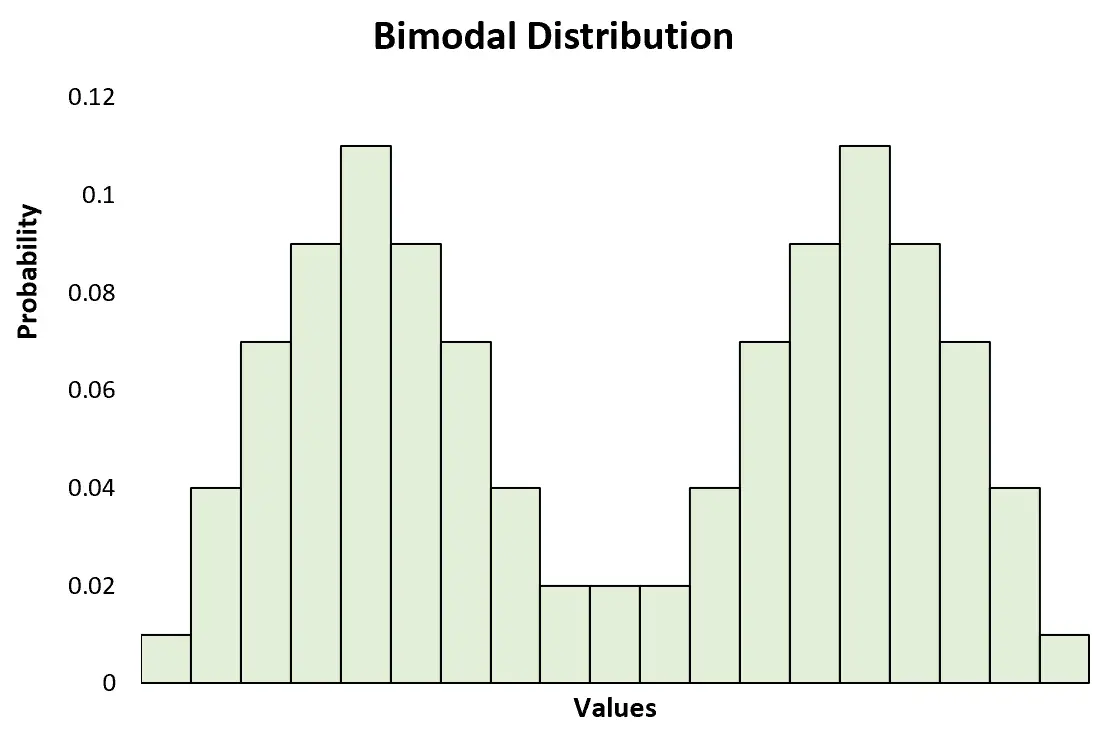
Это контрастирует с бимодальным распределением , которое имеет два четких пика:
Это также контрастирует с мультимодальным распределением , имеющим два или более пиков:
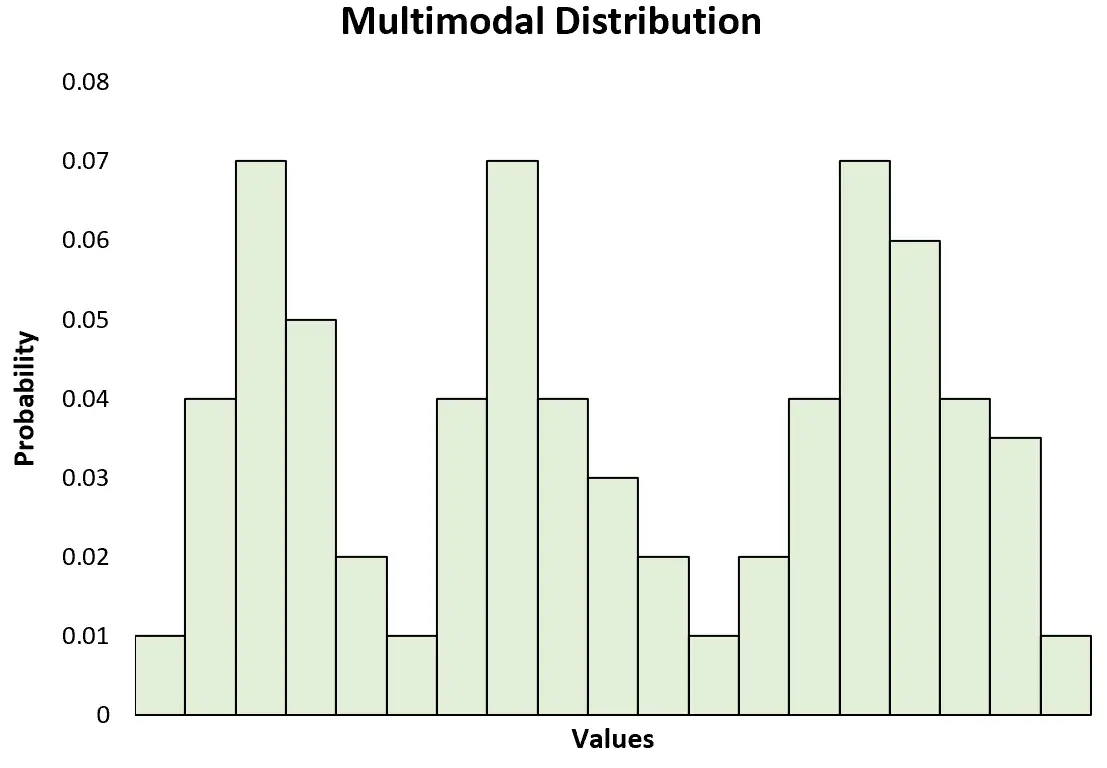
Примечание. Бимодальное распределение — это всего лишь особый тип мультимодального распределения.
Примеры унимодальных распределений
Вот несколько примеров унимодальных распределений на практике.
Пример 1: Вес младенцев при рождении
Хорошо известно, что распределение веса новорожденных соответствует унимодальному распределению, в среднем около 7,5 фунтов. Если мы создадим гистограмму веса детей, мы увидим «пик» на уровне 7,5 фунтов, при этом некоторые дети будут весить больше, а другие — меньше.

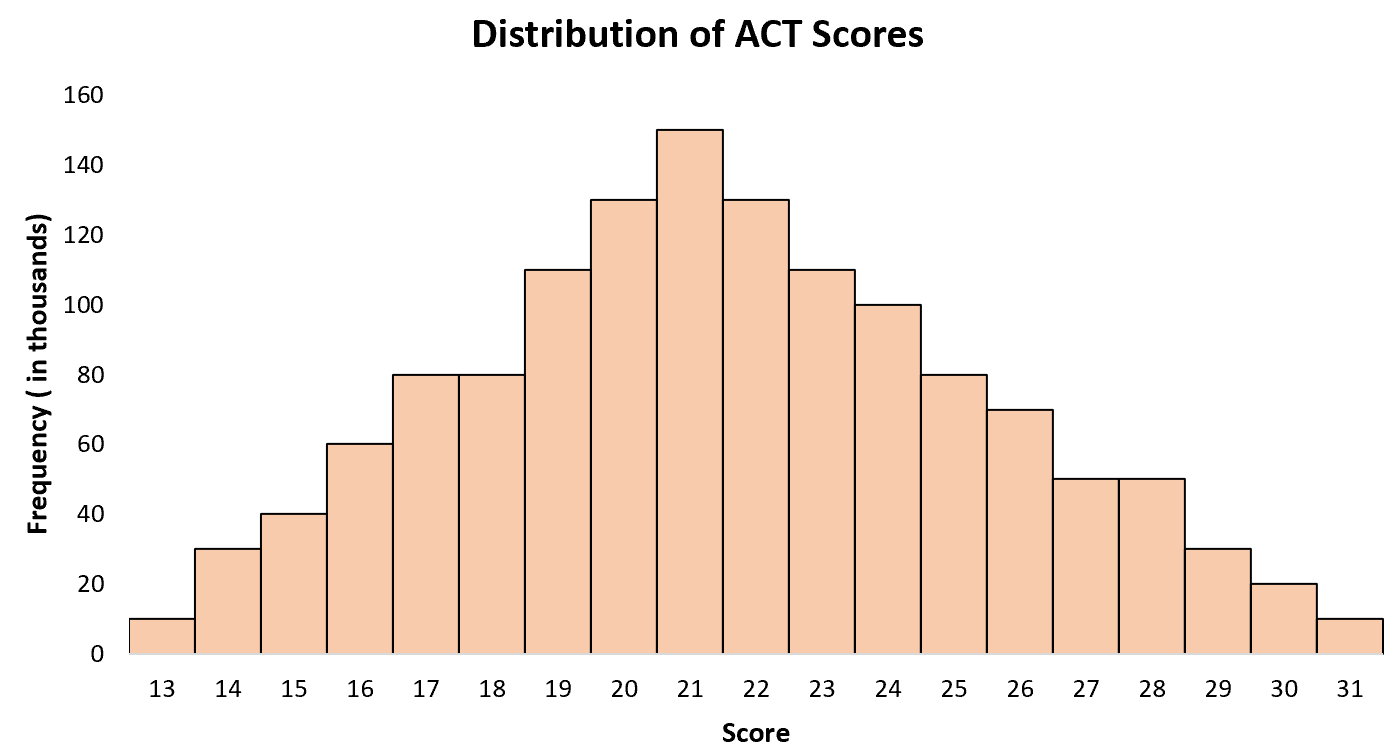
Пример 2: баллы ACT
Средний балл ACT для старшеклассников в США составляет около 21, при этом некоторые ученики набирают меньше, а другие — выше. Если мы создадим гистограмму баллов ACT для всех учащихся в США, мы увидим один «пик» в возрасте 21 года, с более высокими баллами для некоторых учащихся и более низкими баллами для других.
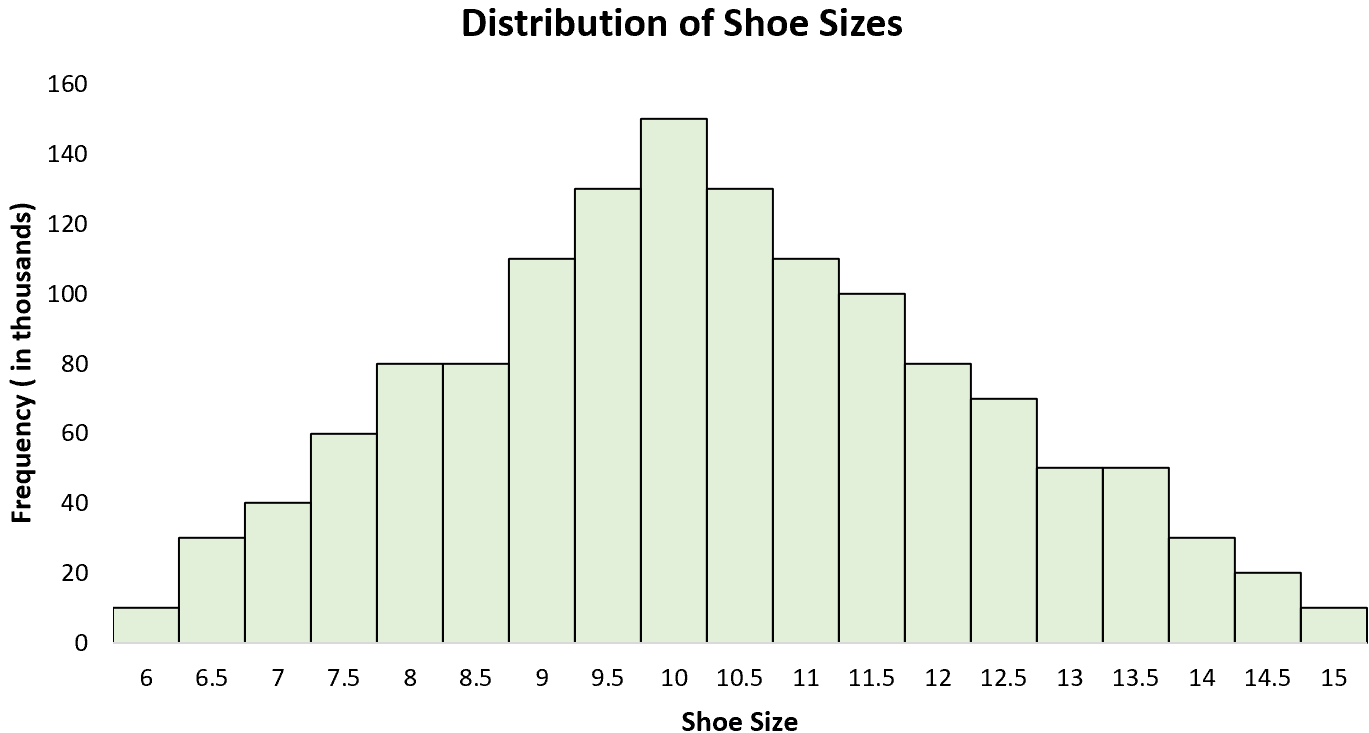
Пример 3: размеры обуви
Распределение размеров мужской обуви представляет собой унимодальное распределение с «пиком» около 10. Если мы создадим гистограмму всех размеров мужской обуви, мы увидим один пик в размере 10, где некоторые мужчины носят обувь большего размера, а другие — большего. размер. Меньший размер.
Унимодальные распределения в статистике
Все следующие распределения вероятностей в статистике являются унимодальными распределениями:
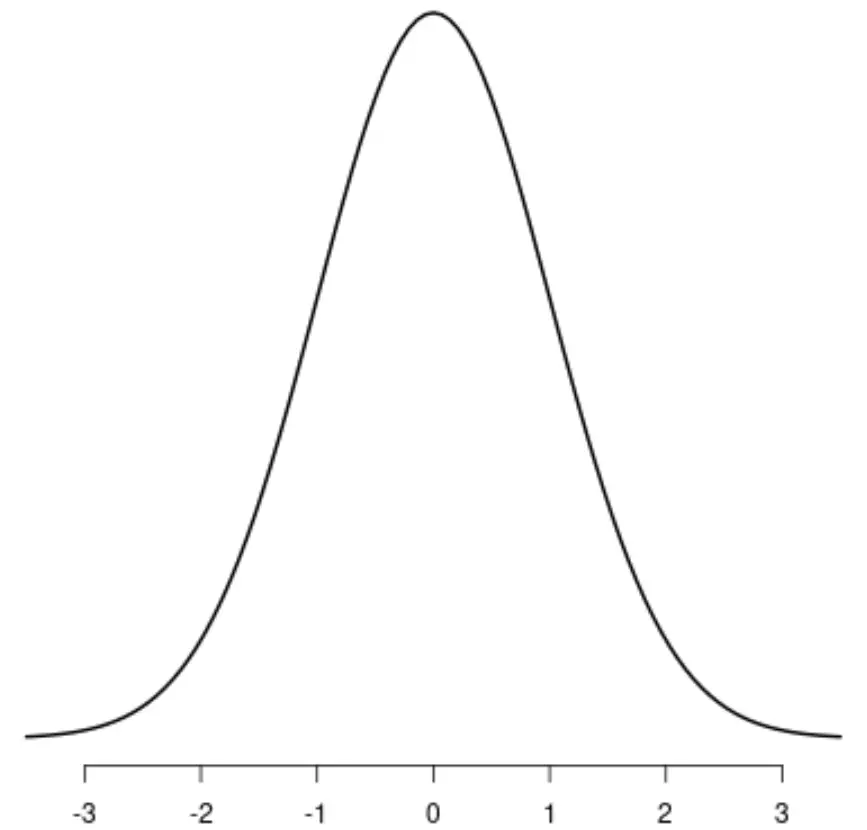
Нормальное распределение
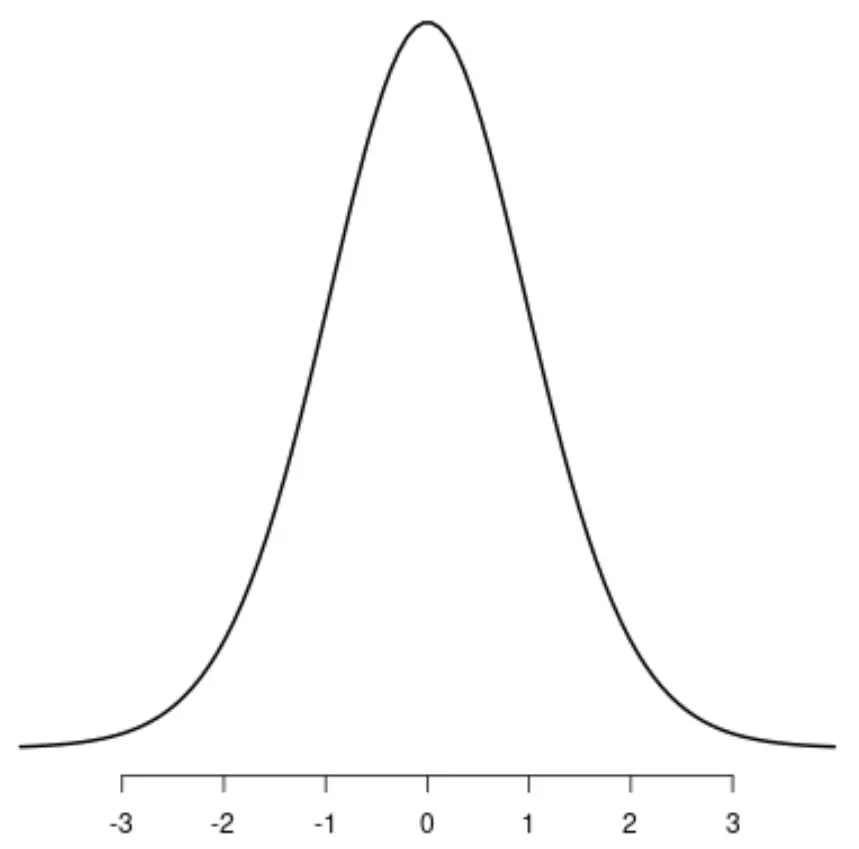
Распределение t
Равномерное распределение

Распределение Коши
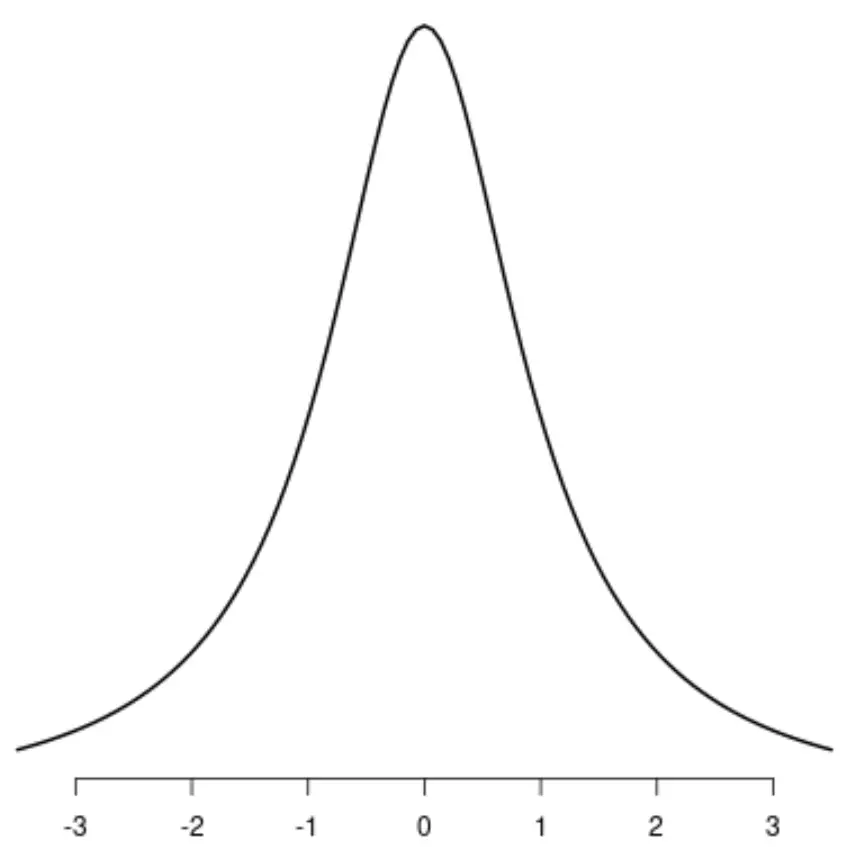
Обратите внимание, что каждое из этих распределений имеет один отчетливый пик.
Как анализировать унимодальные распределения
Мы часто описываем унимодальные распределения, используя три различных меры центральной тенденции :
- Среднее : Среднее значение
- Медиана : медианное значение.
- Режим : значение, которое появляется чаще всего.
В зависимости от асимметрии распределения эти три измерения могут находиться в разных местах.
Распределение с перекосом влево: Среднее < Медиана < Режим
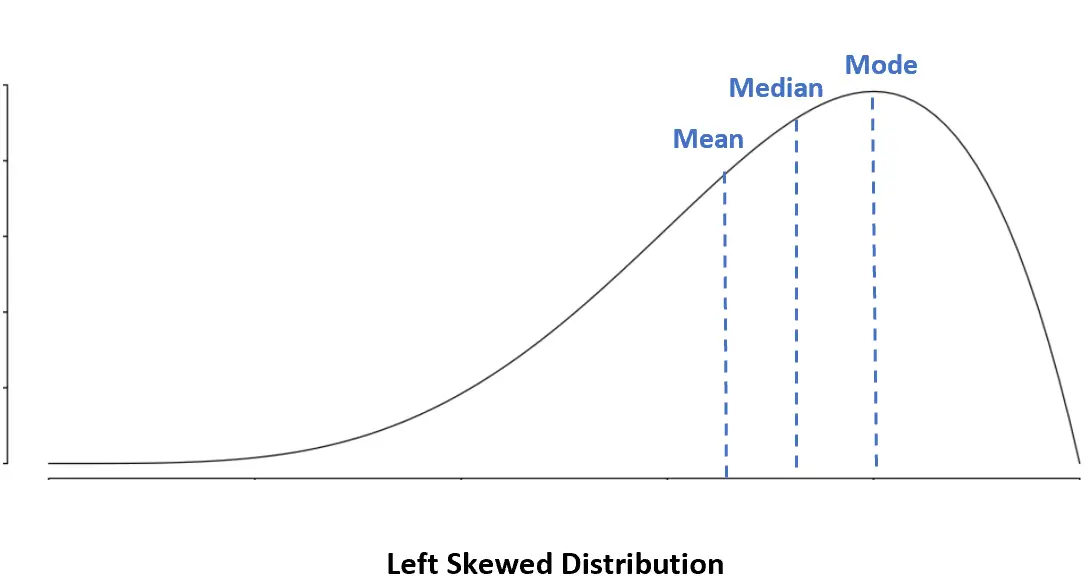
В левом распределении среднее значение меньше медианы.
Правое распределение: Режим < Медиана < Среднее значение
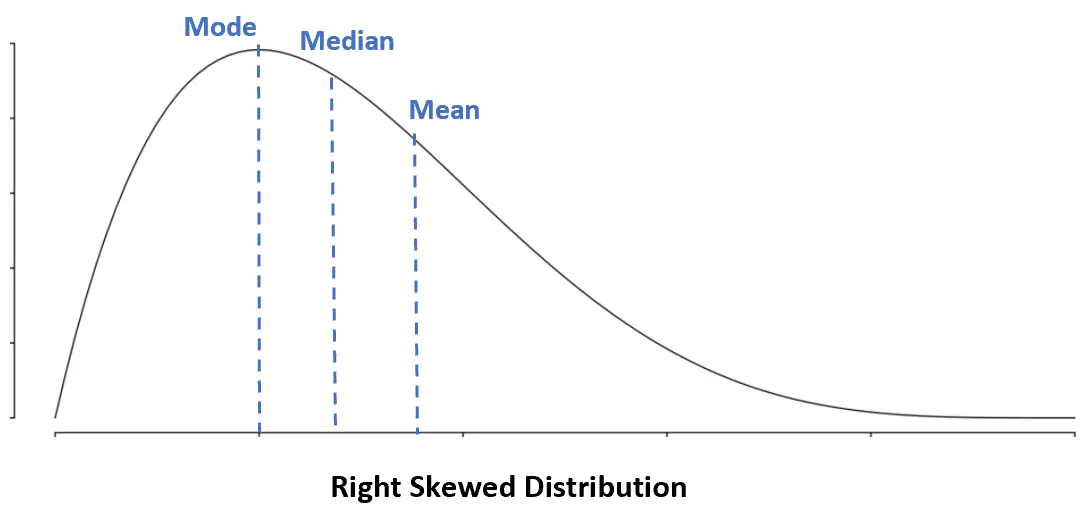
При правостороннем распределении среднее значение больше медианы.
Никакой систематической ошибки: среднее значение = медиана = режим.

В симметричном распределении среднее значение, медиана и мода равны.
Дополнительные ресурсы
Распределения с перекосом влево или вправо
Симметричные распределения: определение + примеры