Условная вероятность (или условная вероятность)

К бенджамин андерсон 6 августа, 2023 Вероятность 0 комментариев

Здесь вы узнаете, что такое условная вероятность (или условная вероятность). Поясним, как рассчитывается условная вероятность, на примере и свойствах этого вида вероятности. Кроме того, вы сможете попрактиковаться, выполняя пошаговые упражнения с условной вероятностью.

Что такое условная вероятность?

Условная вероятность , также называемая условной вероятностью , представляет собой статистическую меру, которая указывает вероятность того, что событие A произойдет, если произойдет другое событие B. То есть условная вероятность P(A|B) относится к вероятности того, что событие A произойдет после того, как событие B уже произошло.

Условная вероятность записывается вертикальной чертой между двумя событиями: P(A|B) и читается: «условная вероятность события A при данном событии B».

Обратите внимание, что значение условной вероятности представляет собой число от 0 до 1. Чем выше условная вероятность, тем больше вероятность того, что событие A произойдет, когда произойдет событие B, но чем ниже условная вероятность, тем менее вероятно, что событие A произойдет. произойдет, когда произойдет событие B.

Формула условной вероятности

Условная вероятность события А при событии В равна вероятности пересечения события А и события В, деленной на вероятность события В.

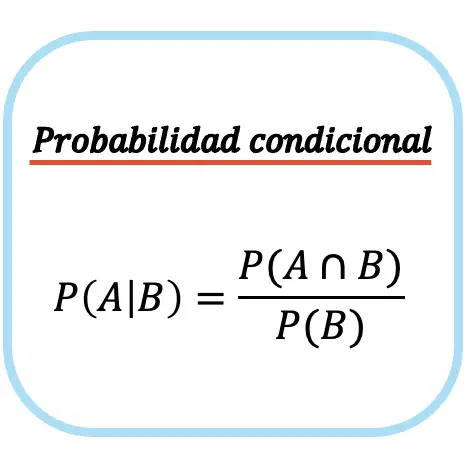
Обратите внимание, что формулу условной вероятности (или условной вероятности) можно использовать только в том случае, если вероятность возникновения безусловного события не равна нулю, т.е. P(B)≠0. Другими словами, возможно ли событие B.

Условную вероятность также можно вычислить по ее обратной величине, т. е. если известно P(B|A), то можно определить P(A|B). Но для этого необходимо применить теорему Байеса, посмотреть, в чем состоит эта теорема, можно здесь:

➤ См.: Что такое теорема Байеса?

Пример условной вероятности

Как только мы увидим, что такое определение и формула условной вероятности, мы шаг за шагом решим пример этого типа вероятности, чтобы полностью понять ее значение.

После сдачи экзамена в классе из 30 учеников были собраны данные, чтобы узнать, сколько учеников учились и сколько сдали экзамен. Результаты представлены в следующей таблице непредвиденных обстоятельств. По собранным данным посчитайте условную вероятность сдачи экзамена, если вы уже учились.

Упражнение на условную вероятность решено

Чтобы получить условную вероятность, мы должны применить формулу, которую мы видели ранее:

$P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}$

Поэтому сначала нам нужно найти вероятность того, что студент учился, учился и сдал экзамен. Чтобы найти вероятность того, что студент учился, нам просто нужно воспользоваться правилом Лапласа, то есть разделить количество обучавшихся студентов на общее количество наблюдений:

$P(\text{estudiado})=\cfrac{23}{30}=0,77$

А вероятность того, что студент учился и сдал экзамен одновременно, мы можем узнать из таблицы непредвиденных обстоятельств, разделив количество студентов, которые учились и сдали экзамен, на общее количество:

$P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63$

Таким образом, вероятность того, что студент сдаст экзамен, если он учился, равна:

$\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}$

Условная вероятность зависимых и независимых событий

В этом разделе мы увидим, какова связь между условной вероятностью и зависимыми и независимыми событиями (или зависимыми и независимыми событиями). Потому что, хотя это разные понятия, эти два типа событий связаны с условной вероятностью.

Два события (или явления) независимы, если вероятность их возникновения не зависит друг от друга. В таком случае пересечение двух событий эквивалентно произведению вероятности каждого события в отдельности. И, следовательно, формула условной вероятности упрощается:

$P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)$

Короче говоря, если события A и B независимы, условная вероятность события A при данном событии B точно равна вероятности возникновения события A.

С другой стороны, когда два события зависимы, это означает, что вероятность одного события зависит от вероятности другого события. Следовательно, когда два события А и В зависимы, условная вероятность события А при данном событии В отличается от вероятности наступления события А.

$P(A|B)\neq P(A)$

Решенные упражнения на условную вероятность

Упражнение 1

Мы знаем, что в мешке, полном шариков, половина оранжевого цвета, а другая половина зеленого. Кроме того, треть всех шаров оранжевого цвета и при этом отмечена знаком. Какова вероятность того, что когда вы вытащите оранжевый шар, он получит сигнал?

Посмотреть решение

Для решения упражнения необходимо применить условную формулу вероятности, которая есть:

$P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}$

Постановка задачи говорит нам, что половина пакета — апельсины. Следовательно, теоретическая вероятность подобрать оранжевый шар равна 50%.

$P(\text{naranja})=\cfrac{1}{2}=0,5$

С другой стороны, мы знаем, что треть общего числа являются оранжевыми шарами и имеют сигнал, поэтому вероятность получения оранжевого шара с сигналом равна:

$P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33$

Наконец, подставляем вычисленные вероятности в формулу условной вероятности, чтобы найти ее значение:

$\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}$

Таким образом, вероятность выпадения шара с сигналом, если он оранжевый, составляет 66%.

Упражнение 2

Если у нас в коробке шесть синих ручек и три черных ручки, вычислите вероятность вытянуть одну синюю ручку и вероятность вытянуть подряд две синие ручки.

Посмотреть решение

Чтобы определить вероятность того, что вы однажды возьмете в руки синюю ручку, просто воспользуйтесь законом Лапласа:

$P(\text{azul})=\cfrac{6}{6+3}=0,67$

Задача также требует от нас знать вероятность взять в руки две синие ручки подряд, то есть условную вероятность взять в руки синюю ручку, если мы уже брали синюю ручку раньше.

Если мы нарисуем синюю ручку, то у нас менее благоприятный случай, но в сумме тоже на одну ручку меньше. Таким образом, условная вероятность равна:

$P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63$

Упражнение 3

Какова условная вероятность того, что на игральной кости выпадет число 4, если при подбрасывании монеты выпадет решка?

Посмотреть решение

Для решения этого упражнения необходимо принять во внимание теорию условной вероятности, поскольку события «получение числа 4 при бросании игральной кости» и «получение орла при бросании монеты» независимы. Поэтому нет необходимости использовать формулу условной вероятности, но выполняется следующее равенство:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})$

Итак, чтобы найти условную вероятность, просто используйте правило Лапласа:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167$

Упражнение 4

Был изучен финансовый год 25 компаний в стране и то, как меняются цены их акций в зависимости от экономического результата года. Вы можете увидеть собранные данные в следующей таблице непредвиденных обстоятельств:

Насколько вероятно, что цена акций компании вырастет, если за последний год она получила прибыль?

Посмотреть решение

В упражнении нас спрашивают об условной вероятности того, что акции вырастут при условии, что компания достигла положительного экономического результата. Итак, чтобы вычислить эту вероятность, мы должны использовать формулу условной вероятности:

$P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}$

Поэтому мы сначала вычисляем вероятность того, что компания получит прибыль, а во-вторых, вероятность того, что компания получит экономическую прибыль при увеличении своей цены за акцию:

$P(\text{beneficio})=\cfrac{14}{25}=0,56$

$P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4$

А затем подставляем найденные значения в формулу и вычисляем условную вероятность:

$\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}$

Свойства условной вероятности

Свойства условной вероятности, или условной вероятности, заключаются в следующем:

Сумма условной вероятности события А при условии события В плюс условная вероятность дополнительного события А при условии события В равна единице.

$P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1$

Если событие A является подмножеством события B, событие A всегда произойдет, когда событие B истинно. Таким образом, условная вероятность события А при условии события Б в этих случаях равна 1.

$B\subseteq A \ \longrightarrow \ P(A|B)=1$

Для двух разных событий всегда выполняется следующее равенство относительно условной вероятности:

$P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое условная вероятность?

Формула условной вероятности

Пример условной вероятности

Условная вероятность зависимых и независимых событий

Решенные упражнения на условную вероятность

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Свойства условной вероятности

Об авторе

бенджамин андерсон

Добавить комментарий