Как выполнить робастную регрессию в r (шаг за шагом)

Робастная регрессия — это метод, который мы можем использовать в качестве альтернативы обычной регрессии наименьших квадратов, когда в наборе данных, с которым мы работаем, есть выбросы или влиятельные наблюдения .

Чтобы выполнить надежную регрессию в R, мы можем использовать функцию rlm() из пакета MASS , которая использует следующий синтаксис:

В следующем пошаговом примере показано, как выполнить робастную регрессию в R для заданного набора данных.

Шаг 1. Создайте данные

Во-первых, давайте создадим поддельный набор данных для работы:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

Шаг 2. Выполните регрессию обычных наименьших квадратов

Далее давайте применим обычную модель регрессии наименьших квадратов и создадим график стандартизированных остатков .

На практике мы часто рассматриваем любой стандартизированный остаток, абсолютное значение которого превышает 3, как выброс.

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

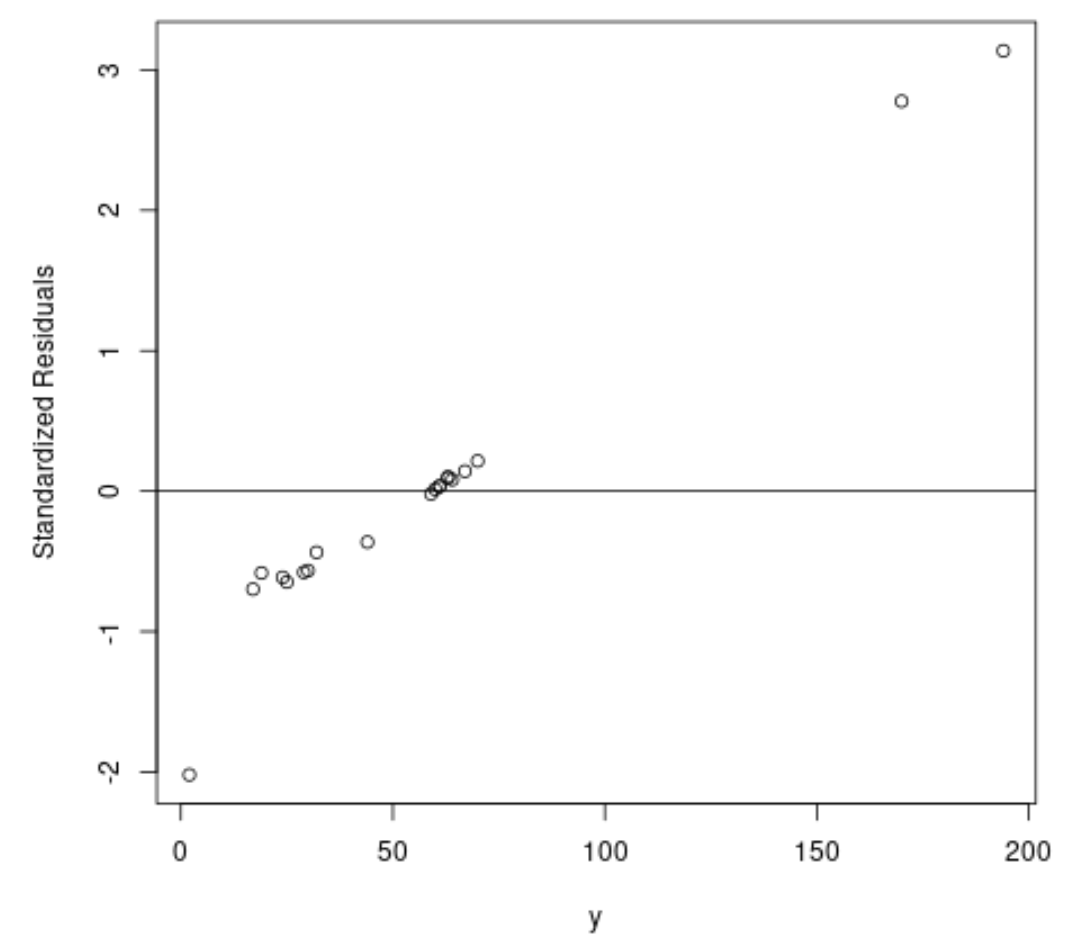
На графике мы видим, что есть два наблюдения со стандартизированными остатками около 3.

Это указывает на то, что в наборе данных есть два потенциальных выброса, и поэтому вместо этого мы могли бы извлечь выгоду из надежной регрессии.

Шаг 3. Выполните робастную регрессию

Далее давайте воспользуемся функцией rlm() , чтобы подогнать надежную модель регрессии:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Чтобы определить, обеспечивает ли эта робастная регрессионная модель лучшее соответствие данным по сравнению с моделью OLS, мы можем рассчитать остаточную стандартную ошибку каждой модели.

Остаточная стандартная ошибка (RSE) — это способ измерения стандартного отклонения остатков в регрессионной модели. Чем ниже значение CSR, тем лучше модель соответствует данным.

Следующий код показывает, как рассчитать RSE для каждой модели:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

Мы видим, что RSE модели устойчивой регрессии намного ниже, чем у обычной модели регрессии наименьших квадратов, что говорит нам о том, что модель устойчивой регрессии обеспечивает лучшее соответствие данным.

Дополнительные ресурсы

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить полиномиальную регрессию в R