Что такое факторный дисперсионный анализ? (определение & #038; пример)
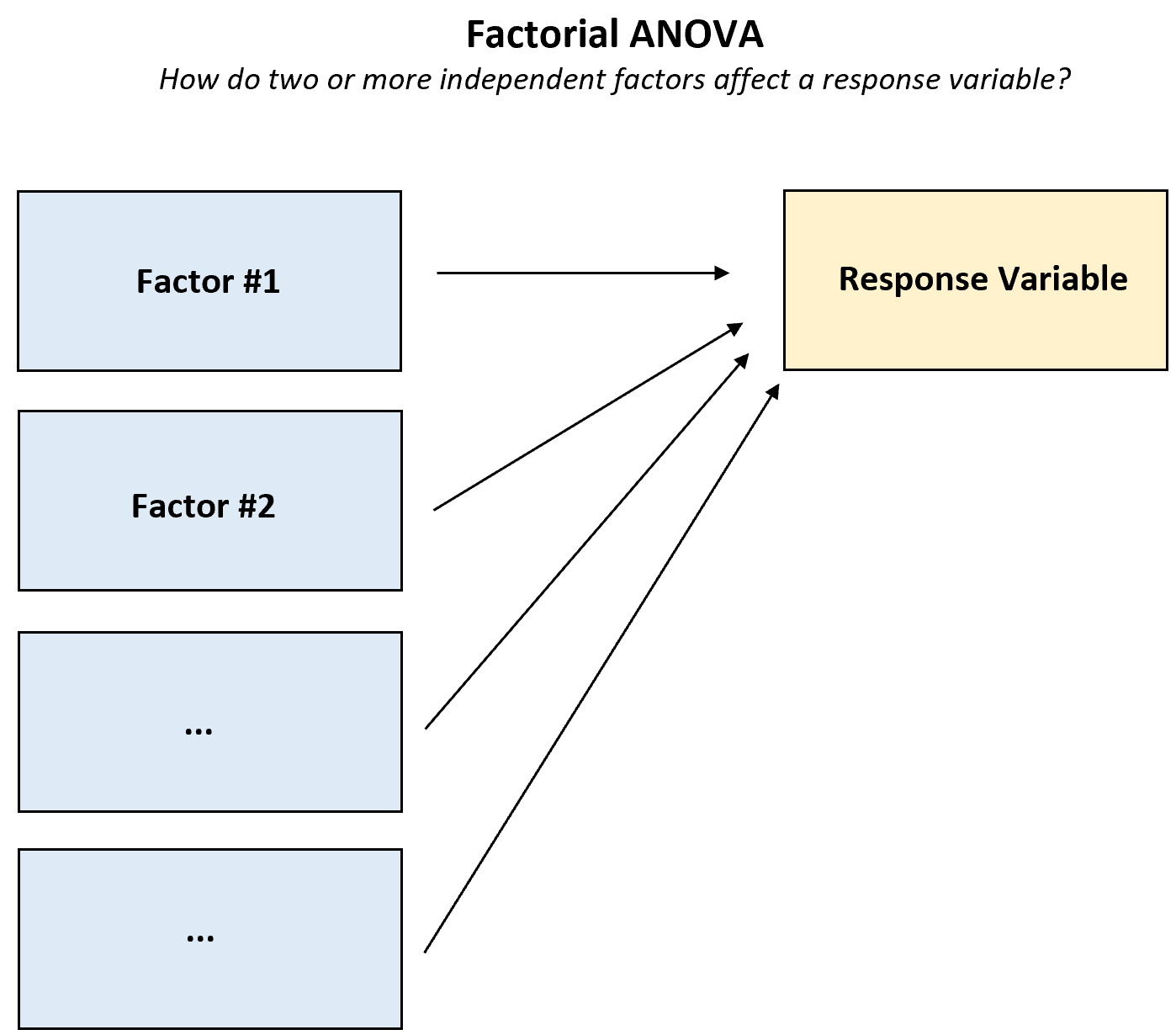
Факториальный дисперсионный анализ — это любой дисперсионный анализ («дисперсионный анализ»), в котором используются два или более независимых фактора и одна переменная отклика.
Этот тип дисперсионного анализа следует использовать всякий раз, когда вы хотите понять, как два или более фактора влияют на переменную ответа и существует ли эффект взаимодействия между факторами на переменную ответа.
В этом руководстве представлено несколько примеров ситуаций, в которых можно использовать факторный дисперсионный анализ, а также пошаговый пример выполнения факторного дисперсионного анализа.
Примечание. Двусторонний дисперсионный анализ — это разновидность факторного дисперсионного анализа.
Примеры использования факторного ANOVA
Факторный дисперсионный анализ можно использовать в каждой из следующих ситуаций.
Пример 1: Рост растений
Ботаник хочет понять, как воздействие солнца и частота полива влияют на рост растений. Она сажает 100 семян и дает им расти в течение трех месяцев при различных условиях пребывания на солнце и частоты полива. Через три месяца она записывает высоту каждого растения.
В данном случае он имеет следующие переменные:
- Переменная ответа: рост растений
- Факторы: пребывание на солнце, частота полива.
И она хотела бы ответить на следующие вопросы:
- Влияет ли пребывание на солнце на рост растений?
- Влияет ли частота полива на рост растений?
- Существует ли эффект взаимодействия между пребыванием на солнце и частотой полива?
Для этого анализа она может использовать факторный дисперсионный анализ, поскольку хочет понять, как два фактора влияют на одну переменную ответа.
Пример 2: Результаты экзамена
Профессор хочет понять, как время занятий и метод обучения влияют на результаты экзамена. Он использует два разных метода обучения и два разных времени обучения (рано утром и рано днем) и записывает средние экзаменационные баллы каждого студента в конце семестра.
В данном случае он имеет следующие переменные:
- Переменная ответа: оценка экзамена
- Факторы: метод обучения, время обучения.
И он хотел бы ответить на следующие вопросы:
- Влияет ли метод обучения на результаты экзамена?
- Влияет ли время обучения на результаты экзаменов?
- Существует ли эффект взаимодействия между методом обучения и временем обучения?
Для этого анализа он может использовать факторный дисперсионный анализ, поскольку хочет понять, как два фактора влияют на одну переменную ответа.
Пример 3: Годовой доход
Экономист собирает данные, чтобы понять, как уровень образования (аттестат средней школы, диплом колледжа, высшее образование), семейное положение (холост, разведен, женат) и регион (Север, Восток, Юг, Запад) влияют на годовой доход.
В данном случае он имеет следующие переменные:
- Переменная ответа: годовой доход
- Факторы: уровень образования, семейное положение, регион.
И он хотел бы ответить на следующие вопросы:
- Влияет ли уровень образования на доходы?
- Влияет ли семейное положение на доходы?
- Влияет ли регион на доход?
- Существует ли эффект взаимодействия между этими тремя независимыми факторами?
Для этого анализа он может использовать факторный дисперсионный анализ, поскольку хочет понять, как три фактора влияют на одну переменную ответа.
Пошаговый пример факторного дисперсионного анализа
Ботаник хочет знать, влияет ли воздействие солнечного света и частота полива на рост растений. Она сажает 40 семян и дает им расти в течение двух месяцев при различных условиях солнечного света и частоты полива. Через два месяца она записывает высоту каждого растения.
Результаты показаны ниже:

Видно, что в каждой комбинации условий выращивалось по пять растений.
Например, пять растений выращивались при ежедневном поливе и без солнечного света, а их высота через два месяца составила 4,8 дюйма, 4,4 дюйма, 3,2 дюйма, 3,9 дюйма и 4,4 дюйма:

Ботаник использует эти данные для выполнения факторного дисперсионного анализа в Excel и получает следующий результат:
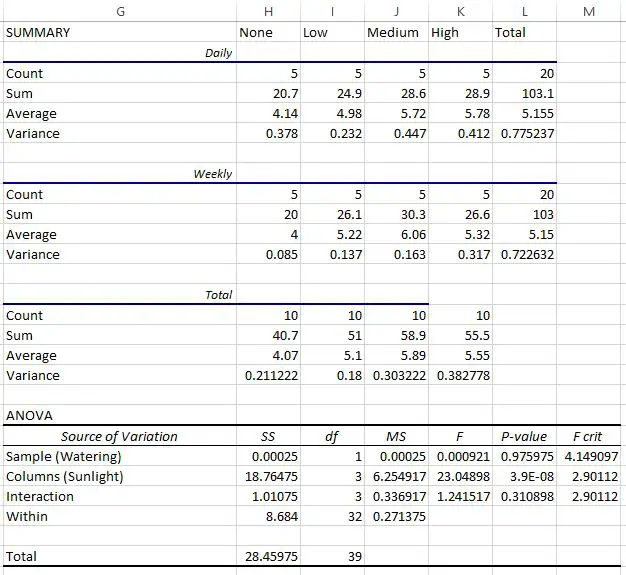
В последней таблице показан результат факторного дисперсионного анализа:
- Значение p для взаимодействия между частотой полива и пребыванием на солнце составило 0,310898 . Это не является статистически значимым на уровне альфа 0,05.
- Значение p для частоты полива составило 0,975975 . Это не является статистически значимым на уровне альфа 0,05.
- Значение p для пребывания на солнце составило 3,9E-8 (0,000000039) . Это статистически значимо на уровне альфа 0,05.
Можно сделать вывод, что воздействие солнечного света является единственным фактором, оказывающим статистически значимое влияние на рост растений.
Мы также можем заключить, что нет эффекта взаимодействия между воздействием солнца и частотой полива и что частота полива не оказывает статистически значимого влияния на рост растений. растения.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о моделях ANOVA:
Введение в однофакторный дисперсионный анализ
Введение в двусторонний дисперсионный анализ
Введение в повторяющиеся измерения ANOVA
Различия между ANOVA, ANCOVA, MANOVA и MANCOVA