Полное руководство: факторный дизайн 2×2
Факторный план 2 × 2 — это тип экспериментального плана, который позволяет исследователям понять влияние двух независимых переменных (каждая с двумя уровнями ) на одну зависимую переменную.
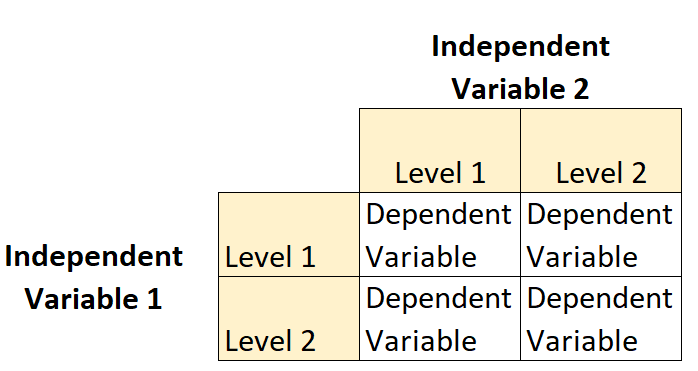
Например, предположим, что ботаник хочет понять влияние солнечного света (низкого или высокого) и частоты полива (ежедневно или еженедельно) на рост определенного вида растений.
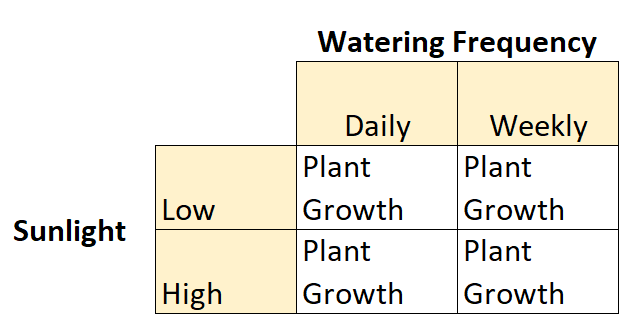
Это пример факторного плана 2×2, поскольку имеется две независимые переменные, каждая из которых имеет два уровня:
- Независимая переменная № 1: Солнечный свет
- Уровни: низкий, высокий
- Независимая переменная №2: Частота полива.
- Уровни: ежедневно, еженедельно.
И есть зависимая переменная: рост растений.
Цель факторного плана 2 × 2
Факторный план 2×2 позволяет проанализировать следующие эффекты:
Основные эффекты: это влияние, которое одна независимая переменная оказывает на зависимую переменную.
Например, в нашем предыдущем сценарии мы могли бы проанализировать следующие основные эффекты:
- Основное влияние солнечного света на рост растений.
- Мы можем найти средний рост всех растений, получавших мало солнечного света.
- Мы можем найти средний рост всех растений, получивших много солнечного света.
- Основное влияние частоты полива на рост растений.
- Мы можем найти средний рост всех растений, поливаемых ежедневно.
- Мы можем найти средний рост всех растений, поливаемых каждую неделю.
Эффекты взаимодействия: они возникают, когда влияние одной независимой переменной на зависимую переменную зависит от уровня другой независимой переменной.
Например, в нашем предыдущем сценарии мы могли бы проанализировать следующие эффекты взаимодействия:
- Зависит ли влияние солнечного света на рост растений от частоты полива?
- Зависит ли влияние частоты полива на рост растений от солнечного света?
Визуализация основных эффектов и эффектов взаимодействия
Когда мы используем факторный план 2 × 2, мы часто отображаем средние значения, чтобы лучше понять влияние, которое независимые переменные оказывают на зависимую переменную.
Например, рассмотрим следующий график:
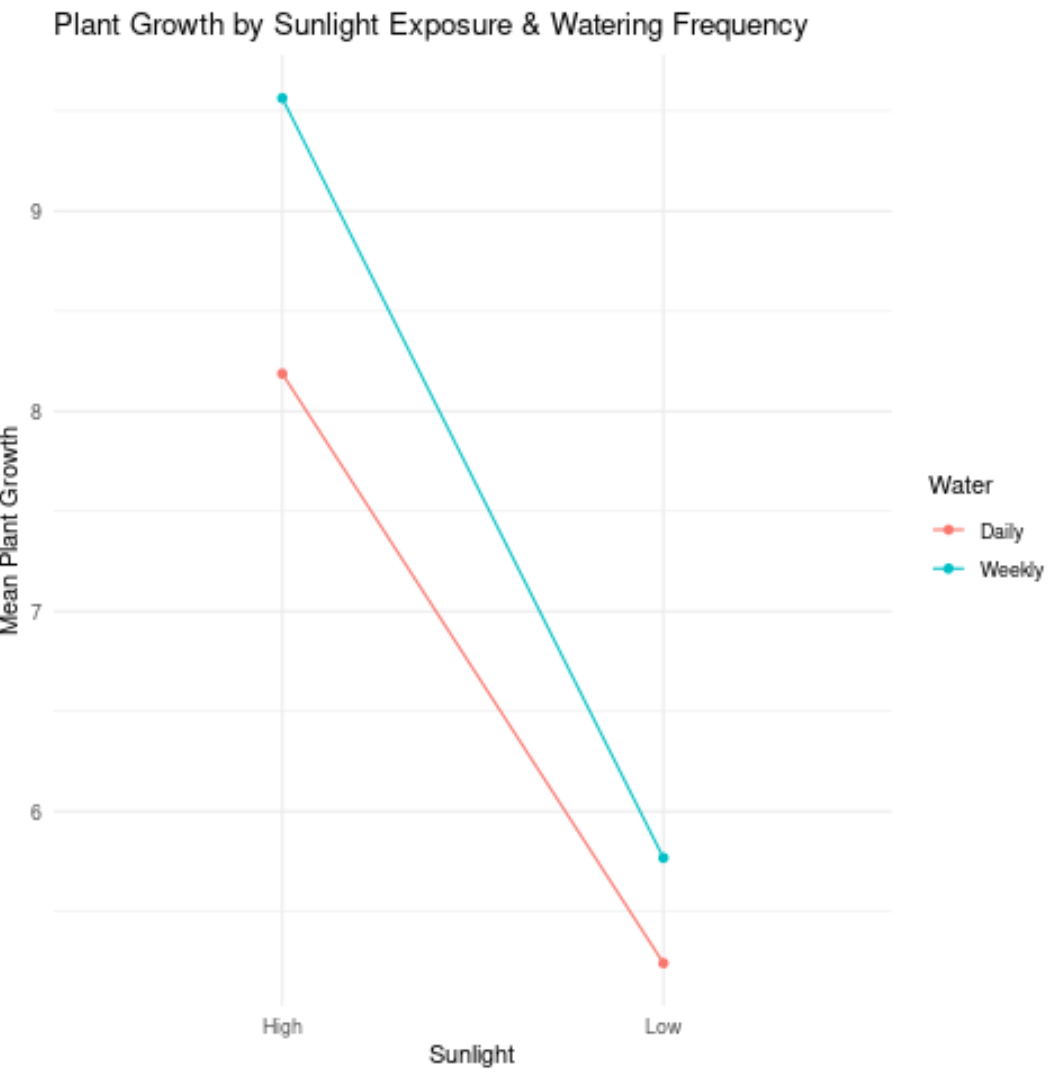
Вот как интерпретировать значения на графике:
- Средний рост растений, получавших интенсивный солнечный свет и ежедневный полив, составил около 8,2 дюйма.
- Средний рост растений, получавших яркий солнечный свет и еженедельный полив, составлял около 9,6 дюймов.
- Средний рост растений, получавших мало солнца и ежедневный полив, составлял около 5,3 дюйма.
- Средний рост растений, получавших низкое солнце и еженедельный полив, составил около 5,8 дюймов.
Чтобы определить, существует ли эффект взаимодействия между двумя независимыми переменными, просто проверьте, параллельны ли линии или нет:
- Если две линии графика параллельны, эффекта взаимодействия нет.
- Если две линии графика не параллельны, возникает эффект взаимодействия.
На предыдущем графике две линии были примерно параллельны, поэтому, вероятно, нет эффекта взаимодействия между частотой полива и пребыванием на солнце.
Однако рассмотрим следующий сюжет:
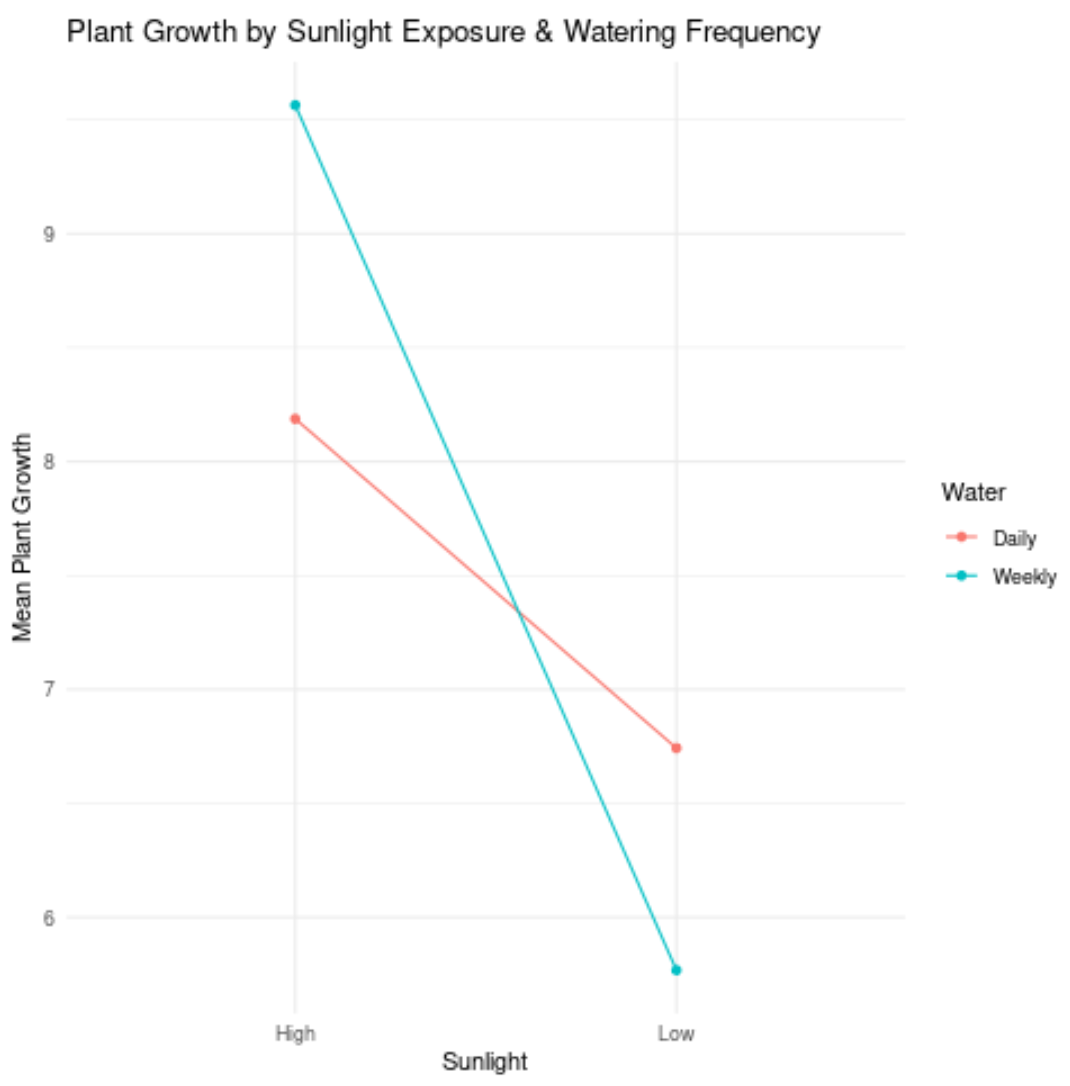
Две линии вовсе не параллельны (на самом деле они пересекаются!), что указывает на то, что между ними, вероятно, существует эффект взаимодействия.
Например, это означает, что влияние солнечного света на рост растений зависит от частоты полива.
Другими словами, солнечный свет и частота полива не влияют независимо на рост растений. Скорее, существует эффект взаимодействия между двумя независимыми переменными.
Как анализировать факторный план 2×2
Построение графика средних значений — это визуальный способ проверить влияние независимых переменных на зависимую переменную.
Однако мы также можем выполнить двусторонний дисперсионный анализ , чтобы формально проверить, имеют ли независимые переменные статистически значимую связь с зависимой переменной.
Например, следующий код показывает, как выполнить двусторонний дисперсионный анализ для нашего гипотетического фабричного сценария в R:
#make this example reproducible set. seeds (0) df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ), water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ), growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2), rnorm(15, 10, 3))) #fit the two-way ANOVA model model <- aov(growth ~ sunlight * water, data = df) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) sunlight 1 52.5 52.48 8.440 0.00525 ** water 1 31.6 31.59 5.081 0.02813 * sunlight:water 1 12.8 12.85 2.066 0.15620 Residuals 56 348.2 6.22 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Вот как интерпретировать результат ANOVA:
- Значение p, связанное с солнечным светом, составляет 0,005 . Поскольку это число меньше 0,05, это означает, что воздействие солнечного света оказывает статистически значимое влияние на рост растений.
- Значение p, связанное с водой, составляет 0,028 . Поскольку этот показатель меньше 0,05, это означает, что частота полива также оказывает статистически значимое влияние на рост растений.
- Значение p для взаимодействия солнечного света и воды составляет 0,156 . Поскольку этот показатель составляет не менее 0,05, это означает отсутствие эффекта взаимодействия солнечного света и воды.
Дополнительные ресурсы
Полное руководство: факторный план 2 × 3
Что такое уровни независимой переменной?
Независимые или зависимые переменные
Что такое факторный дисперсионный анализ?