Коэффициент фи: определение и примеры
Коэффициент Фи (иногда называемый среднеквадратичным коэффициентом непредвиденности ) является мерой связи между двумя двоичными переменными.
Для таблицы 2×2, заданной для двух случайных величин x и y :

Коэффициент Фи можно рассчитать следующим образом:
Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)
Пример: расчет коэффициента Фи
Предположим, мы хотим знать, связан ли пол с предпочтением той или иной политической партии. Мы берем простую случайную выборку из 25 избирателей и спрашиваем их об их предпочтениях в отношении политических партий. В следующей таблице представлены результаты опроса:
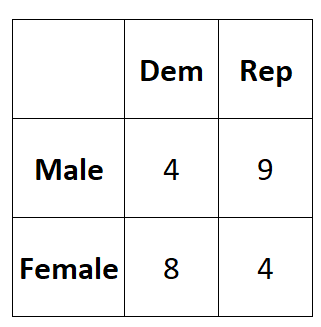
Мы можем рассчитать коэффициент Фи между двумя переменными следующим образом:
Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72) / √ 24336 = -0,3589
Примечание. Мы также могли бы рассчитать это с помощью калькулятора коэффициентов Фи.
Как интерпретировать коэффициент Фи
Подобно коэффициенту корреляции Пирсона, коэффициент Фи принимает значения от -1 до 1, где:
- -1 указывает на совершенно отрицательную связь между двумя переменными.
- 0 указывает на отсутствие связи между двумя переменными.
- 1 указывает на совершенно положительную связь между двумя переменными.
В общем, чем дальше коэффициент Фи от нуля, тем сильнее связь между двумя переменными.
Другими словами, чем дальше коэффициент Фи от нуля, тем больше свидетельств какой-то систематической закономерности между двумя переменными.
Дополнительные ресурсы
Руководство по коэффициенту корреляции Пирсона
Руководство по точному тесту Фишера
Руководство по тесту независимости хи-квадрат