Как использовать фиктивные переменные в регрессионном анализе
Линейная регрессия — это метод, который мы можем использовать для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Обычно мы используем линейную регрессию с количественными переменными . Иногда называемые «числовыми» переменными, это переменные, которые представляют собой измеримую величину. Примеры включают в себя:
- Количество квадратных футов в доме
- Численность населения города
- Возраст человека
Однако иногда мы хотим использовать категориальные переменные в качестве переменных-предсказателей. Это переменные, которые принимают имена или метки и могут относиться к категориям. Примеры включают в себя:
- Цвет глаз (например, «голубой», «зеленый», «карий»)
- Пол (например, «мужчина», «женщина»)
- Семейное положение (например, «женат», «холост», «разведен»)
При использовании категориальных переменных не имеет смысла просто присваивать значения типа 1, 2, 3 таким значениям, как «синий», «зеленый» и «коричневый», потому что не имеет смысла говорить этот зеленый цвет двойной. такой же красочный, как синий или коричневый, в три раза красочнее синего.
Вместо этого решение состоит в использовании фиктивных переменных . Это переменные, которые мы создаем специально для регрессионного анализа и которые принимают одно из двух значений: ноль или единицу.
Фиктивные переменные: числовые переменные, используемые в регрессионном анализе для представления категориальных данных, которые могут принимать только одно из двух значений: ноль или одно.
Количество фиктивных переменных, которые нам нужно создать, равно k -1, где k — количество различных значений, которые может принимать категориальная переменная.
Следующие примеры иллюстрируют, как создавать фиктивные переменные для разных наборов данных.
Пример 1. Создайте фиктивную переменную только с двумя значениями.
Предположим, у нас есть следующий набор данных и мы хотим использовать пол и возраст для прогнозирования дохода :
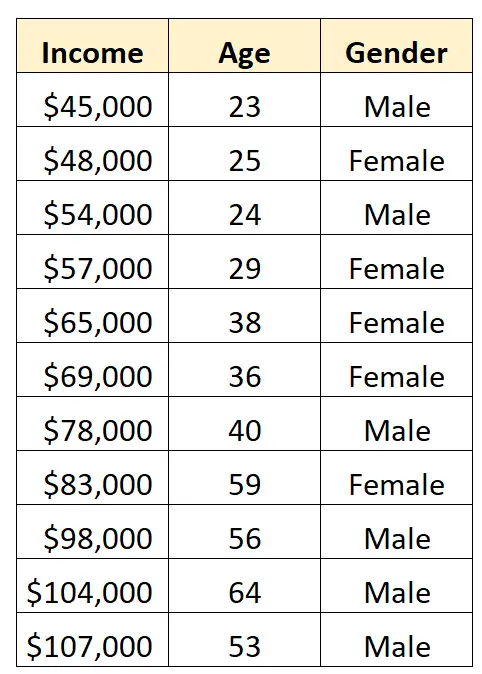
Чтобы использовать пол в качестве предикторной переменной в регрессионной модели, нам нужно преобразовать его в фиктивную переменную.
Поскольку на данный момент это категориальная переменная, которая может принимать два разных значения («Мужской» или «Женский»), мы просто создаем k -1 = 2-1 = 1 фиктивную переменную.
Чтобы создать эту фиктивную переменную, мы можем выбрать одно из значений («Мужской» или «Женский») для обозначения 0, а другое — для обозначения 1.
В общем, мы обычно обозначаем наиболее часто встречающееся значение цифрой 0, что в этом наборе данных будет «Мужским».
Итак, вот как преобразовать пол в фиктивную переменную:
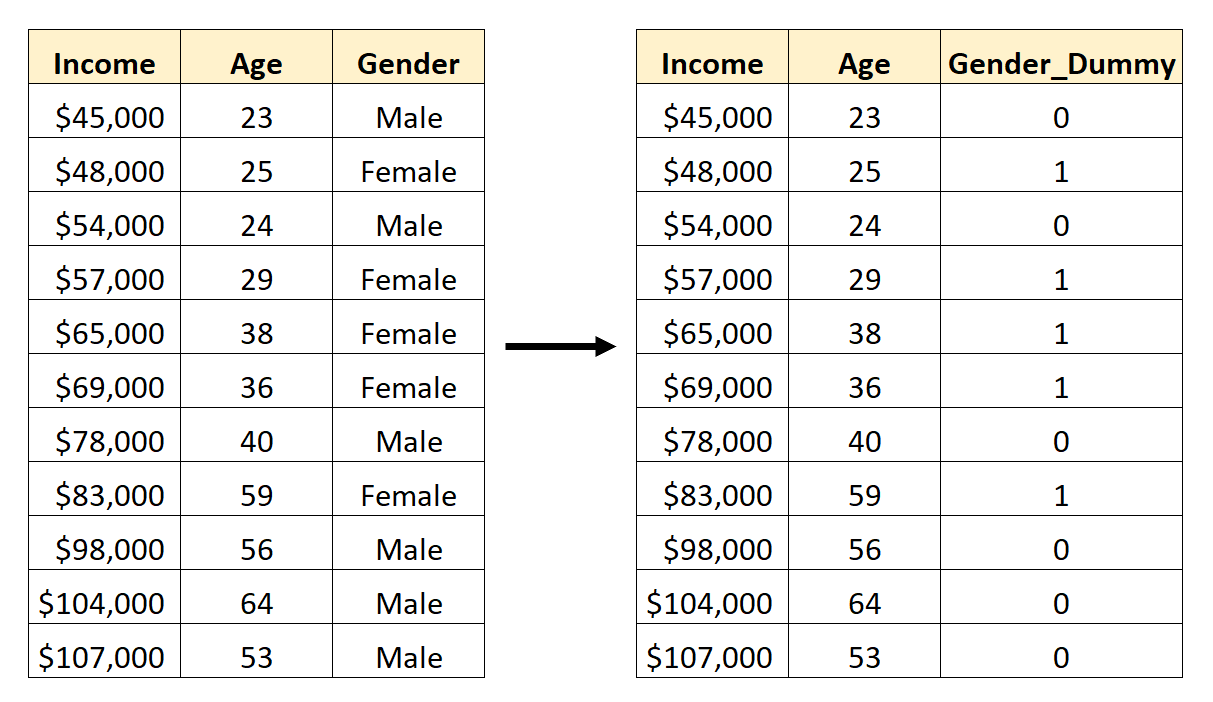
Затем мы могли бы использовать Age и Gender_Dummy в качестве переменных-предикторов в регрессионной модели.
Пример 2. Создайте фиктивную переменную с несколькими значениями.
Допустим, у нас есть следующий набор данных и мы хотим использовать семейное положение и возраст для прогнозирования дохода :

Чтобы использовать семейное положение в качестве предикторной переменной в регрессионной модели, нам необходимо преобразовать его в фиктивную переменную.
Поскольку на данный момент это категориальная переменная, которая может принимать три разных значения («холост», «женат» или «разведен»), нам нужно создать k -1 = 3-1 = 2 фиктивных переменных.
Чтобы создать эту фиктивную переменную, мы можем оставить «Single» в качестве базового значения, поскольку оно встречается чаще всего. Итак, вот как мы преобразуем семейное положение в фиктивные переменные:

Затем мы могли бы использовать Возраст , Женат и Разведен в качестве переменных-предсказателей в регрессионной модели.
Как интерпретировать результаты регрессии с фиктивными переменными
Предположим, мы подбираем модель множественной линейной регрессии , используя набор данных из предыдущего примера с Age , Married и Divorced в качестве переменных-предикторов и доходом в качестве переменной ответа.
Вот результат регрессии:
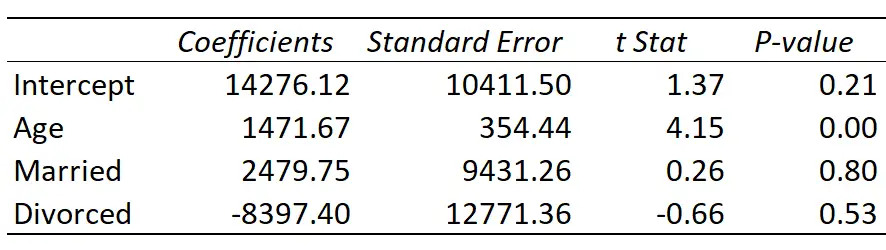
Подобранная линия регрессии определяется как:
Доход = 14 276,21 + 1 471,67*(Возраст) + 2 479,75*(Женат) – 8 397,40*(Разведен)
Мы можем использовать это уравнение, чтобы найти расчетный доход человека в зависимости от его возраста и семейного положения. Например, человек в возрасте 35 лет, женатый, будет иметь расчетный доход в размере 68 264 долларов США :
Доход = 14 276,21 + 1 471,67*(35) + 2 479,75*(1) – 8 397,40*(0) = 68 264 долларов США.
Вот как интерпретировать коэффициенты регрессии в таблице:
- Перехват: Перехват представляет собой средний доход одного человека в возрасте нулевого возраста. Очевидно, что у вас не может быть нулевых лет, поэтому нет смысла интерпретировать перехват сам по себе в этой конкретной регрессионной модели.
- Возраст: каждый год увеличения возраста связан со средним увеличением дохода на 1471,67 доллара. Поскольку значение p (0,00) меньше 0,05, возраст является статистически значимым предиктором дохода.
- Женатый: женатый человек зарабатывает в среднем на 2479,75 доллара больше, чем одинокий. Поскольку значение p (0,80) составляет не менее 0,05, эта разница не является статистически значимой.
- Разведен: Разведенный человек зарабатывает в среднем на 8 397,40 доллара меньше, чем одинокий человек. Поскольку значение p (0,53) составляет не менее 0,05, эта разница не является статистически значимой.
Поскольку обе фиктивные переменные не были статистически значимыми, мы могли бы исключить семейное положение как предиктор из модели, поскольку оно, по-видимому, не увеличивает прогностическую ценность дохода.
Дополнительные ресурсы
Качественные и количественные переменные
Ловушка фиктивной переменной
Как читать и интерпретировать таблицу регрессии
Объяснение значений P и статистической значимости