Как использовать fitdistr() в r для подбора дистрибутивов

Вы можете использовать функцию fitdistr() из пакета MASS в R, чтобы оценить параметры распределения путем максимизации функции правдоподобия.

Эта функция использует следующий базовый синтаксис:

fitdistr(x, Densentfun, …)

Золото:

• x : числовой вектор, представляющий значения распределения
• плотное развлечение : распределение для оценки параметров

Обратите внимание, что аргумент плотное развлечение принимает следующие имена потенциального распределения: бета , Коши , хи-квадрат , экспоненциальное , гамма , геометрическое , логнормальное , логистическое , отрицательное биномиальное , нормальное , Пуассона , t и Вейбулла .

В следующем примере показано, как использовать функцию fitdistr() на практике.

Пример. Как использовать функцию fitdistr() для подбора распределений в R.

Предположим, мы используем функцию rnorm() в R для генерации вектора из 200 значений, который соответствует нормальному распределению:

 #make this example reproducible
set. seeds (1)

#generate sample of 200 observations that follows normal dist with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

Мы можем использовать функцию hist() для создания гистограммы для визуализации распределения значений данных:

 hist(data, col=' steelblue ')

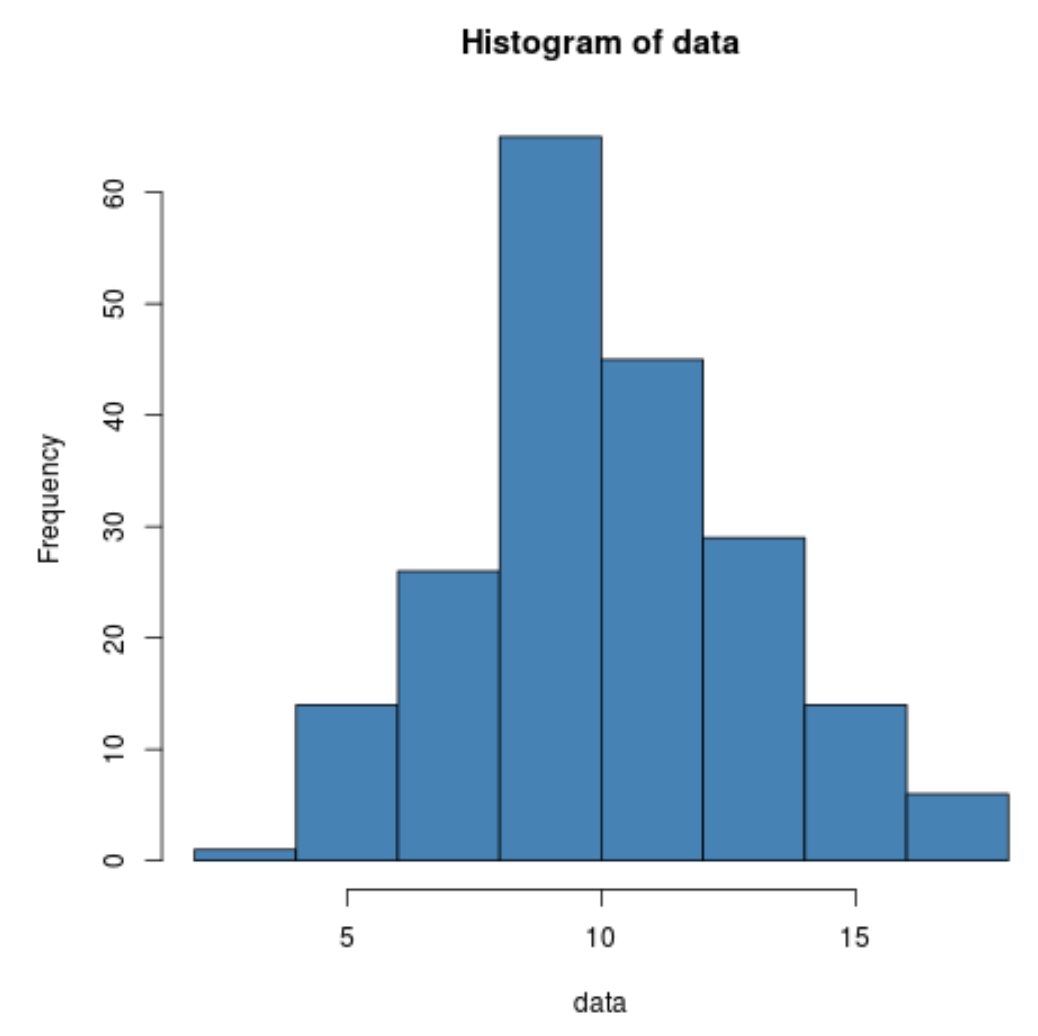
Мы видим, что данные действительно распределены нормально.

Затем мы можем использовать функцию fitdistr() для оценки параметров этого распределения:

 library (MASS)

#estimate parameters of distribution
fitdistr(data, “ normal ”)

      mean sd    
  10.1066189 2.7803148 
 (0.1965979) (0.1390157)

Функция fitdistr() оценивает, что вектор значений соответствует нормальному распределению со средним значением 10,1066189 и стандартным отклонением 2,7803148 .

Эти значения не должны вызывать удивления, поскольку мы сгенерировали данные с помощью функции rnorm() со средним значением 10 и стандартным отклонением 3.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:

Как построить нормальное распределение в R
Как создать нормальное распределение в R
Как выполнить тест Шапиро-Уилка на нормальность в R