Как выполнить тест уайта в sas
Тест Уайта используется для определения наличия гетероскедастичности в регрессионной модели.
Гетероскедастичность относится к неравномерной дисперсии остатков на разных уровнях переменной отклика в регрессионной модели, что нарушает одно из ключевых предположений линейной регрессии о том, что остатки одинаково разбросаны на каждом уровне переменной отклика.
В этом руководстве объясняется, как выполнить тест Уайта в SAS, чтобы определить, является ли гетероскедастичность проблемой в данной регрессионной модели.
Пример: тест белого в SAS
Предположим, мы хотим подогнать модель множественной линейной регрессии, которая использует количество часов, потраченных на обучение, и количество сданных практических экзаменов для прогнозирования итоговой оценки студента на экзамене:
Оценка экзамена = β 0 + β 1 (часы) + β 2 (подготовительные экзамены)
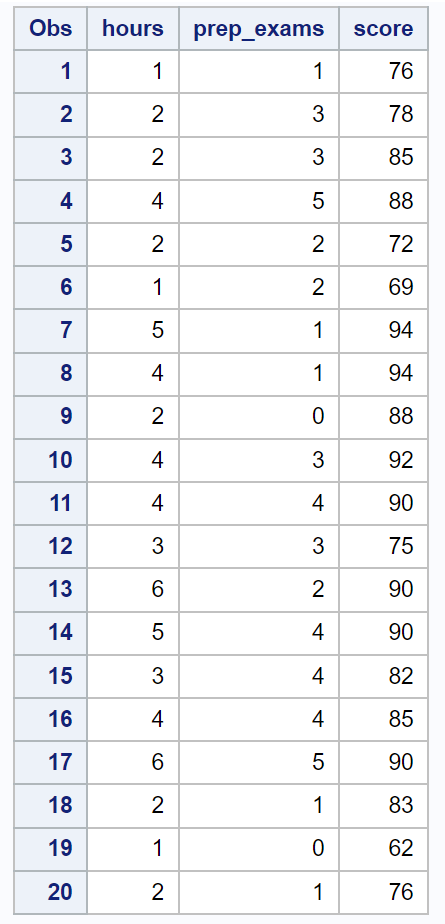
Сначала мы будем использовать следующий код, чтобы создать набор данных, содержащий эту информацию для 20 студентов:
/*create dataset*/ data exam_data; input hours prep_exams score; datalines ; 1 1 76 2 3 78 2 3 85 4 5 88 2 2 72 1 2 69 5 1 94 4 1 94 2 0 88 4 3 92 4 4 90 3 3 75 6 2 90 5 4 90 3 4 82 4 4 85 6 5 90 2 1 83 1 0 62 2 1 76 ; run ; /*view dataset*/ proc print data =exam_data;
Далее мы будем использовать proc reg, чтобы соответствовать этой модели множественной линейной регрессии, а также опцию спецификации для выполнения теста Уайта на гетероскедастичность:
/*fit regression model and perform White's test*/
proc reg data =exam_data;
model score = hours prep_exams / spec ;
run ;
quit ;
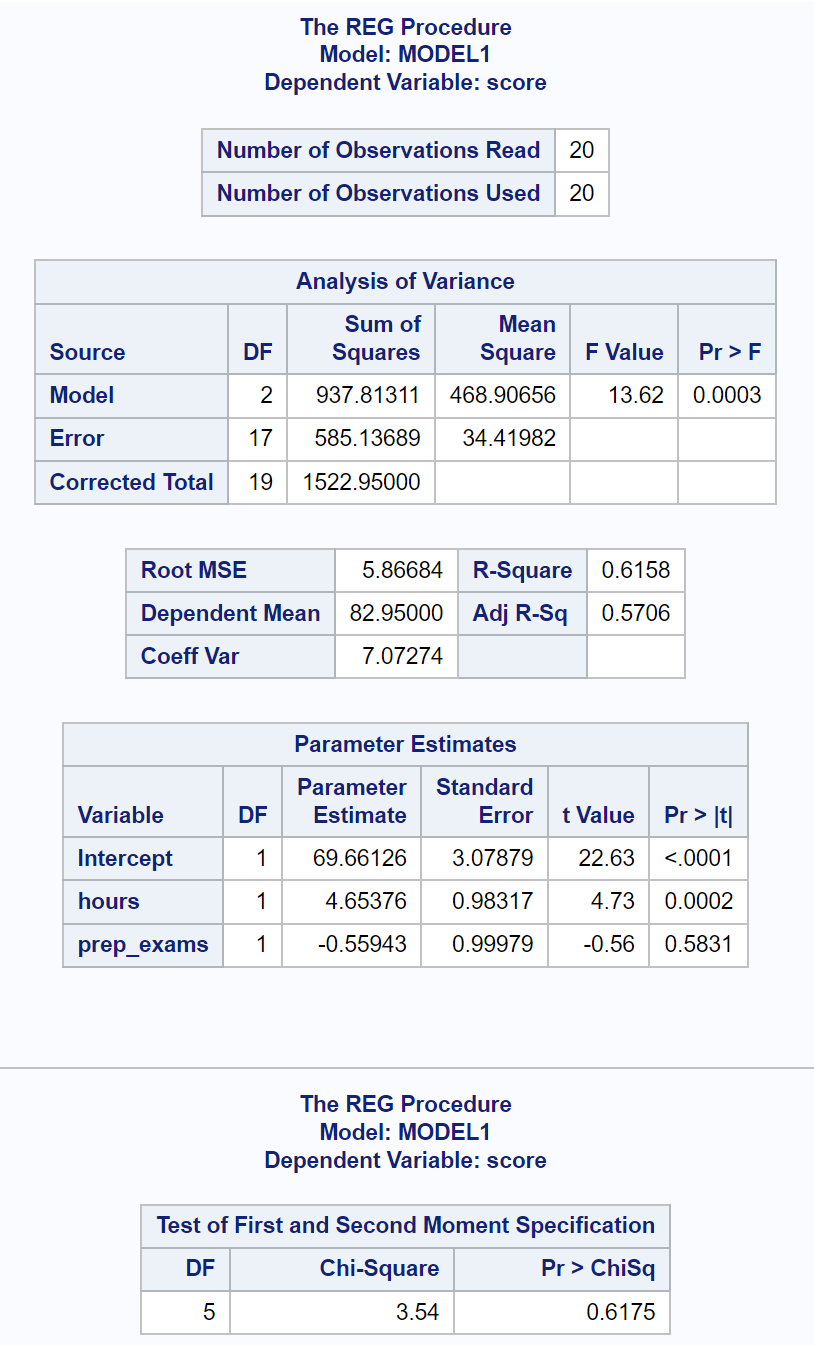
Последняя таблица результатов показывает результаты теста Уайта.
Из этой таблицы мы видим, что статистика теста Хи-квадрат равна 3,54 , а соответствующее значение p составляет 0,6175 .
Тест Уайта использует следующие нулевые и альтернативные гипотезы:
- Нуль (H 0 ) : Гетероскедастичность отсутствует.
- Альтернатива ( HA ): присутствует гетероскедастичность.
Поскольку значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что гетероскедастичность присутствует в регрессионной модели.
Таким образом, можно безопасно интерпретировать стандартные ошибки оценок коэффициентов в сводной таблице регрессии.
Что делать дальше
Если вам не удастся отвергнуть нулевую гипотезу теста Уайта, то гетероскедастичности нет и вы можете приступить к интерпретации результата исходной регрессии.
Однако если вы отклоните нулевую гипотезу, это означает, что в данных присутствует гетероскедастичность. В этом случае стандартные ошибки, отображаемые в выходной таблице регрессии, могут быть недостоверными.
Существует несколько распространенных способов решения этой проблемы, в том числе:
1. Преобразуйте переменную ответа. Вы можете попытаться выполнить преобразование переменной ответа.
Например, вы можете использовать переменную ответа журнала вместо исходной переменной ответа.
Как правило , логарифм переменной отклика является эффективным способом устранения гетероскедастичности.
Другое распространенное преобразование — использование квадратного корня из переменной ответа.
2. Используйте взвешенную регрессию. Этот тип регрессии присваивает вес каждой точке данных на основе дисперсии ее подобранного значения.
Это придает малый вес точкам данных с более высокими дисперсиями, уменьшая их остаточные квадраты.
Использование соответствующих весов позволяет устранить проблему гетероскедастичности.