Что считается хорошим или плохим остаточным участком?

В регрессионном анализе график остатков — это тип графика, который отображает подобранные значения модели регрессии по оси X и остатки модели по оси Y.

При визуальном осмотре остаточного макета мы обычно обращаем внимание на две вещи, чтобы определить, является ли макет «хорошим» или «плохим»:

1. Показывают ли остатки четкую тенденцию?

• На «хорошем» графике остатков остатки не показывают четкой тенденции.
• На «плохом» графике остатков остатки имеют некоторый тип рисунка, например кривую или волну. Это указывает на то, что использованная нами регрессионная модель не обеспечивает должного соответствия данным.

2. Систематически ли увеличиваются или уменьшаются дисперсии остатков?

• На «хорошем» графике остатков остатки случайным образом разбросаны вокруг нуля без систематического увеличения или уменьшения дисперсии.
• На «плохом» графике остатков дисперсия остатков систематически увеличивается или уменьшается.

Если остаточный график имеет оценку «хорошо», это означает, что мы можем доверять результатам регрессионной модели и можно безопасно интерпретировать коэффициенты модели.

Однако если остаточный график имеет оценку «плохо», это означает, что результаты модели ненадежны, и нам необходимо подогнать к данным другую модель регрессии.

Следующие примеры объясняют, как на практике интерпретировать «хорошие» и «плохие» графики остатков.

Пример 1: «хороший» остаточный след

Предположим, мы подбираем регрессионную модель и получаем следующий остаточный график:

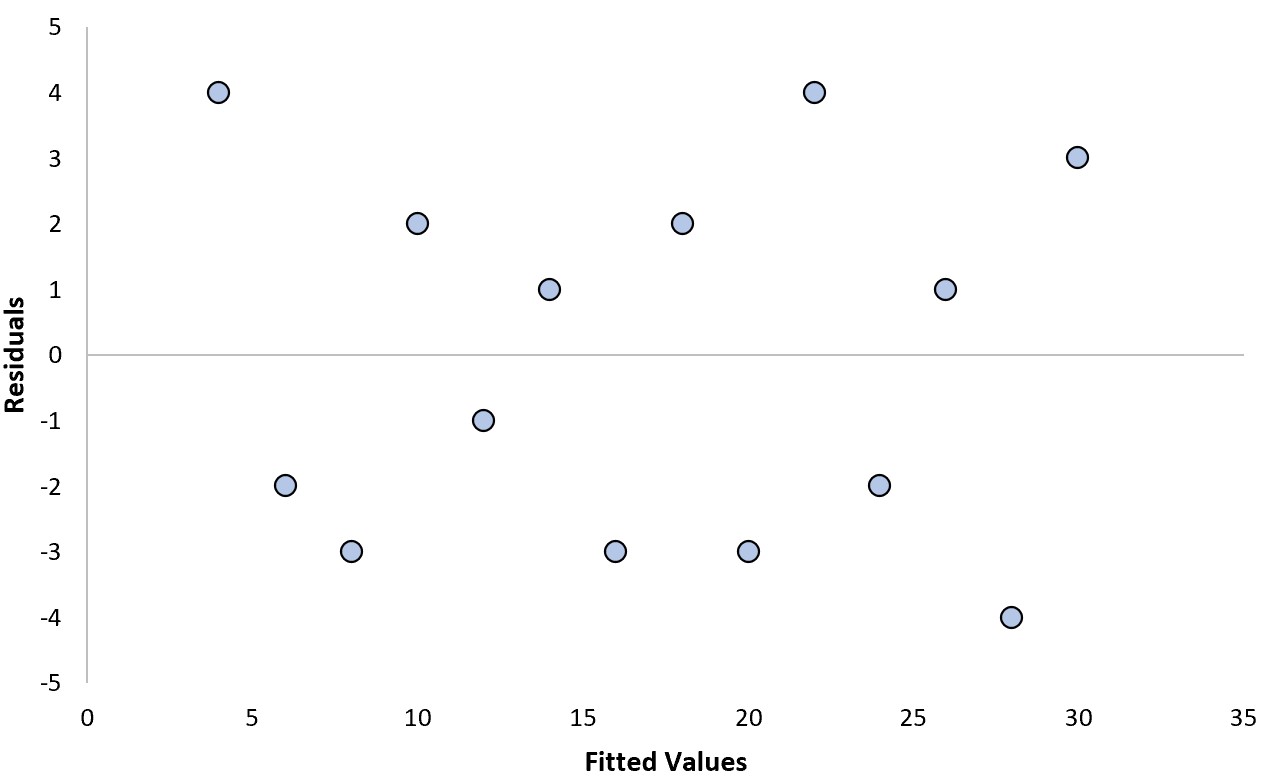
Мы можем ответить на следующие два вопроса, чтобы определить, является ли это «хорошим» остаточным графиком:

1. Показывают ли остатки четкую тенденцию?

Нет. Остатки случайным образом разбросаны вокруг нуля и не имеют четкой закономерности.

2. Систематически ли увеличиваются или уменьшаются дисперсии остатков?

Нет. Остатки имеют довольно постоянную дисперсию (т. е. расстояние между остатками и нулевым значением) на каждом уровне подобранных значений.

Поскольку мы ответили «Нет» на оба этих вопроса, мы бы сочли это «хорошим» остаточным графиком.

Следовательно, мы можем доверять результатам регрессионной модели и безопасно интерпретировать коэффициенты модели.

Пример 2: «плохой» остаточный график с четкой моделью

Предположим, мы подбираем регрессионную модель и получаем следующий остаточный график:

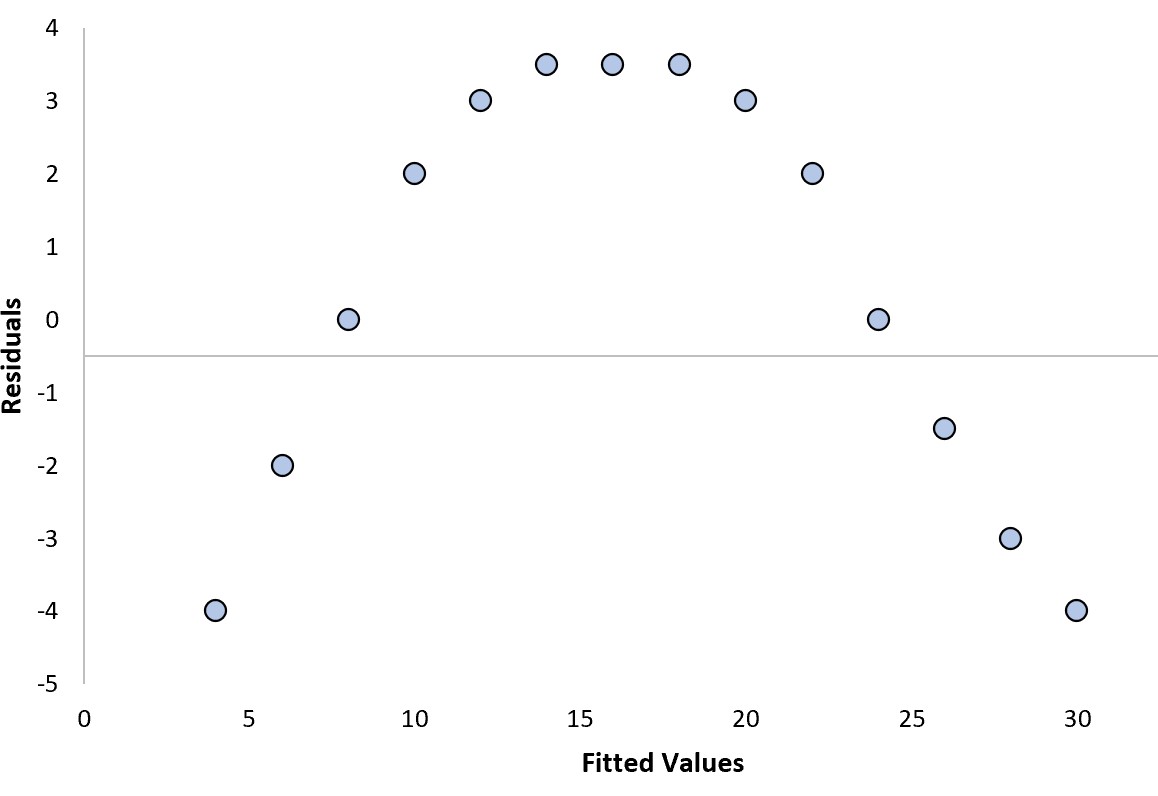
Мы можем ответить на следующие два вопроса, чтобы определить, является ли это «хорошим» остаточным графиком:

1. Показывают ли остатки четкую тенденцию?

Да . Остатки имеют изогнутую форму.

2. Систематически ли увеличиваются или уменьшаются дисперсии остатков?

Да . Остатки имеют разные уровни дисперсии на разных уровнях подобранных значений.

Поскольку мы ответили «Да» хотя бы на один из этих вопросов, мы бы сочли это «плохим» остаточным сюжетом.

Это означает, что регрессионная модель не обеспечивает хорошего соответствия данным.

В частности, изогнутый рисунок на графике остатков указывает на то, что модель линейной регрессии не соответствует данным и что модель квадратической регрессии, вероятно, справится с этой задачей лучше.

Пример 3: «плохой» график остатков с возрастающей дисперсией

Предположим, мы подбираем регрессионную модель и получаем следующий остаточный график:

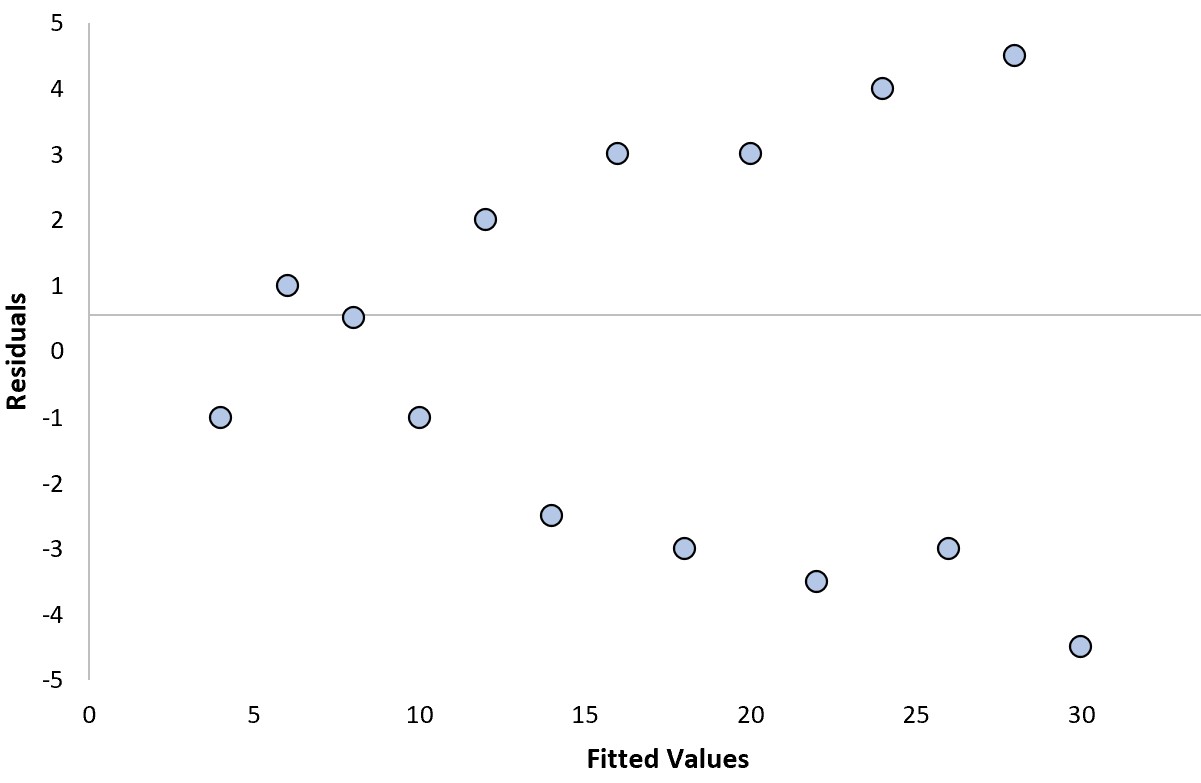
Мы можем ответить на следующие два вопроса, чтобы определить, является ли это «хорошим» остаточным графиком:

1. Показывают ли остатки четкую тенденцию?

Нет. Четкой тенденции в остатках нет.

2. Систематически ли увеличиваются или уменьшаются дисперсии остатков?

Да . Дисперсия остатков увеличивается по мере увеличения подобранных значений.

Поскольку мы ответили «Да» хотя бы на один из этих вопросов, мы бы сочли это «плохим» остаточным сюжетом.

В этом конкретном примере остатки страдают от гетероскедастичности , которая относится к неравной дисперсии остатков на разных уровнях подобранных значений.

Это означает, что результаты регрессионной модели могут быть ненадежными.

Обратитесь к этой статье , чтобы узнать о различных способах решения проблемы гетероскедастичности в регрессионной модели.

Дополнительные ресурсы

В следующих руководствах объясняется, как создавать графики остатков с использованием различного статистического программного обеспечения:

Как создать остаточный график в R
Как создать остаточный график в Python
Как создать остаточный график в Excel
Как создать остаточный график в SAS