Как применить центральную предельную теорему в excel

Центральная предельная теорема утверждает, что выборочное распределение выборочного среднего примерно нормально, если размер выборки достаточно велик, даже если распределение совокупности не является нормальным .

Центральная предельная теорема также утверждает, что выборочное распределение будет иметь следующие свойства:

1. Среднее значение выборочного распределения будет равно среднему значению распределения совокупности:

х = µ

2. Стандартное отклонение выборочного распределения будет равно стандартному отклонению генеральной совокупности, деленному на размер выборки:

s = σ / √n

В этом уроке мы объясним, как применить центральную предельную теорему в Excel к заданному распределению.

Применение центральной предельной теоремы в Excel

Предположим, у нас есть распределение со средним значением 8 и стандартным отклонением 4 . Мы можем использовать следующие формулы в Excel, чтобы найти среднее и стандартное отклонение распределения выборки с размером выборки 15 :

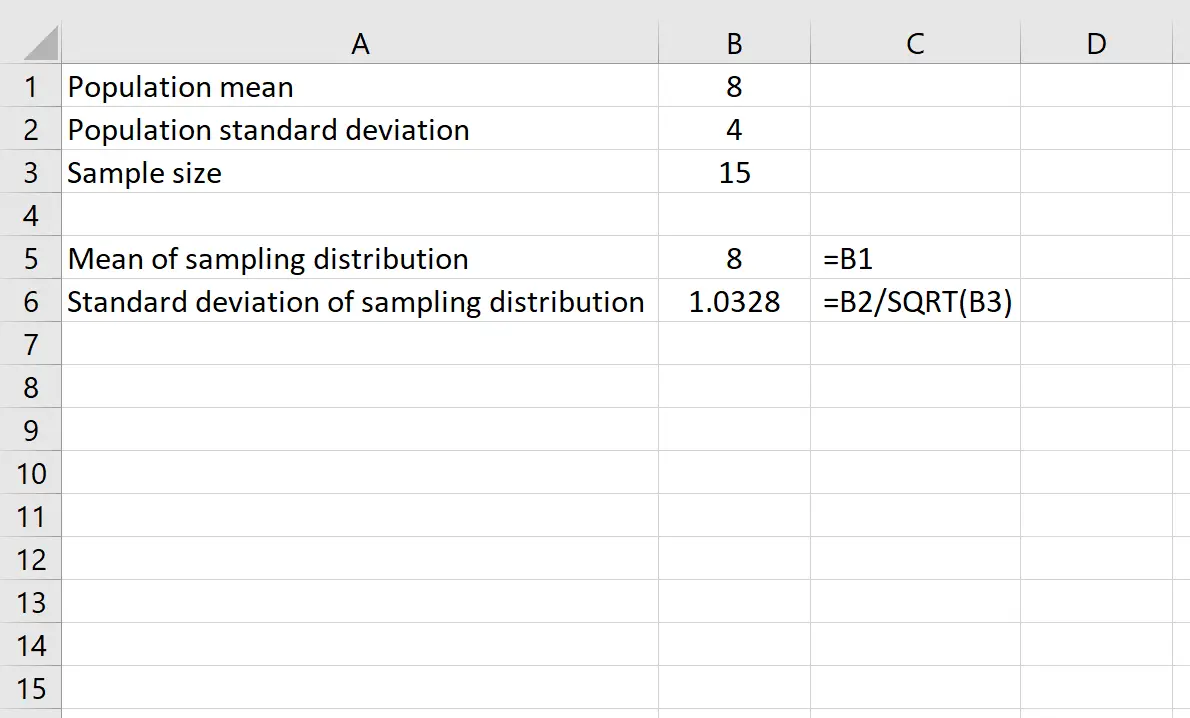
Среднее значение распределения выборки просто равно среднему значению распределения населения, которое равно 8 .

Стандартное отклонение выборочного распределения равно стандартному отклонению генеральной совокупности, деленному на размер выборки, или: 4 /√15 = 1,0328 .

Мы также можем использовать центральную предельную теорему, чтобы ответить на вопросы о вероятности. Например, если данная совокупность имеет среднее значение 8 и стандартное отклонение 4 , какова вероятность того, что данная выборка размером 15   имеет среднее значение меньше или равно 7 ?

Чтобы ответить на этот вопрос, мы можем использовать функцию НОРМ.РАСП() в Excel, которая использует следующий синтаксис:

НОРМ.РАСП(x, среднее, стандартное_отклонение, совокупное)

Золото:

• x: образец означает, что вы хотите протестировать
• среднее: ожидаемое среднее выборочного распределения
• Standard_dev: ожидаемое стандартное отклонение выборочного распределения.
• накопительный: TRUE возвращает нормальное значение CDF; FALSE возвращает значение обычного PDF. В нашем случае мы всегда будем использовать TRUE.

Эта функция вернет вероятность того, что выборочное среднее меньше или равно определенному значению.

Вот формула, которую мы будем использовать в этом примере:

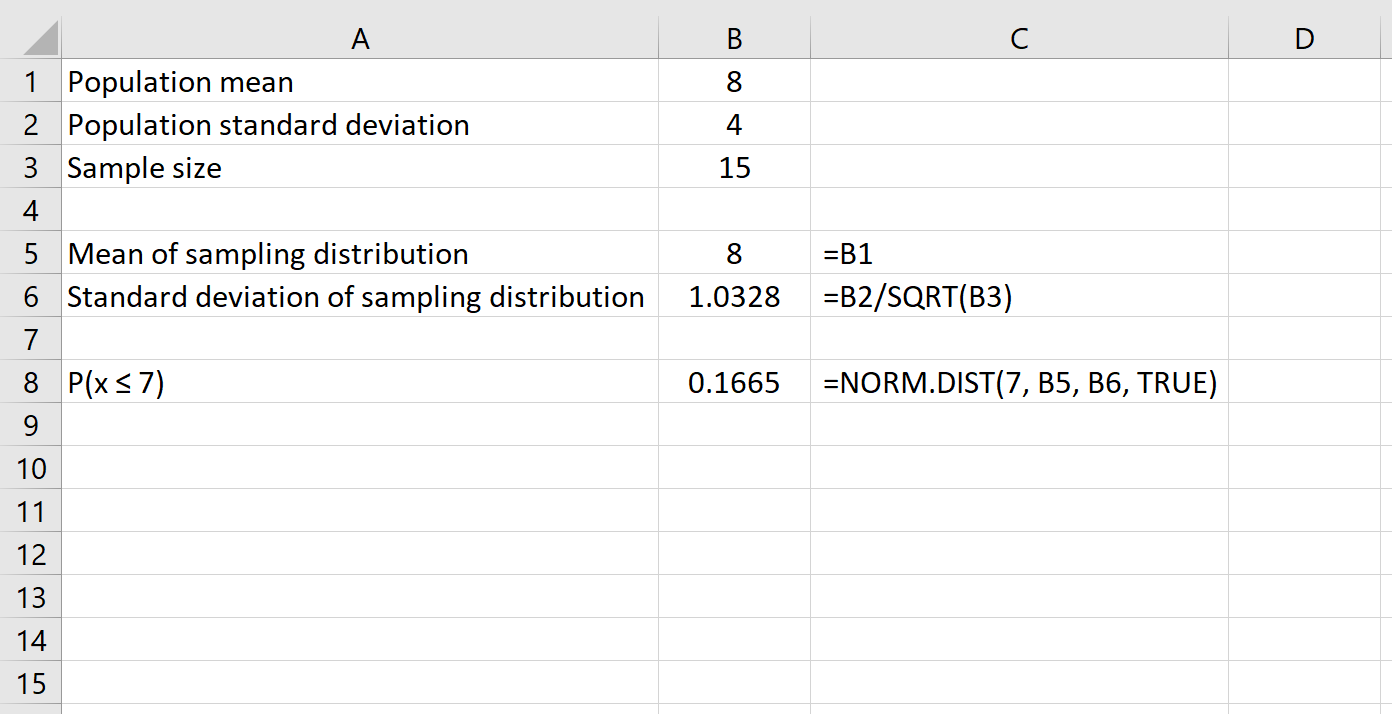
Это говорит нам о том, что для совокупности со средним значением 8 и стандартным отклонением 4 вероятность того, что данная выборка размером 15   имеет среднее значение меньше или равное 7 или 0,1665 .

Мы также можем найти вероятность того, что данный размер выборки будет иметь среднее значение, превышающее определенное число, просто используя формулу 1 — NORM.DIST() .

Например, следующая формула показывает, как определить вероятность того, что при данном размере выборки, равном 15, среднее значение будет больше 7:

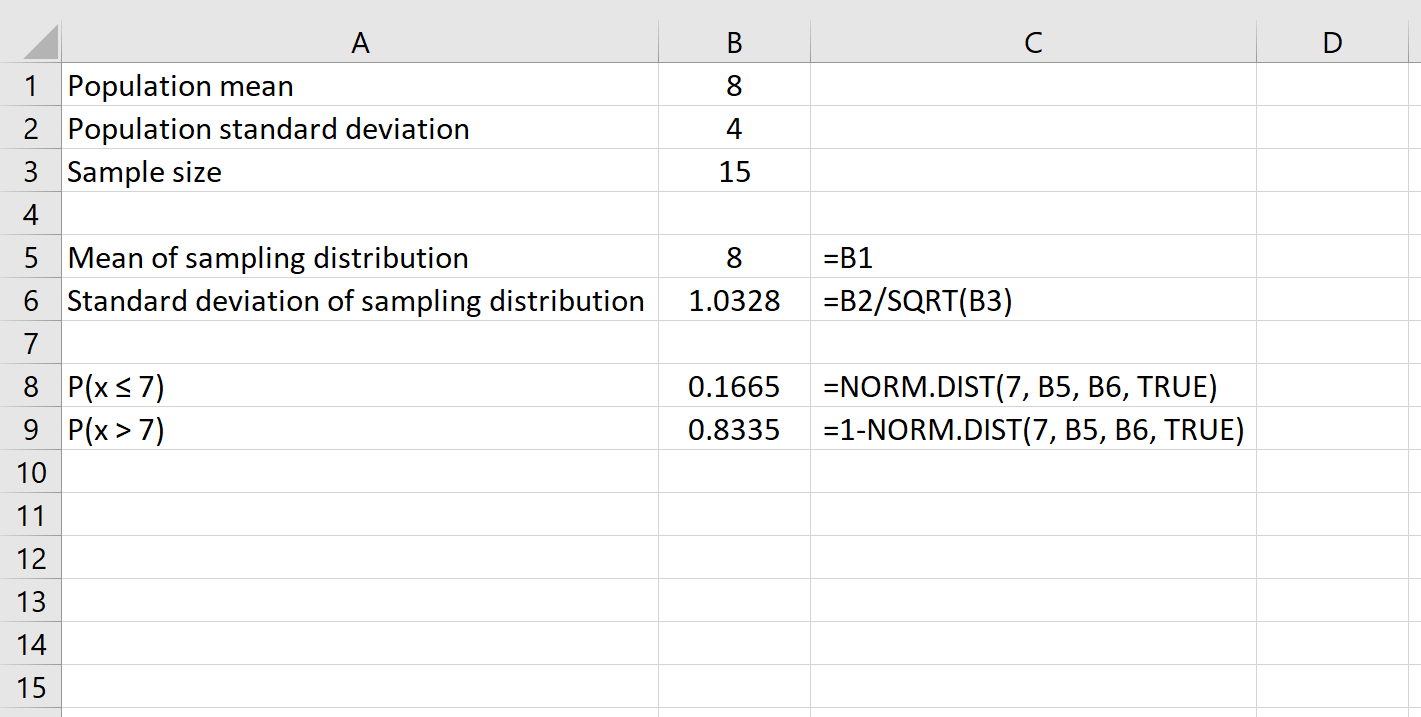
Наконец, мы можем найти вероятность того, что данный размер выборки имеет среднее между двумя числами, используя формулу НОРМ.РАСП(большее число) – НОРМ.РАСП(меньшее число) .

Например, следующая формула показывает, как найти вероятность того, что заданный размер выборки, равный 15, имеет среднее значение от 7 до 9:

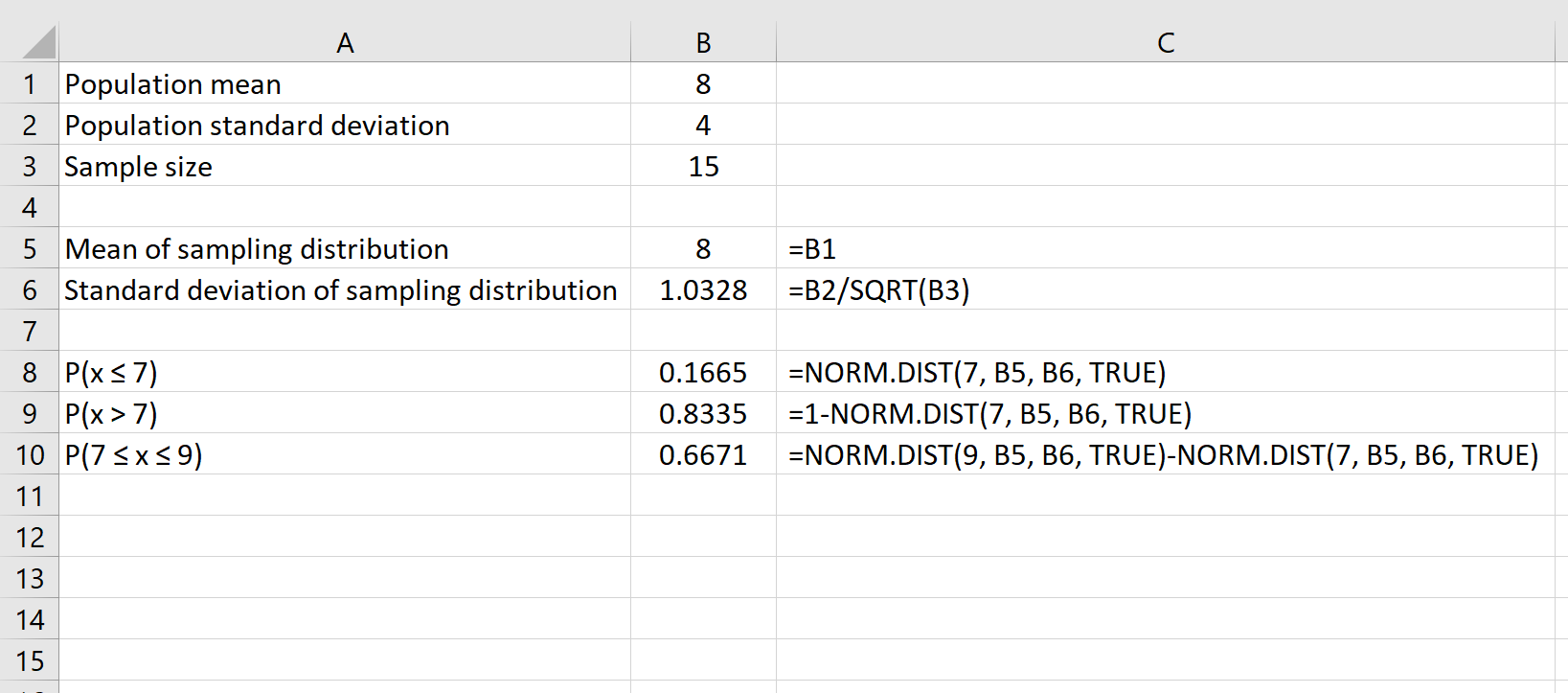
Дополнительные ресурсы

Калькулятор центральной предельной теоремы
Как применить эмпирическое правило в Excel
Как создать колоколообразную кривую в Excel