Как применить центральную предельную теорему к калькулятору ti-84

Центральная предельная теорема утверждает, что выборочное распределение выборочного среднего примерно нормально, если размер выборки достаточно велик, даже если распределение совокупности не является нормальным.

Центральная предельная теорема также утверждает, что выборочное распределение будет иметь следующие свойства:

1. Среднее значение выборочного распределения будет равно среднему значению распределения совокупности:

х = µ

2. Стандартное отклонение выборочного распределения будет равно стандартному отклонению генеральной совокупности, деленному на размер выборки:

s = σ / √n

Чтобы найти вероятности, связанные с выборочным средним значением, на калькуляторе TI-84, мы можем использовать функциюnormalcdf () со следующим синтаксисом:

 normalcdf (lower value, upper value, x , s/√ n )

Золото:

• x : выборочное среднее
• s : выборочное стандартное отклонение
• n : размер выборки

Чтобы получить доступ к этой функции на калькуляторе TI-84, просто нажмите 2nd , затем нажмите VARS , затем перейдите к файлуnormalcdf ( и нажмите ENTER) .

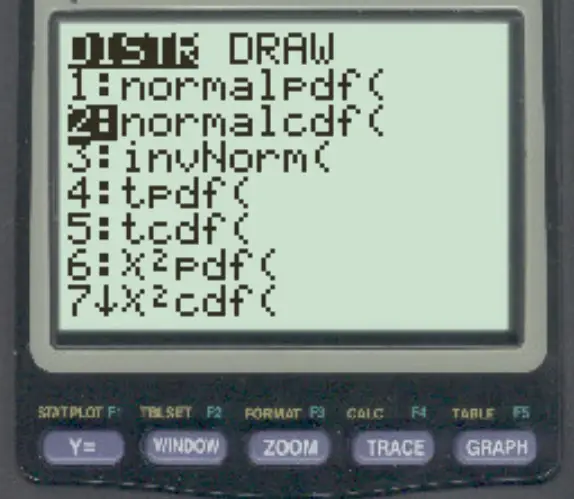
Следующие примеры показывают, как использовать эту функцию на практике.

Пример 1. Найдите вероятность между двумя значениями.

Распределение имеет среднее значение 70 и стандартное отклонение 7. Если мы выберем случайную выборку размером n = 35, найдите вероятность того, что среднее значение выборки находится между 68 и 72.

Мы можем использовать следующий синтаксис на TI-84:

 normalcdf (68, 72, 70, 7/√ 35 ) 

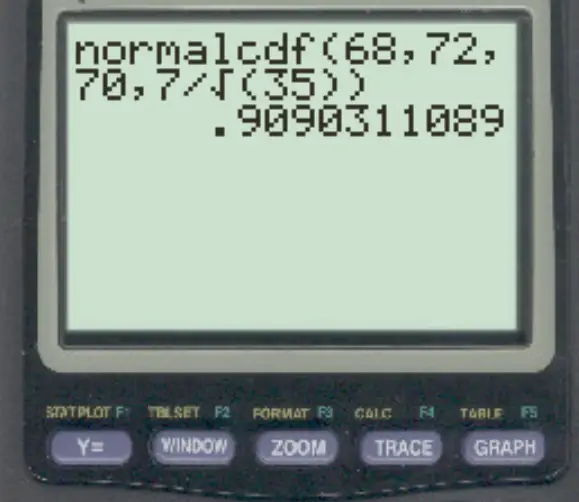
Вероятность того, что выборочное среднее находится между 68 и 72, равна 0,909 .

Пример 2: Нахождение вероятности, большей значения

Распределение имеет среднее значение 50 и стандартное отклонение 4. Если мы выберем случайную выборку размером n = 30, найдите вероятность того, что среднее значение выборки больше 48.

Мы можем использовать следующий синтаксис на TI-84:

 normalcdf (48, E99, 50, 4/√ 30 )

Примечание. Вы можете получить доступ к символу «E», нажав 2 , а затем кнопку , .

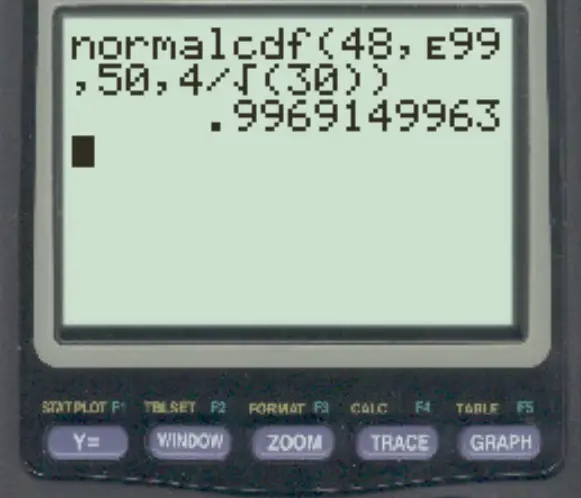
Вероятность того, что выборочное среднее больше 48, равна 0,9969 .

Пример 3: Нахождение вероятности меньше значения

Распределение имеет среднее значение 20 и стандартное отклонение 3. Если мы выберем случайную выборку размером n = 40, найдите вероятность того, что среднее значение выборки будет меньше 19.

Мы можем использовать следующий синтаксис на TI-84:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

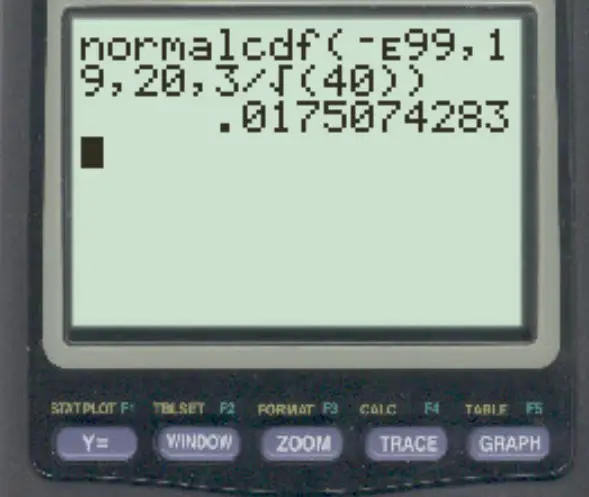
Вероятность того, что выборочное среднее меньше 19, равна 0,0175 .

Дополнительные ресурсы

Введение в центральную предельную теорему
Калькулятор центральной предельной теоремы
Как применить центральную предельную теорему в Excel
Центральная предельная теорема: четыре условия, которые необходимо выполнить