Как применить центральную предельную теорему в r (с примерами)

Центральная предельная теорема утверждает, что выборочное распределение выборочного среднего примерно нормально, если размер выборки достаточно велик, даже если распределение совокупности не является нормальным.

Центральная предельная теорема также утверждает, что выборочное распределение будет иметь следующие свойства:

1. Среднее значение выборочного распределения будет равно среднему значению распределения совокупности:

х = µ

2. Стандартное отклонение выборочного распределения будет равно стандартному отклонению распределения совокупности, деленному на размер выборки:

s = σ /n

Следующий пример показывает, как применить центральную предельную теорему в R.

Пример: применение центральной предельной теоремы в R

Предположим, что ширина панциря черепахи равномерно распределена : минимальная ширина 2 дюйма и максимальная ширина 6 дюймов.

То есть, если мы наугад выберем черепаху и измерим ширину ее панциря, она, скорее всего, также будет от 2 до 6 дюймов в ширину .

Следующий код показывает, как создать набор данных в R, содержащий измерения ширины панциря 1000 черепах, равномерно распределенных между 2 и 6 дюймами:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

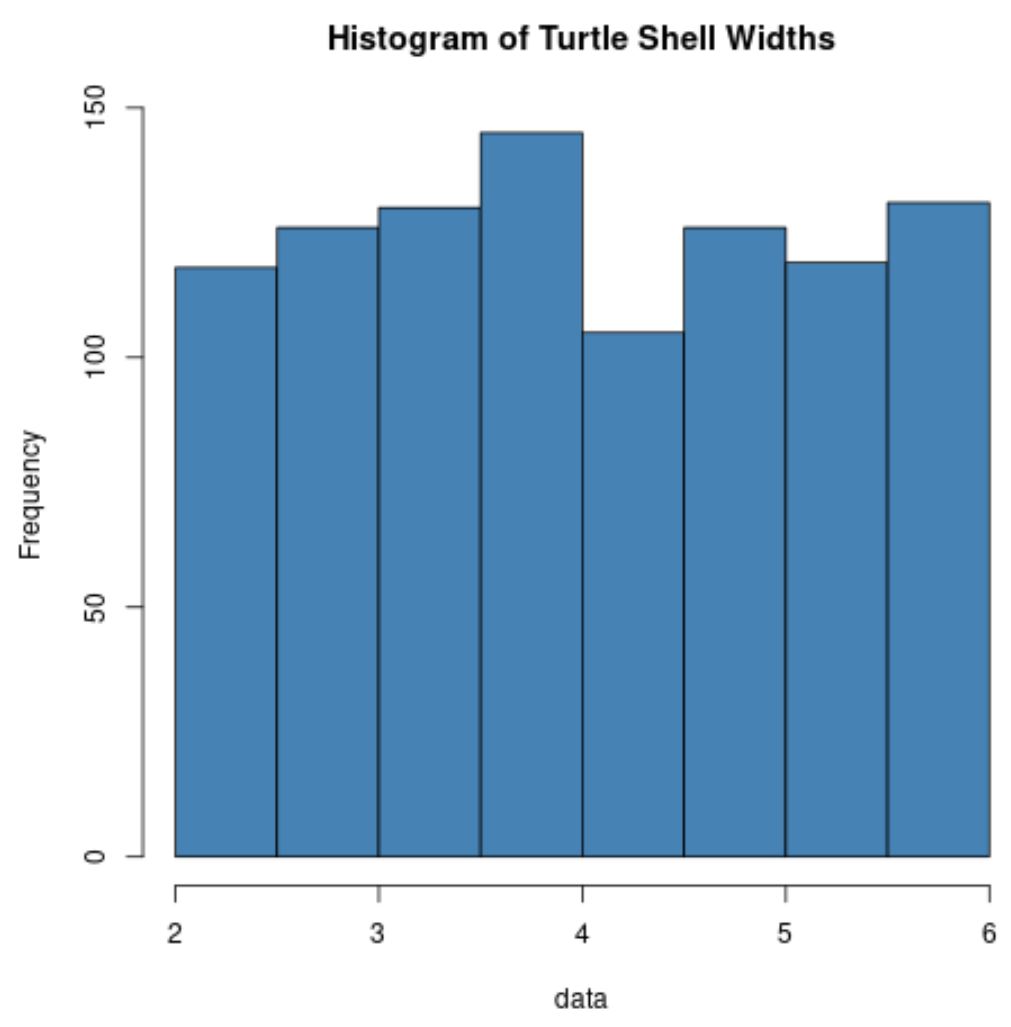
Обратите внимание, что распределение ширины панциря черепахи обычно не распределено вообще.

Теперь представьте, что мы берем повторяющиеся случайные выборки из 5 черепах из этой популяции и снова и снова измеряем среднее значение выборки.

Следующий код показывает, как выполнить этот процесс в R и создать гистограмму для визуализации распределения выборочных средних:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

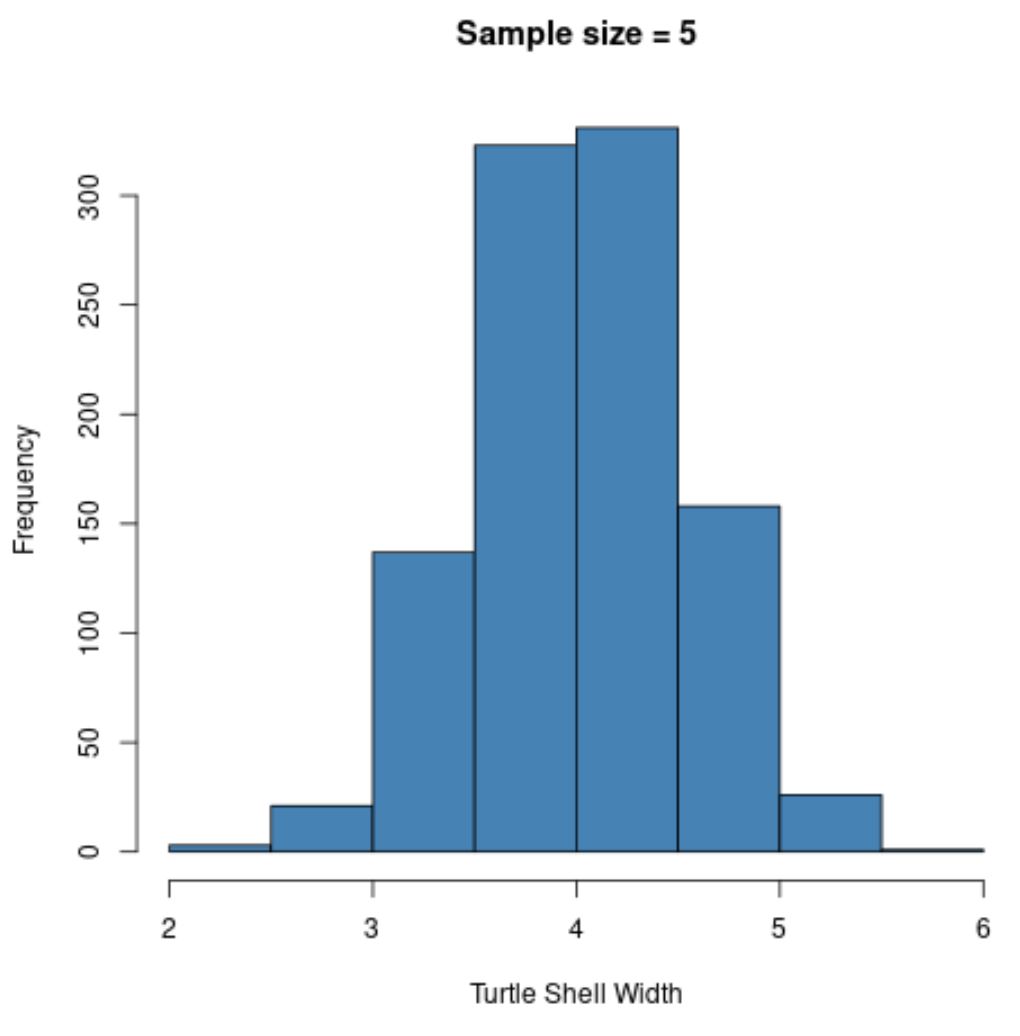
Обратите внимание, что распределение выборочных средних выглядит нормально распределенным, хотя распределение, из которого взяты выборки, не было нормально распределенным.

Также обратите внимание на выборочное среднее и выборочное стандартное отклонение для этого выборочного распределения:

• х̄ : 4,008
• с : 0,517

Теперь предположим, что мы увеличиваем размер используемой выборки с n=5 до n=30 и воссоздаем гистограмму выборочных средних:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

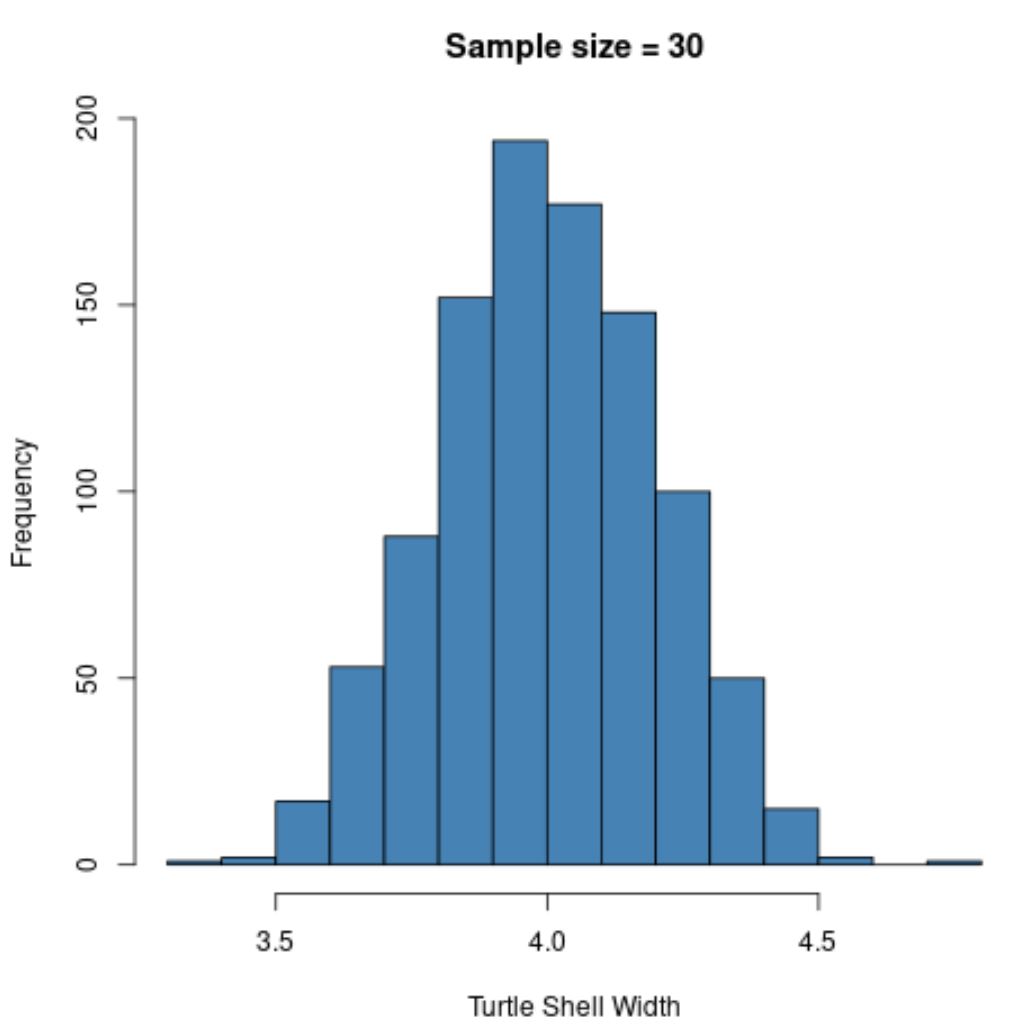
Распределение выборки снова имеет нормальное распределение , но стандартное отклонение выборки еще меньше:

• с : 0,200

Это связано с тем, что мы использовали больший размер выборки (n=30) по сравнению с предыдущим примером (n=5), поэтому стандартное отклонение выборочных средних еще меньше.

Если мы продолжим использовать все большие и большие выборки, мы обнаружим, что стандартное отклонение выборки становится все меньше и меньше.

Это иллюстрирует центральную предельную теорему на практике.

Дополнительные ресурсы

Следующие ресурсы предоставляют дополнительную информацию о центральной предельной теореме:

Введение в центральную предельную теорему
Калькулятор центральной предельной теоремы
5 примеров использования центральной предельной теоремы в реальной жизни