Что означает высокое значение f в anova?
Однофакторный дисперсионный анализ используется для определения того, равны ли средние значения трех или более независимых групп.
Односторонний дисперсионный анализ использует следующие нулевые и альтернативные гипотезы:
- H 0 : Все средние значения группы равны.
- Х А : По крайней мере, одно среднее значение группы отличается от других.
Каждый раз, когда вы выполняете однофакторный дисперсионный анализ, вы получаете сводную таблицу, которая выглядит следующим образом:
| Источник | Сумма квадратов (СС) | дф | Среднеквадратичные (МС) | Ф | P-значение |
|---|---|---|---|---|---|
| Уход | 192,2 | 2 | 96,1 | 2358 | 0,1138 |
| Ошибка | 1100,6 | 27 | 40,8 | ||
| Общий | 1292,8 | 29 |
Значение F в таблице рассчитывается следующим образом:
- Значение F = обработка среднеквадратических значений / ошибка среднеквадратических значений
Другой способ написать это:
- F-значение = вариация между средними значениями выборки / вариация внутри выборки
Если разница между средними значениями выборки велика по сравнению с вариацией внутри каждой выборки, то значение F будет большим.
Например, значение F в таблице выше рассчитывается следующим образом:
- Значение F = 96,1 / 40,8 = 2,358
Чтобы найти значение p , соответствующее этому значению F, мы можем использовать калькулятор F-распределения со степенями свободы в числителе = df Лечение и степенями свободы в знаменателе = df Ошибка.
Например, значение p, соответствующее значению F 2,358, числителю df = 2 и знаменателю df = 27, равно 0,1138 .
Поскольку это значение p не меньше α = 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что нет статистически значимой разницы между средними значениями трех групп.
Просмотр значения F дисперсионного анализа
Чтобы получить интуитивное представление о значении F в таблице ANOVA, рассмотрим следующий пример.
Предположим, мы хотим выполнить однофакторный дисперсионный анализ, чтобы определить, дают ли три разных метода обучения разные средние баллы на экзамене. В следующей таблице показаны результаты экзамена 10 студентов, использовавших каждый метод:
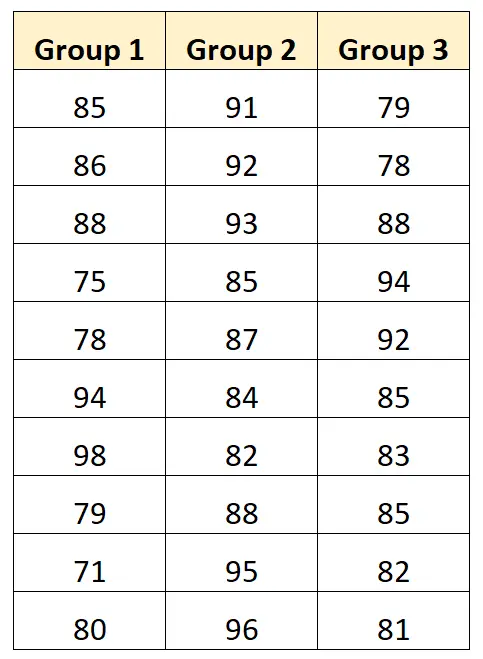
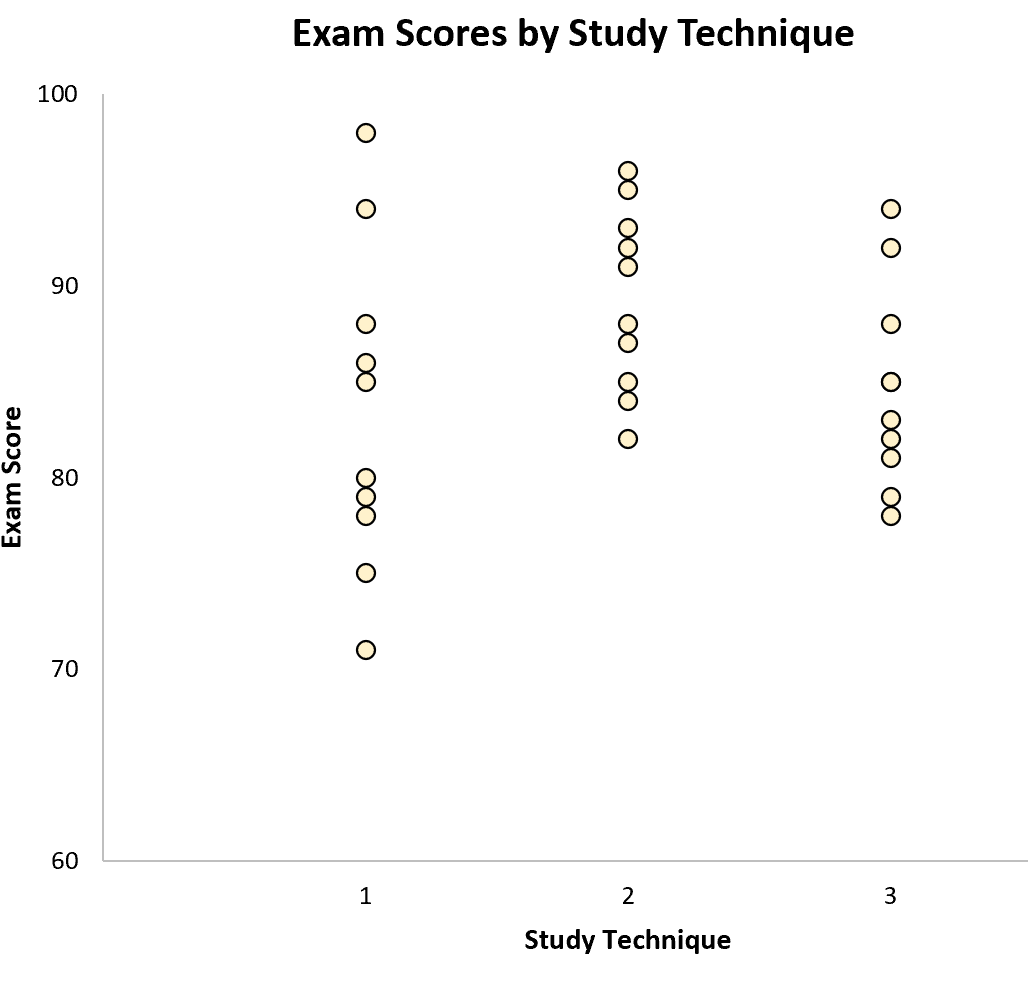
Мы можем создать следующую диаграмму для визуализации результатов экзамена по группам:
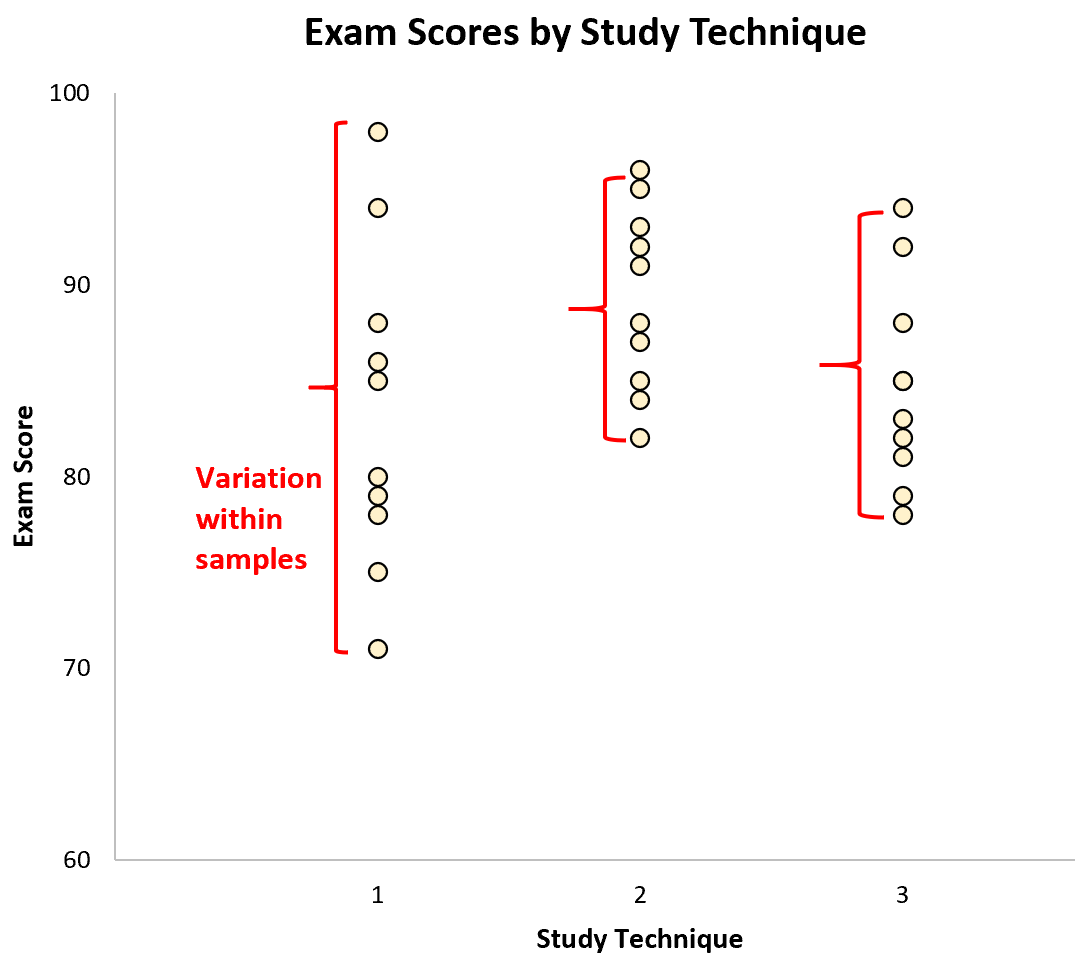
Вариация внутри выборок представлена распределением значений внутри каждой отдельной выборки:
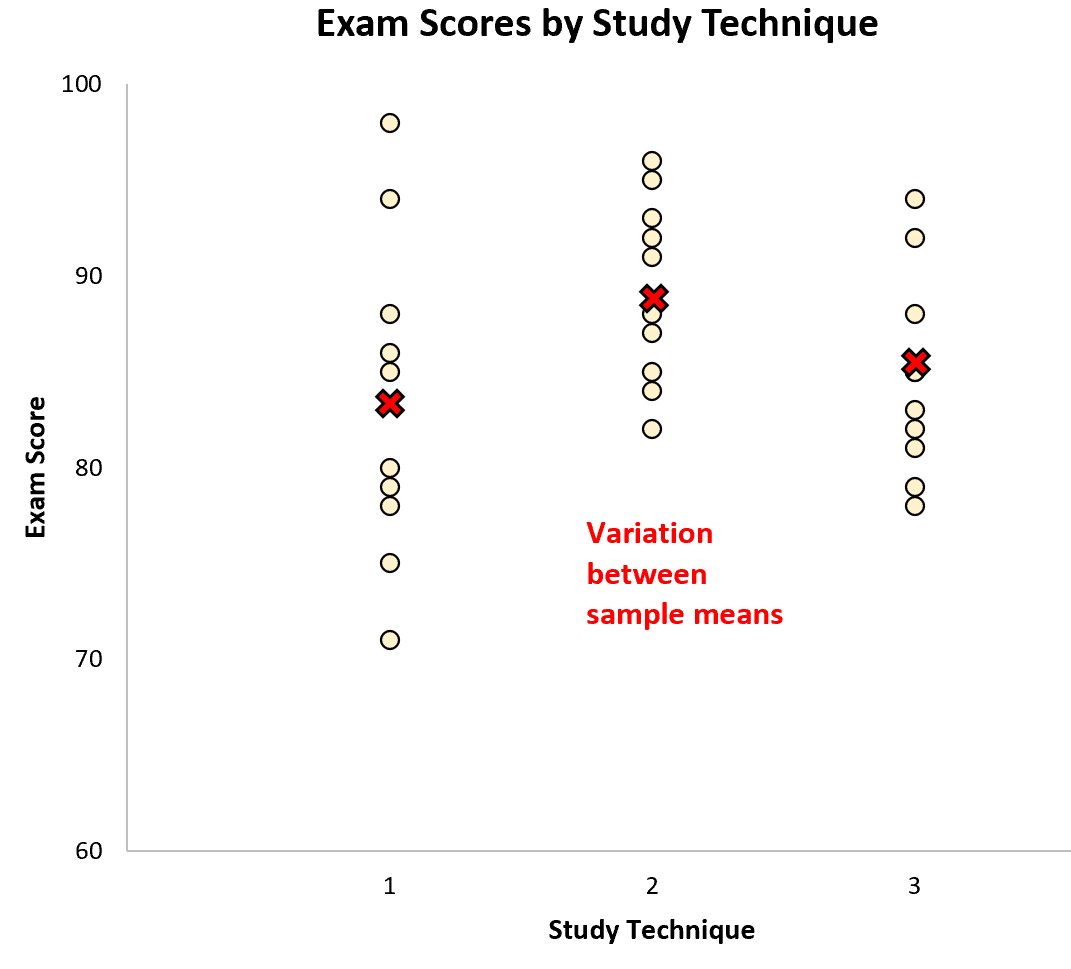
Вариации между выборками представлены различиями между выборочными средними:
Выполняя однофакторный дисперсионный анализ для этого набора данных, мы обнаруживаем, что значение F составляет 2,358 , а соответствующее значение p — 0,1138 .
Поскольку это значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас недостаточно доказательств, чтобы утверждать, что использованная методика исследования приводит к статистически значимым различиям в средних баллах на экзамене.
Другими словами, это говорит нам о том, что вариация между выборочными средними недостаточно велика по сравнению с вариацией внутри выборки, чтобы отвергнуть нулевую гипотезу.
Заключение
Вот краткое изложение основных положений этой статьи:
- Значение F в ANOVA рассчитывается как: вариация между средними выборками / вариация внутри выборки.
- Чем выше значение F в дисперсионном анализе, тем больше разница между средними выборками по сравнению с вариациями внутри выборок.
- Чем выше значение F, тем ниже соответствующее значение p.
- Если значение p ниже определенного порога (например, α = 0,05), мы можем отклонить нулевую гипотезу ANOVA и сделать вывод, что существует статистически значимая разница между групповыми средними значениями.
Дополнительные ресурсы
Как выполнить однофакторный дисперсионный анализ в Excel
Как вручную выполнить однофакторный дисперсионный анализ
Односторонний калькулятор ANOVA