Что считается «слабым»; корреляция?
В статистике мы часто стремимся понять, как две переменные связаны друг с другом. Например, нам может быть интересно узнать:
- Какова связь между количеством часов обучения студента и оценкой, которую он получает на экзамене?
- Какова связь между температурой наружного воздуха и количеством батончиков мороженого, проданных фургоном с едой?
- Какова связь между долларами, потраченными на рекламу, и общим доходом, полученным от данного бизнеса?
В каждом сценарии мы хотим понять взаимосвязь между двумя переменными.
Одним из наиболее распространенных способов количественной оценки связи между двумя переменными является использование коэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными.
Он всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Это число, часто обозначаемое r , помогает нам понять силу связи между двумя переменными. Чем ближе r к нулю, тем слабее связь между двумя переменными .
Важно отметить, что две переменные могут иметь слабую положительную корреляцию или слабую отрицательную корреляцию.
Слабая положительная корреляция: когда одна переменная увеличивается, другая переменная также имеет тенденцию к увеличению, но лишь слабо или ненадежно.
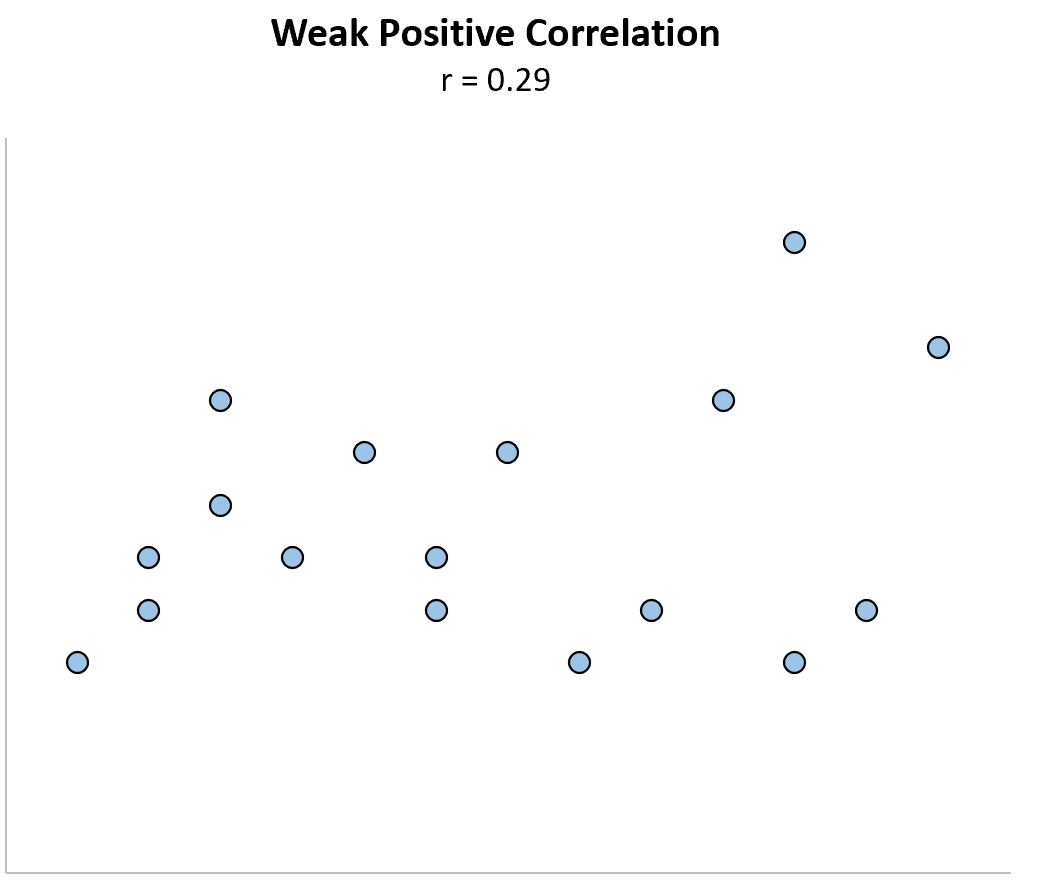
Низкая отрицательная корреляция: когда одна переменная увеличивается, другая имеет тенденцию к уменьшению, но лишь слабо или ненадежно.
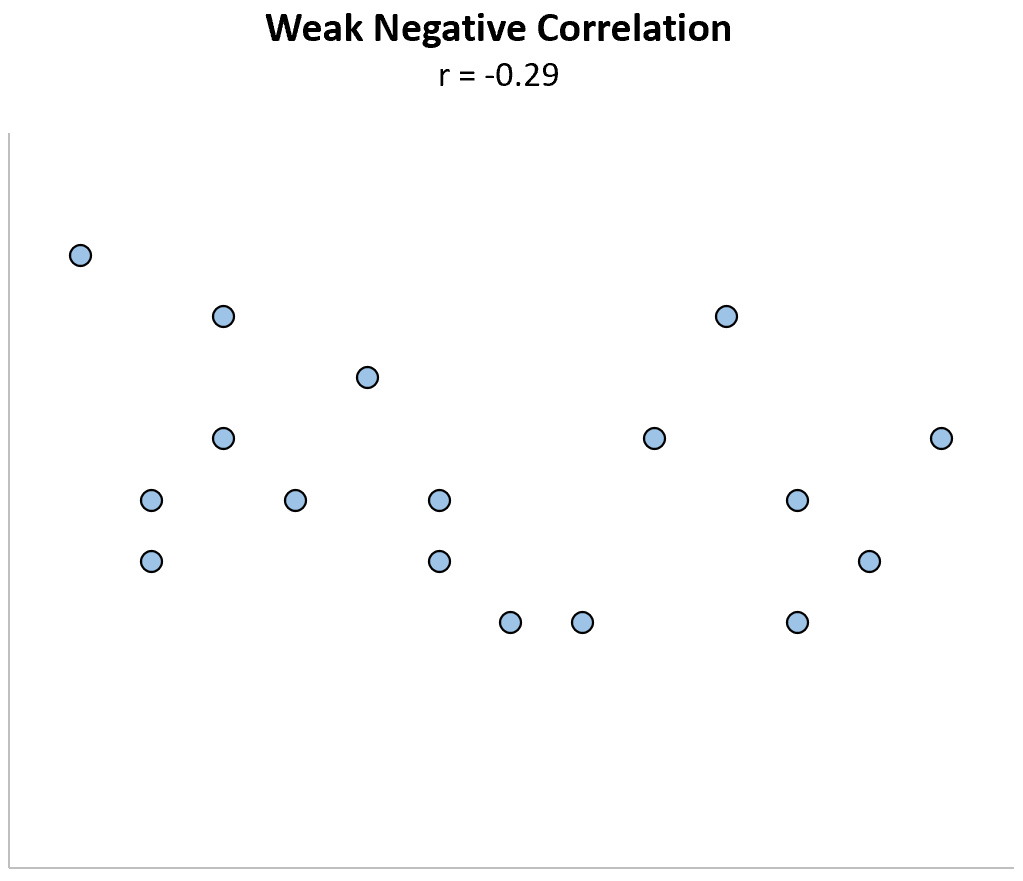
В следующей таблице показано практическое правило интерпретации силы связи между двумя переменными на основе значения r :
| Абсолютное значение r | Сила отношений |
|---|---|
| р < 0,25 | Нет отношений |
| 0,25 < г < 0,5 | Слабые отношения |
| 0,5 < г < 0,75 | Умеренные отношения |
| г > 0,75 | Прочные отношения |
Корреляция между двумя переменными считается низкой, если абсолютное значение r находится между 0,25 и 0,5.
Однако определение «слабой» корреляции может варьироваться от поля к полю.
Медицинский
В медицинских областях определение «слабых» отношений часто гораздо ниже. Если связь между приемом определенного препарата и уменьшением количества сердечных приступов равна r = 0,2, в других областях это можно было бы считать «отсутствием связи», но в медицине это достаточно значимо, поэтому стоит принимать лекарство, чтобы снизить риск сердечных приступов. . случиться сердечный приступ.
Человеческие ресурсы
В такой области, как человеческие ресурсы, более низкие корреляции также используются чаще. Например, было показано, что корреляция между средним баллом в колледже и производительностью труда составляет примерно r = 0,16 . Это довольно низкая цифра, но она достаточно важна, чтобы компания, по крайней мере, учитывала это во время собеседования.
Технологии
В технологических областях корреляция между переменными, возможно, должна быть намного выше, чтобы считаться «низкой». Например, если компания создает беспилотный автомобиль и корреляция между решениями автомобиля о повороте и вероятностью избежать аварии равна r = 0,95 , это можно считать «слабой» корреляцией и, вероятно, слишком слабой для того, чтобы автомобиль мог считаться безопасным, поскольку неправильное решение может оказаться фатальным.
Используйте диаграммы рассеяния для визуализации корреляций
При расчете коэффициента корреляции между двумя переменными полезно также создать диаграмму рассеяния, чтобы визуализировать корреляцию.
В частности, облака точек имеют два преимущества:
1. Диаграммы рассеяния могут помочь вам выявить выбросы, влияющие на коэффициент корреляции.
Экстремальный выброс может оказать большое влияние на коэффициент корреляции. Рассмотрим пример ниже, в котором переменные X и Y имеют коэффициент корреляции Пирсона r = 0,91 .
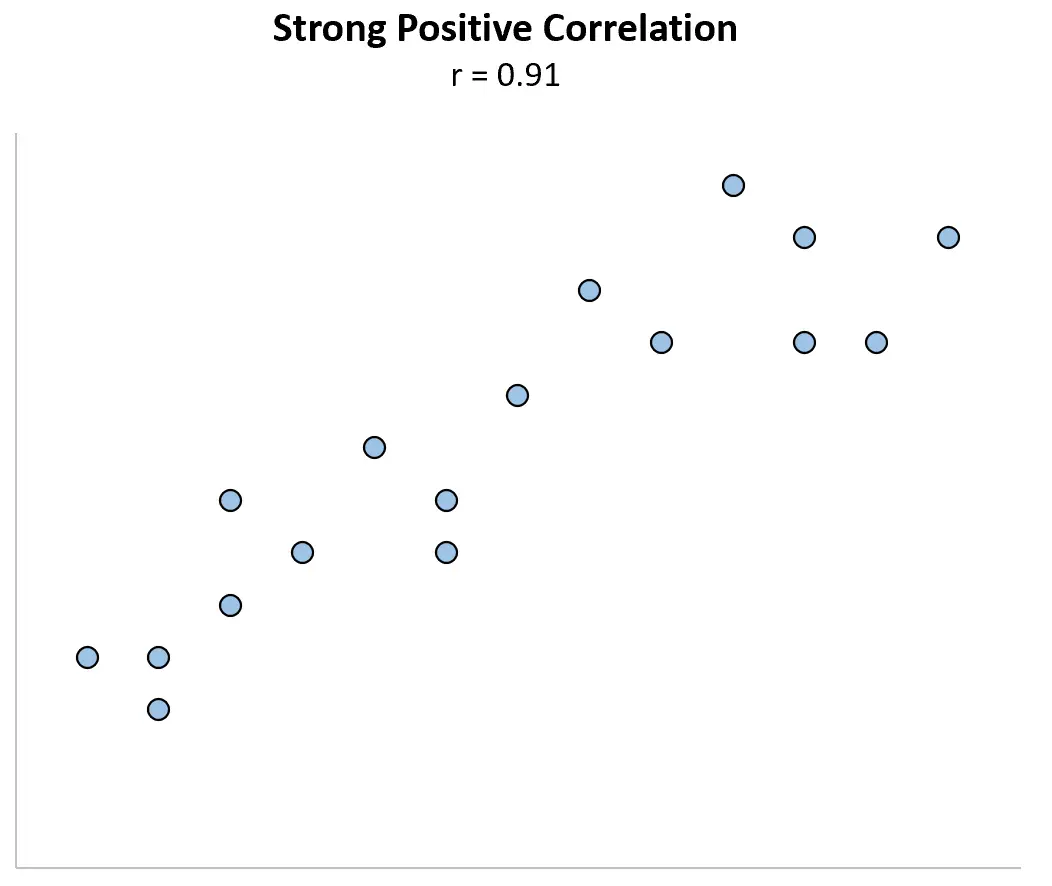
Теперь представьте, что мы изменяем первую точку данных, чтобы она стала намного больше. Коэффициент корреляции внезапно становится r = 0,29 .
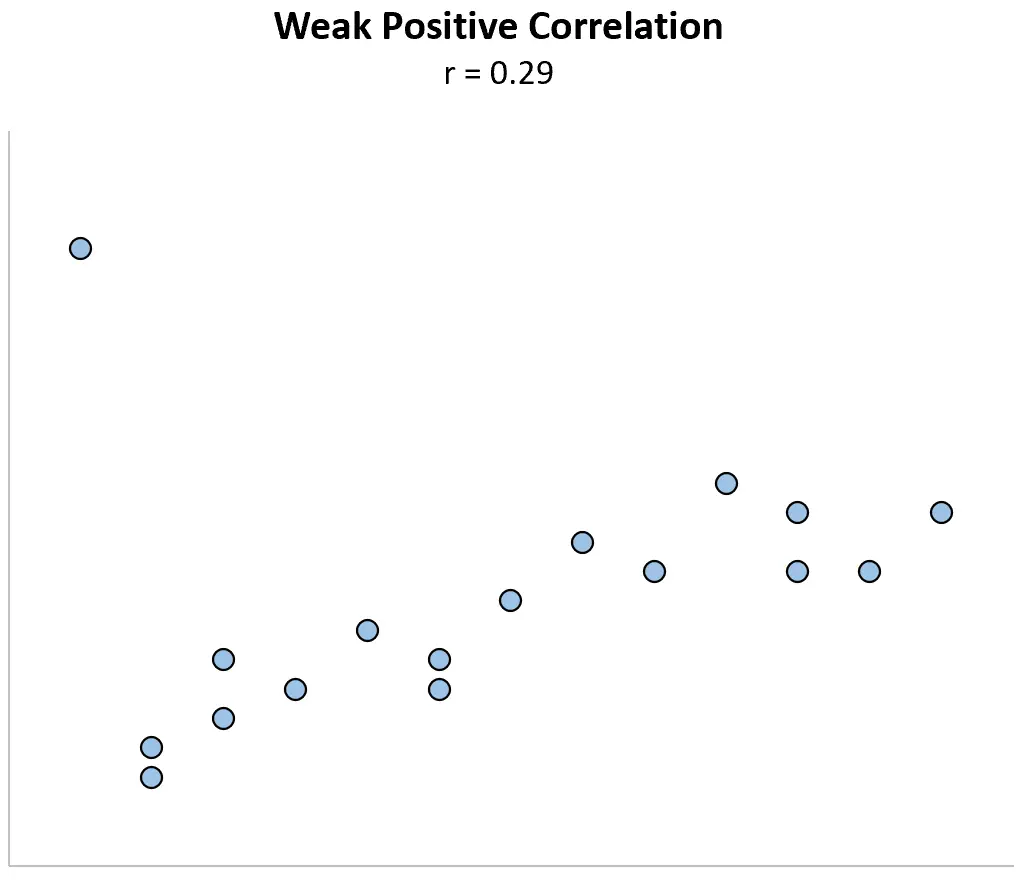
Эта единственная точка данных меняет коэффициент корреляции с сильно положительной связи на слабо положительную связь.
(2) Диаграммы рассеяния могут помочь вам выявить нелинейные связи между переменными.
Коэффициент корреляции Пирсона просто говорит нам, связаны ли две переменные линейно . Но даже если коэффициент корреляции Пирсона говорит нам, что две переменные не коррелируют, между ними все равно может быть какая-то нелинейная связь.
Например, рассмотрим приведенную ниже диаграмму рассеяния между переменными X и Y , в которой их корреляция равна r = 0,00 .
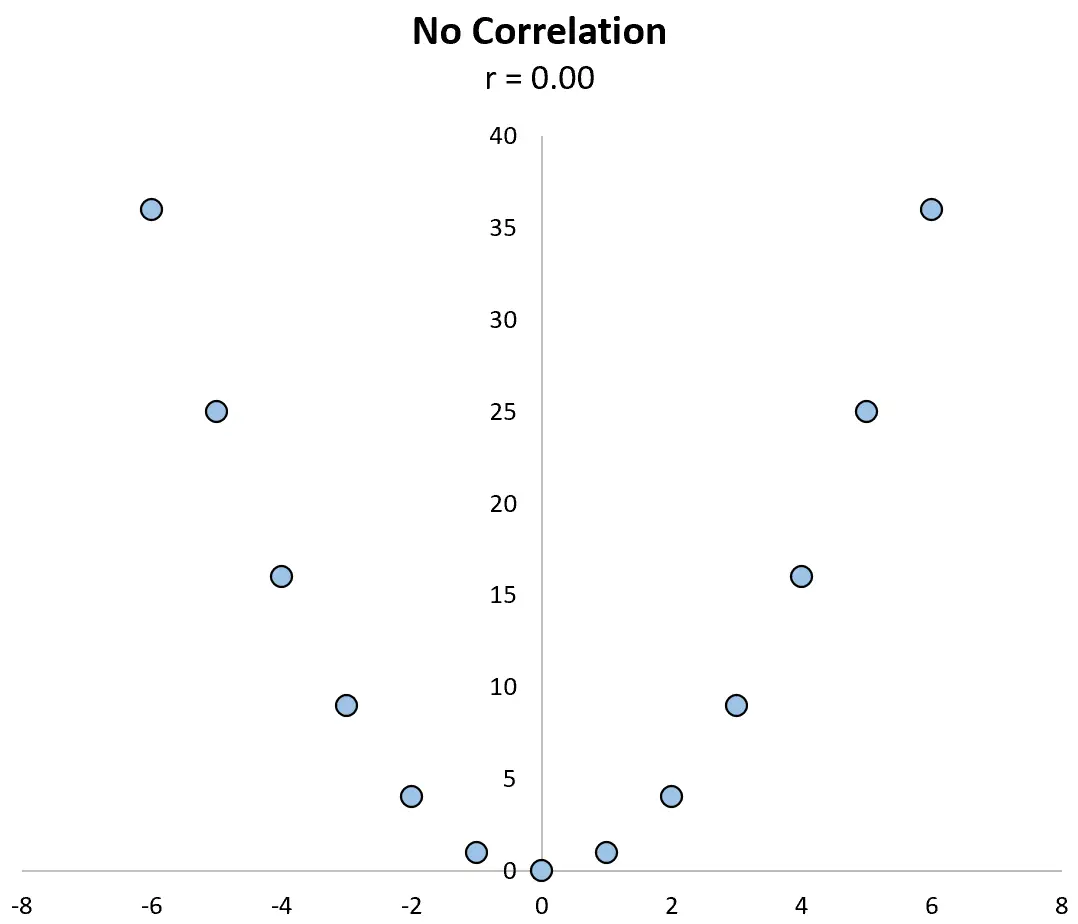
Переменные явно не имеют линейной связи, но у них есть нелинейная связь: значения y — это просто значения x, возведенные в квадрат.
Коэффициент корреляции сам по себе не мог обнаружить эту взаимосвязь, но диаграмма рассеяния могла.
Заключение
В итоге:
1. Как правило, коэффициент корреляции между 0,25 и 0,5 считается «слабой» корреляцией между двумя переменными.
2. Это практическое правило может варьироваться от региона к региону. Например, гораздо более низкая корреляция может считаться слабой в области медицины по сравнению с областью технологий. Обязательно используйте свои знания в предметной области, чтобы решить, что считать низкой корреляцией.
3. При использовании коэффициента корреляции для описания взаимосвязи между двумя переменными также полезно создать диаграмму рассеяния, чтобы можно было выявить выбросы в наборе данных, а также потенциальную нелинейную связь.
Дополнительные ресурсы
Что считается «сильной» корреляцией?
Калькулятор корреляционной матрицы
Корреляция против. ассоциация: в чем разница?