Как выполнить тест шеффе в sas
Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.
Если общее значение p таблицы ANOVA ниже определенного уровня значимости, то у нас есть достаточно доказательств, чтобы сказать, что по крайней мере одно из групповых средних значений отличается от других.
Однако это не говорит нам о том, какие группы отличаются друг от друга. Это просто говорит нам о том, что не все средние значения по группам одинаковы.
Чтобы точно узнать, какие группы отличаются друг от друга, нам нужно провести апостериорный тест .
Одним из наиболее часто используемых апостериорных тестов является тест Шеффе , который позволяет нам проводить попарные сравнения между средними значениями каждой группы, контролируя при этом частоту ошибок по семействам .
В следующем примере показано, как выполнить тест Шеффе в R.
Пример: тест Шеффе в SAS
Предположим, исследователь набирает 30 студентов для участия в исследовании. Студентам случайным образом назначаются использовать один из трех методов обучения для подготовки к экзамену.
Мы можем использовать следующий код для создания этого набора данных в SAS:
/*create dataset*/
data my_data;
input Method $Score;
datalines ;
At 76
At 77
At 77
At 81
At 82
At 82
At 83
At 84
At 85
At 89
B 81
B 82
B 83
B 83
B 83
B 84
B 87
B90
B92
B93
C 77
C 78
C 79
C 88
C 89
C 90
C 91
C 95
C 98
C 98
;
run ;
Далее мы будем использовать процедуру ANOVA для выполнения одностороннего дисперсионного анализа:
/*perform one-way ANOVA with Scheffe's post-hoc test*/
proc ANOVA data = my_data;
classMethod ;
modelScore = Method;
means Method / scheffe cldiff ;
run;
Примечание . Мы использовали оператор средних значений вместе с опциями Шеффе и Cldiff , чтобы указать, что апостериорный тест Шеффе должен выполняться (с доверительными интервалами), если общее значение p из однофакторного дисперсионного анализа является статистически значимым.
Сначала мы проанализируем таблицу ANOVA в результате:
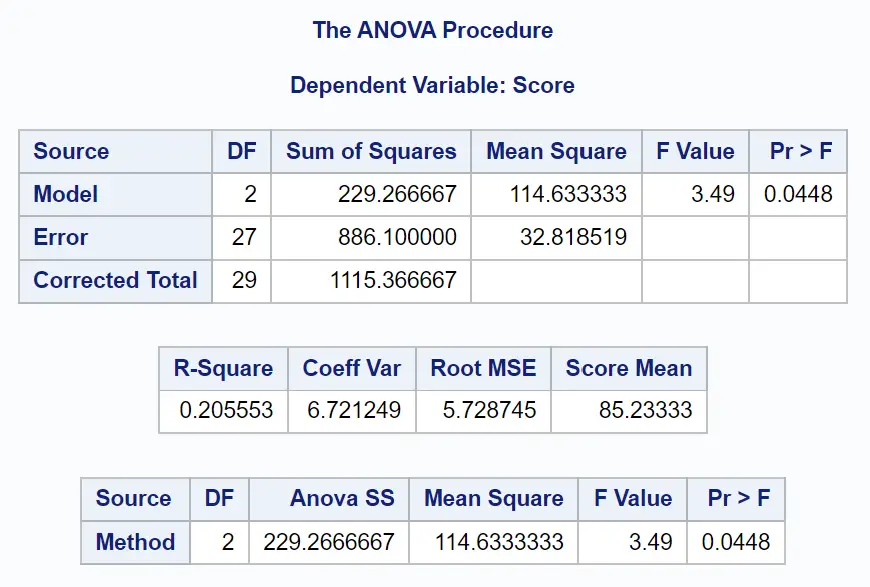
Из этой таблицы мы видим:
- Общее значение F: 3,49
- Соответствующее значение p: 0,0448.
Напомним, что однофакторный дисперсионный анализ использует следующие нулевые и альтернативные гипотезы:
- H 0 : Все средние значения группы равны.
- H A : По крайней мере одно среднее значение группы отличается отдых.
Поскольку значение p таблицы ANOVA (0,0448) меньше α = 0,05, мы отвергаем нулевую гипотезу.
Это говорит нам о том, что средний балл на экзамене не одинаков для всех трех методов обучения.
Связанный: Как интерпретировать F-значение и P-значение в ANOVA
Чтобы точно определить, какие групповые средние значения отличаются, нам нужно обратиться к окончательной таблице результатов, в которой показаны результаты апостериорных тестов Шеффе:
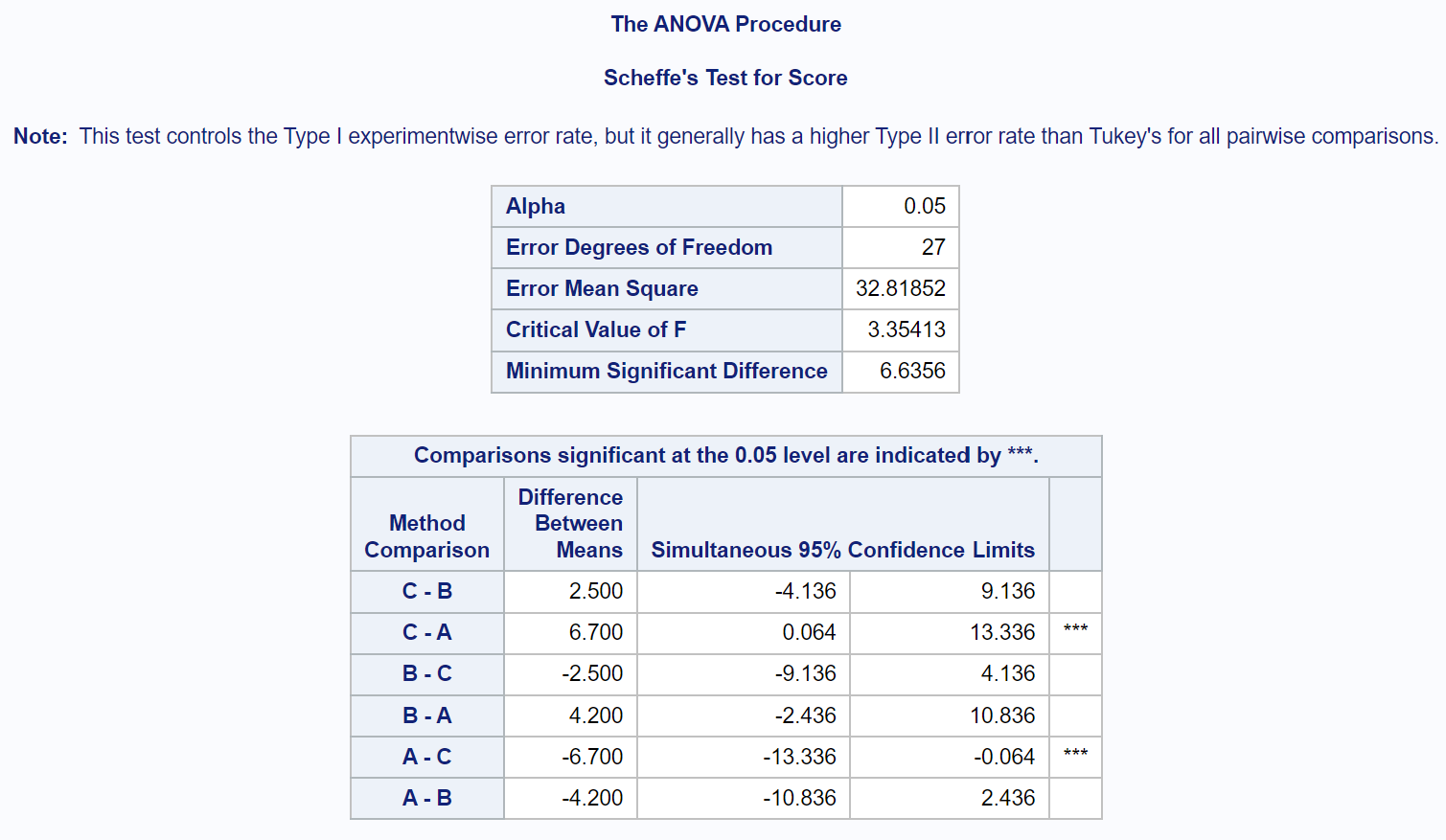
Чтобы выяснить, какие групповые средние значения различаются, нам нужно посмотреть, рядом с какими парными сравнениями стоят звездочки ( *** ).
Из таблицы видно, что существует статистически значимая разница в средних баллах экзамена между группой А и группой С.
Статистически значимых различий между средними значениями других групп нет.
В частности, мы видим, что средняя разница в экзаменационных баллах между группой C и группой A составляет 6,7 .
95% доверительный интервал для разницы средних значений между этими группами составляет [0,064, 13,336] .
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о моделях ANOVA:
Руководство по использованию апостериорного тестирования с помощью ANOVA
Как выполнить односторонний дисперсионный анализ в SAS
Как выполнить двусторонний дисперсионный анализ в SAS