Экспериментальная вероятность

Здесь вы узнаете, что такое экспериментальная вероятность и как рассчитывается экспериментальная вероятность. Дополнительно вы сможете увидеть пошагово решенный пример расчета экспериментальной вероятности.

Что такое экспериментальная вероятность?

Экспериментальная вероятность — это статистическая мера, основанная на результатах эксперимента или эмпирических фактах и указывающая на вероятность возникновения события.

Более того, чем чаще повторяется эксперимент, тем точнее будет полученная экспериментальная вероятность. По этой причине для определения вероятности эксперимента обычно используются компьютерные программы, способные быстро моделировать тысячи экспериментов, что обеспечивает более высокую точность.

Экспериментальная вероятность также известна как эмпирическая вероятность или частотная вероятность .

Экспериментальная вероятность — это число от 0 до 1. Логично, что чем больше значение экспериментальной вероятности события, тем более вероятно, что оно произойдет, и наоборот, чем меньше значение, тем менее вероятно, что оно произойдет. вполне вероятно, что произойдет. или событие происходит. Но значение экспериментальной вероятности всегда будет между нулем и единицей.

Экспериментальная формула вероятности

Формула экспериментальной вероятности представляет собой количество раз, когда событие произошло во время эксперимента, деленное на общее количество раз, когда эксперимент проводился.

Например, если человек бросает десять дротиков в мишень и ему удается поразить 6 дротиков в центре, вероятность того, что этот человек попадет дротик в центр, рассчитывается следующим образом:

Пример экспериментальной вероятности

Как только мы увидим математическое определение экспериментальной вероятности, мы решим пошаговое упражнение по этому типу вероятности. Цель состоит в том, чтобы вы узнали, как рассчитывается экспериментальная вероятность события, поэтому, если у вас есть вопросы, вы можете написать их в комментариях.

• Вычислите экспериментальную вероятность элементарных событий, составляющих случайный эксперимент по броску игральной кости.

Прежде чем найти экспериментальную вероятность, мы рассчитаем теоретическую вероятность, чтобы сравнить полученные экспериментальные результаты с теоретическими результатами. Как вы хорошо знаете, при броске игральной кости существует шесть возможных исходов (1, 2, 3, 4, 5 и 6), поэтому теоретическая вероятность каждого элементарного события равна:

Чтобы решить это упражнение, мы должны моделировать бросок игральной кости несколько раз и записать результаты в таблицу непредвиденных обстоятельств. В этом случае мы будем проводить моделирование с помощью программы Excel, но вы, очевидно, можете использовать программу по вашему выбору.

Сначала мы смоделируем десять бросков, затем сто бросков и, наконец, тысячу бросков. Таким образом, мы сможем проанализировать результаты и увидеть, как они меняются в зависимости от размера выборки эксперимента. Результаты, полученные после случайного моделирования 10 бросков игральных костей, следующие:

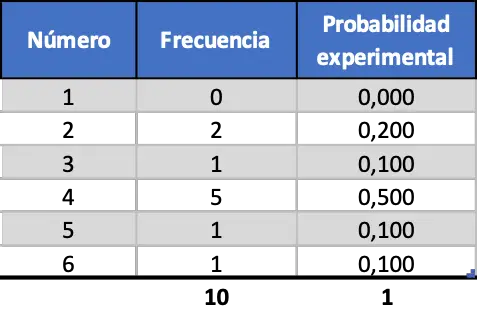
Как видите, полученные экспериментальные вероятности на данный момент сильно отличаются от рассчитанных ранее теоретических вероятностей (0,167).

Но по мере увеличения количества испытаний эти две метрики становятся более похожими, взгляните на симуляцию 100 запусков:

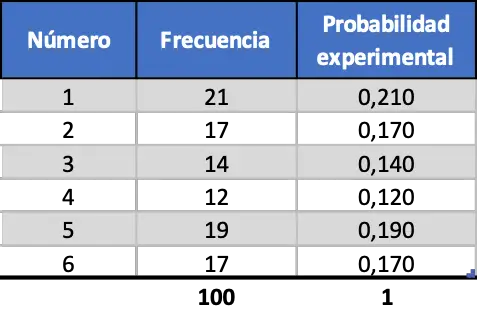
Теперь экспериментальная вероятность больше похожа на теоретическое значение вероятности, однако мы все равно получаем далекие значения.

Наконец, мы проделываем ту же процедуру, но моделируем 1000 запусков:

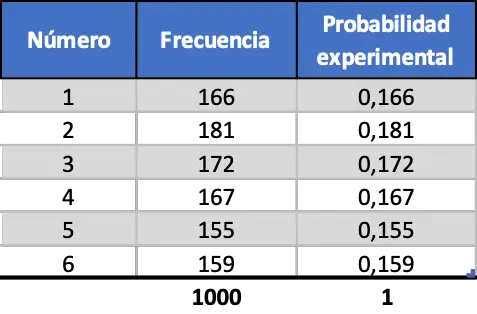
Как видно из последней таблицы сопряженности, теперь значения экспериментальных вероятностей очень похожи на теоретические вероятности.

Таким образом, чем больше количество проведенных экспериментов, тем ближе значение экспериментальной вероятности события будет к его теоретической вероятности . Это правило определяется как закон больших чисел , который гласит, что чем больше данных, тем ближе экспериментальные значения будут к теоретическим значениям.

Аналогично, если вы сравните три таблицы частот, вы увидите, что экспериментальная вероятность не является окончательной, а меняется в зависимости от количества проведенных экспериментов. А это значит, что вы должны знать, как интерпретировать полученные значения.

Экспериментальная вероятность и теоретическая вероятность

Разница между экспериментальной вероятностью и теоретической вероятностью (или классической вероятностью) заключается в том, что экспериментальная вероятность рассчитывается на основе данных, собранных в ходе реального эксперимента, тогда как теоретическая вероятность рассчитывается без необходимости проведения какого-либо эксперимента.

Как мы видели, нам необходимо смоделировать большое количество экспериментов, чтобы вывести экспериментальную вероятность события. Однако вычисление теоретической вероятности связано с теорией и логикой. Посмотреть, как это делается, можно здесь: