Экспоненциальная регрессия в r (шаг за шагом)

Экспоненциальная регрессия — это тип регрессии, который можно использовать для моделирования следующих ситуаций:

1. Экспоненциальный рост. Рост начинается медленно, а затем быстро и без ограничений ускоряется.

2. Экспоненциальный распад: распад начинается быстро, а затем замедляется, приближаясь все ближе и ближе к нулю.

Уравнение модели экспоненциальной регрессии имеет следующий вид:

у = аб ^х

Золото:

• y: переменная ответа
• x: прогнозируемая переменная
• a, b: коэффициенты регрессии, которые описывают взаимосвязь между x и y.

В следующем пошаговом примере показано, как выполнить экспоненциальную регрессию в R.

Шаг 1. Создайте данные

Во-первых, давайте создадим поддельные данные для двух переменных: x и y :

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

Шаг 2. Визуализируйте данные

Далее давайте создадим быструю диаграмму рассеяния, чтобы визуализировать связь между x и y :

 plot(x, y) 

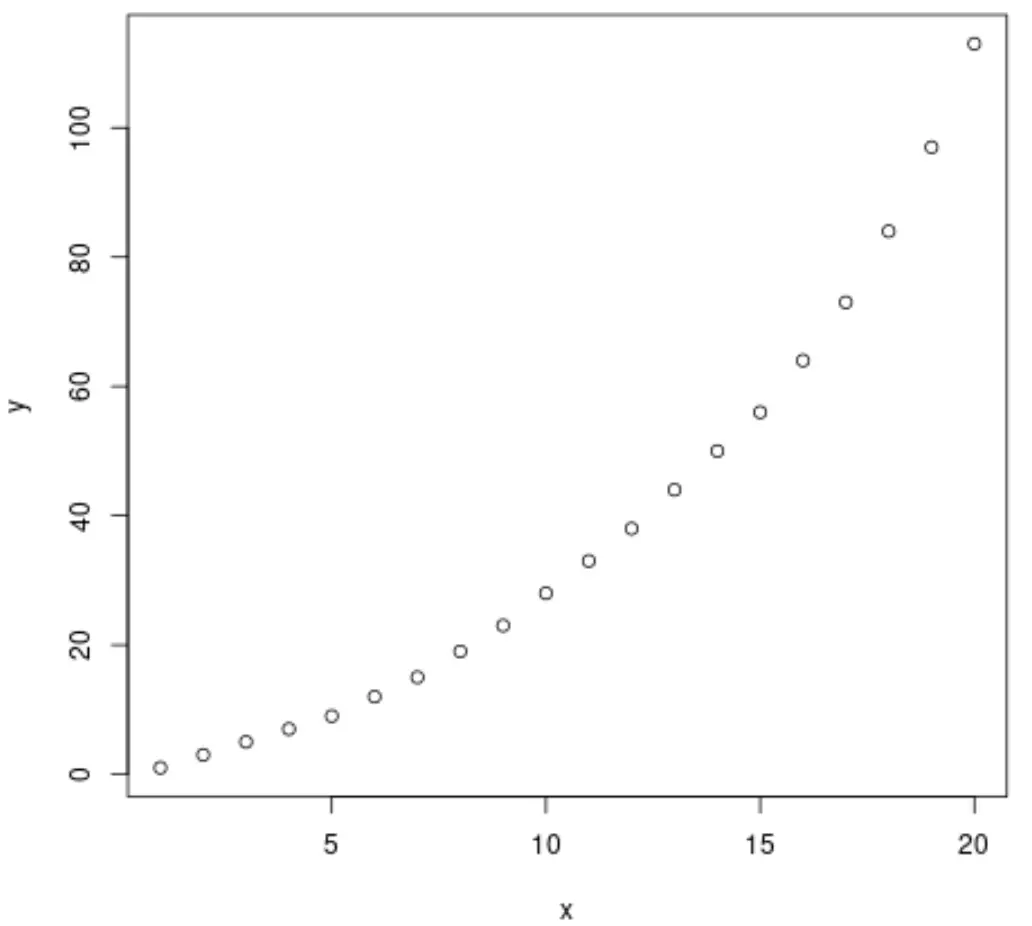
Из графика мы видим, что между двумя переменными существует четкая экспоненциальная модель роста.

Поэтому кажется разумным использовать уравнение экспоненциальной регрессии для описания взаимосвязи между переменными.

Шаг 3. Подберите модель экспоненциальной регрессии.

Далее мы будем использовать функцию lm() для соответствия модели экспоненциальной регрессии, используя натуральный логарифм y в качестве переменной отклика и x в качестве переменной-предиктора:

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

Общее значение F модели составляет 204, а соответствующее значение p чрезвычайно низкое (2,917e-11), что указывает на то, что модель в целом полезна.

Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение экспоненциальной регрессии имеет вид:

ln(y) = 0,9817 + 0,2041(x)

Применяя e к обеим частям, мы можем переписать уравнение следующим образом:

у = 2,6689 * ^1,2264x

Мы можем использовать это уравнение для прогнозирования переменной ответа y на основе значения переменной-предиктора x . Например, если x = 12, мы прогнозируем, что y будет 30,897 :

у = 2,6689 * 1,2264 ¹² = 30,897

Бонус: не стесняйтесь использовать этот онлайн-калькулятор экспоненциальной регрессии для автоматического расчета уравнения экспоненциальной регрессии для заданного предиктора и переменной отклика.

Дополнительные ресурсы

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить квадратичную регрессию в R
Как выполнить полиномиальную регрессию в R