Экспоненциальное распределение
В этой статье объясняется, что такое экспоненциальное распределение в статистике и для чего оно используется. Кроме того, вы узнаете, каковы свойства показательного распределения, а также его формулы, график и решенное упражнение. Кроме того, вы сможете вычислить любую вероятность с помощью онлайн-калькулятора экспоненциального распределения.
Что такое экспоненциальное распределение?
Экспоненциальное распределение — это непрерывное распределение вероятностей, используемое для моделирования времени ожидания возникновения случайного явления.
Точнее, экспоненциальное распределение позволяет нам описать время ожидания между двумя событиями, которое следует распределению Пуассона. Следовательно, экспоненциальное распределение тесно связано с распределением Пуассона.
Экспоненциальное распределение имеет характерный параметр, представленный греческой буквой λ и указывающий, сколько раз ожидаемое событие произойдет в течение заданного периода времени.
![]()
Аналогичным образом, экспоненциальное распределение также используется для моделирования времени до возникновения сбоя. Таким образом, экспоненциальное распределение имеет несколько приложений в теории надежности и выживания.
Примеры экспоненциальных распределений
Теперь, когда мы знаем определение экспоненциального распределения, давайте рассмотрим несколько примеров этого типа распределения, чтобы лучше понять эту концепцию.
Примеры экспоненциального распределения:
- Время, прошедшее между двумя звонками в колл-центр.
- Время, которое человек должен ждать, пока по определенной улице проедет бесплатное такси.
- Время ожидания, пока в магазин не зайдет новый покупатель.
- Время, которое проходит между двумя разными пользователями, заходящими на веб-страницу.
- В аэропорту прошло время между взлетом одного самолета и вылетом другого.
Формула экспоненциального распределения
Формула функции плотности, определяющая расчет вероятности экспоненциального распределения, равна λ, умноженному на число e в отрицательной степени λ, умноженное на x.
Другими словами, формула расчета вероятности экспоненциального распределения выглядит следующим образом:

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать вероятность переменной, которая подчиняется экспоненциальному распределению.
С другой стороны, формула для расчета кумулятивной вероятности экспоненциального распределения выглядит следующим образом:
![]()
График экспоненциального распределения
В этом разделе вы можете увидеть графическое представление функции плотности и функции распределения экспоненциального распределения.
Ниже вы можете увидеть, как меняется график функции плотности экспоненциального распределения в зависимости от значения параметра λ.
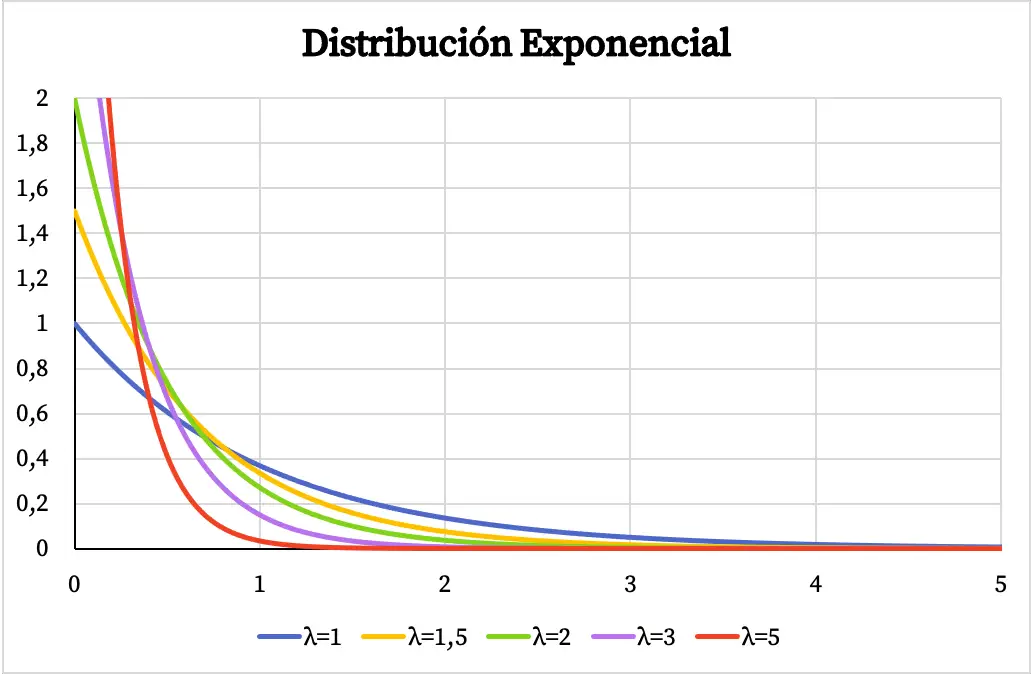
Аналогично, кумулятивная функция вероятности экспоненциального распределения также зависит от значения параметра λ, как вы можете видеть на следующем графике:
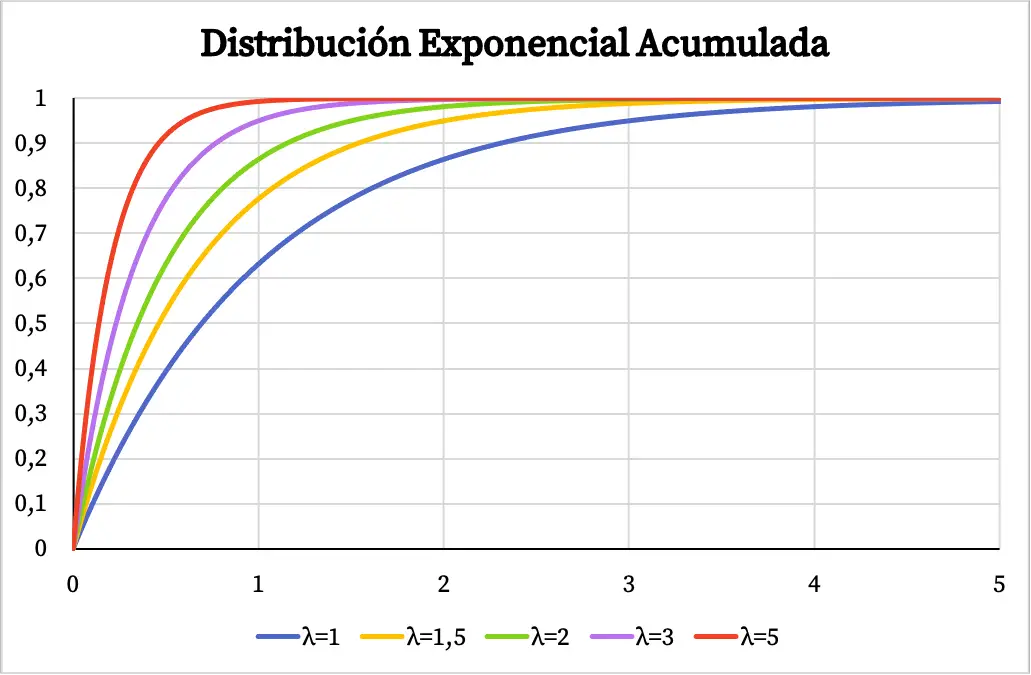
Решеное упражнение на показательное распределение
- В среднем λ=1 пользователей/мин посещают определенную веб-страницу. Какова вероятность того, что время между входом двух пользователей составит 3 минуты? А вероятность того, что оно равно или меньше 2 минут?
Распределение, определяющее случайную величину этой задачи, является экспоненциальным, поскольку мы изучаем время, которое проходит с момента возникновения события (захода пользователя на веб-страницу) до момента повторения этого же события.
![]()
Следовательно, чтобы вычислить вероятность того, что время, прошедшее между входом двух разных пользователей, составит три минуты, нам нужно применить формулу функции плотности (см. выше):
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4eb2d6e5190f313d74831763613683ec_l3.png)
С другой стороны, чтобы определить кумулятивную вероятность, мы должны использовать формулу функции распределения экспоненциального распределения:
![Rendered by QuickLaTeX.com \begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5ff6ef636fd31aec708b387669a68b93_l3.png)
Характеристики показательного распределения
Экспоненциальное распределение имеет следующие характеристики:
- Экспоненциальное распределение имеет характерный параметр λ, который указывает, сколько раз ожидается возникновение изучаемого явления в течение заданного периода времени.
![]()
- Экспоненциальное распределение не может принимать отрицательное значение, поэтому область экспоненциального распределения состоит из всех действительных чисел, больших или равных нулю.
![]()
- Среднее значение экспоненциального распределения равно единице, деленной на характеристический параметр λ.
![]()
- Дисперсия экспоненциального распределения равна квадрату его среднего значения, поэтому дисперсия экспоненциального распределения эквивалентна дисперсии коэффициента λ, возведенной в квадрат.
![]()
- Каким бы ни было значение λ, коэффициент асимметрии показательного распределения всегда равен 2.
![]()
- Аналогично, коэффициент эксцесса любого экспоненциального распределения всегда равен 9.
![]()
- Формула функции плотности экспоненциального распределения:
![]()
- В то время как формула кумулятивной функции вероятности экспоненциального распределения выглядит следующим образом:
![]()
- Экспоненциальное распределение — одно из немногих распределений вероятностей со свойством нехватки памяти. Это свойство означает, что возникновение предыдущего события не влияет на вероятность того, что это событие произойдет в будущем. Например, при экспоненциальном распределении вероятность того, что новый пользователь получит доступ к веб-странице менее чем за минуту, не зависит от того, вошел ли пользователь только что или с тех пор ни один пользователь не заходил. более десяти минут.
![P[X>x+y|X>y]=P[X>x]» title=»Rendered by QuickLaTeX.com» height=»19″ width=»254″ style=»vertical-align: -5px;»></p>
</p>
<h2 class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6f7c755e5b48eb203c51c97d7bc7ec7d_l3.png) Калькулятор экспоненциального распределения
Калькулятор экспоненциального распределения
Введите значение параметра λ и значение x в следующий калькулятор, чтобы рассчитать вероятность. Вам нужно выбрать вероятность, которую вы хотите рассчитать, и ввести числа, используя точку в качестве десятичного разделителя, например 0,50.