Эмпирическая вероятность

В этой статье мы объясним, как рассчитать эмпирическую вероятность. Вы узнаете, что такое эмпирическая вероятность, какова ее формула, пример и каковы различия между эмпирической вероятностью и теоретической вероятностью.

Что такое эмпирическая вероятность?

Эмпирическая вероятность — это статистическая мера, основанная на эмпирических экспериментах или фактах, которая указывает на вероятность возникновения события.

Другими словами, эмпирическая вероятность рассчитывается на основе результатов эксперимента и сообщает нам, насколько вероятно, что событие произойдет.

Чем больше повторяется эксперимент, тем точнее будет полученная эмпирическая вероятность. Вот почему этот тип вероятности обычно определяется с помощью компьютерных программ, моделирующих тысячи итераций и способных проанализировать их за очень короткое время.

Эмпирическая вероятность — это число от 0 до 1. Чем более вероятно событие, тем выше эмпирическая вероятность, и наоборот, чем менее вероятно событие, тем ниже его эмпирическая вероятность.

Эмпирическая формула вероятности

Формула эмпирической вероятности представляет собой количество раз, когда событие произошло во время эксперимента, деленное на общее количество раз, когда эксперимент проводился.

Например, если мы посмотрим на дерево десять раз и семь раз увидим на дереве птицу, эмпирическая вероятность увидеть птицу, глядя на дерево, будет равна:

Пример эмпирической вероятности

Учитывая определение эмпирической вероятности, мы решим пошаговое упражнение по этому типу вероятности. Таким образом, вы можете увидеть, как рассчитывается эмпирическая вероятность.

• Вычисляет эмпирическую вероятность элементарных событий, составляющих случайный эксперимент по броску игральной кости.

Сначала рассчитаем теоретическую вероятность сравнения полученных экспериментальных результатов с теоретическими результатами. При броске игральной кости существует шесть возможных исходов (1, 2, 3, 4, 5 и 6), поэтому теоретическая вероятность каждого элементарного события равна:

Чтобы решить это упражнение, мы должны моделировать бросок игральной кости несколько раз и записать результаты в таблицу непредвиденных обстоятельств. Для этого мы можем использовать, например, программу Excel.

Чтобы вы могли убедиться в важности количества проведенных экспериментов, мы сначала смоделируем десять запусков, затем сто и, наконец, тысячу. Таким образом, результаты, полученные в результате моделирования первых 10 случайных бросков игральной кости, следующие:

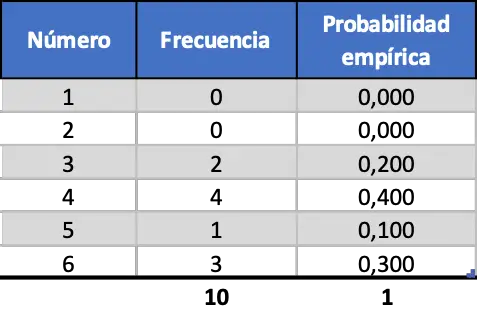
Как видите, эмпирические вероятности, полученные при моделировании всего десяти бросков, не близки к теоретическим вероятностям (0,167).

Но по мере увеличения количества экспериментов эти две метрики становятся более похожими, посмотрите на симуляцию 100 запусков:

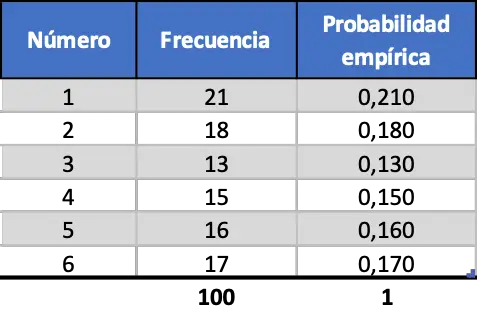
Теперь эмпирическая вероятность, рассчитанная для каждого числа на игральной кости, больше похожа на теоретическую вероятность, однако мы все равно получаем очень разные значения.

Наконец, мы проделываем ту же процедуру, но моделируем 1000 запусков:

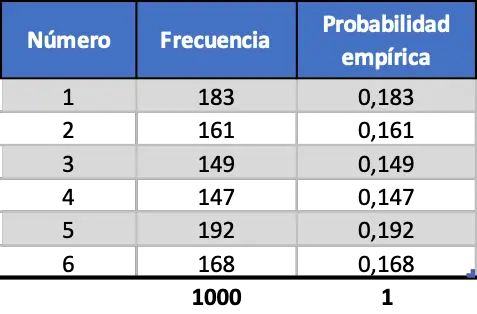
Как мы видим из последней таблицы сопряженности, теперь значения эмпирических вероятностей очень близки к теоретическим вероятностям.

Таким образом, чем больше мы увеличиваем количество проводимых экспериментов, тем ближе значение эмпирической вероятности события будет к его теоретической вероятности возникновения . Это правило определяется как закон больших чисел , который гласит, что чем больше данных, тем ближе экспериментальные значения будут к теоретическим значениям.

Более того, если мы сравним три таблицы частот, мы увидим, что эмпирическая вероятность не является окончательной, но меняется в зависимости от количества проведенных экспериментов. А это значит, что вы должны знать, как интерпретировать полученные значения.

Эмпирическая вероятность и теоретическая вероятность

Наконец, мы проанализируем понятия эмпирической вероятности и теоретической вероятности, поскольку, хотя это два типа вероятностей, они имеют совершенно разное значение.

Разница между эмпирической вероятностью и теоретической вероятностью (или классической вероятностью) состоит в том, что эмпирическая вероятность рассчитывается на основе данных, собранных на основе реального опыта, тогда как теоретическая вероятность рассчитывается с учетом идеальных обстоятельств без проведения какого-либо эксперимента.

То есть, чтобы найти эмпирическую вероятность, необходимо смоделировать эксперимент и провести расчет на основе полученных результатов. Но чтобы узнать теоретическую вероятность, необходимо проводить не эксперимент, а теоретический расчет.

Кроме того, уровень систематической ошибки определяется как разница между эмпирической вероятностью и теоретической вероятностью. Смещение может быть положительным или отрицательным, но очень трудно добиться того, чтобы оно было равно нулю, потому что это означало бы, что случайный эксперимент просто соответствует теоретической вероятности, что очень маловероятно.