Тест бреуша-пэгана: определение и пример
Одним из ключевых предположений линейной регрессии является то, что остатки распределяются с одинаковой дисперсией на каждом уровне переменной-предиктора. Это предположение известно как гомоскедастичность .
Если это предположение не соблюдается, говорят, что в остатках присутствует гетероскедастичность . Когда это происходит, результаты регрессии становятся ненадежными.
Один из способов визуально определить наличие гетероскедастичности — создать график остатков в зависимости от подобранных значений из регрессионной модели.
Если остатки разбросаны больше при более высоких значениях на графике, это явный признак наличия гетероскедастичности.
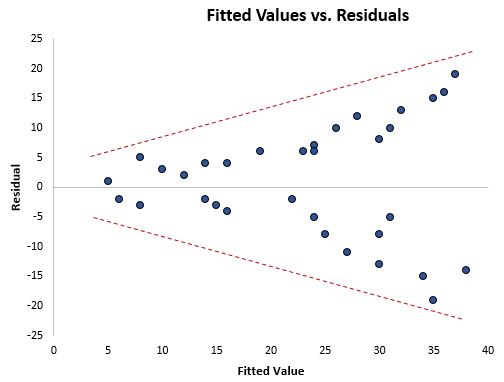
Формальным статистическим тестом, который мы можем использовать для определения наличия гетероскедастичности, является тест Бреуша-Пэгана .
В этом руководстве представлено краткое объяснение теста Бреуша-Пэгана вместе с примером.
Что такое тест Бреуша-Пэгана?
Тест Бреуша-Пэгана используется для определения наличия гетероскедастичности в регрессионной модели.
В тесте используются следующие нулевые и альтернативные гипотезы :
- Нулевая гипотеза (H 0 ): гомоскедастичность присутствует (остатки распределяются с равной дисперсией)
- Альтернативная гипотеза ( HA ): присутствует гетероскедастичность (остатки не распределяются с одинаковой дисперсией)
Если значение p теста ниже определенного уровня значимости (т. е. α = 0,05), то мы отвергаем нулевую гипотезу и заключаем, что гетероскедастичность присутствует в регрессионной модели.
Для проведения теста Бреуша-Пэгана мы используем следующие шаги:
1. Подберите регрессионную модель.
2. Рассчитайте квадраты остатков модели.
3. Подберите новую модель регрессии, используя квадраты остатков в качестве значений ответа.
4. Рассчитайте статистику критерия Хи-квадрат X 2 в форме n*R 2 new , где:
- n: Общее количество наблюдений
- R 2 new : R-квадрат новой регрессионной модели, в которой в качестве значений ответа использовались квадраты остатков.
Если значение p, соответствующее этой статистике критерия хи-квадрат со степенями свободы p (количество предикторов), ниже определенного уровня значимости (т. е. α = 0,05), тогда отклоните нулевую гипотезу и сделайте вывод о наличии гетероскедастичности. .
В противном случае не отвергайте нулевую гипотезу. В этом случае предполагается наличие гомоскедастичности.
Обратите внимание, что большинство статистических программ могут легко выполнить тест Бреуша-Пэгана, поэтому вам, вероятно, никогда не придется выполнять эти шаги вручную, но полезно знать, что происходит за кулисами.
Пример теста Бреуша-Пэгана
Предположим, у нас есть следующий набор данных, содержащий информацию о 10 разных баскетболистах:
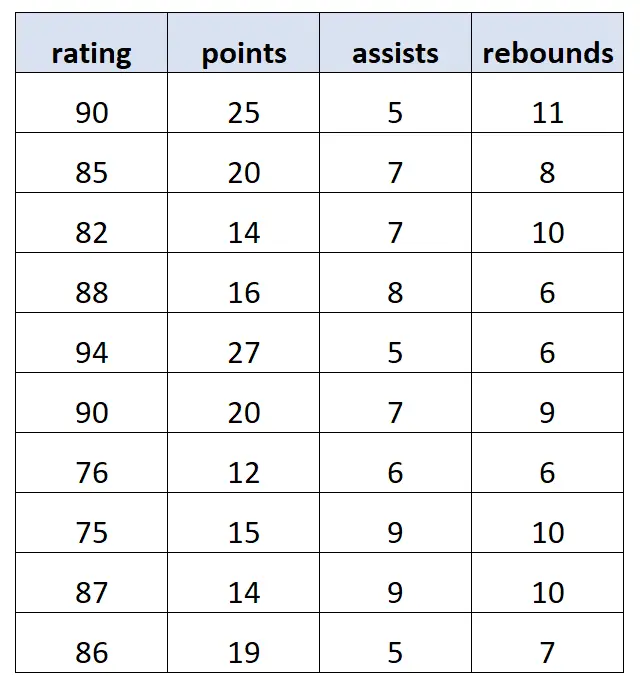
Используя статистическое программное обеспечение, мы подогнали следующую модель множественной линейной регрессии :
счет = 62,47 + 1,12*(очки) + 0,88*(передачи) – 0,43*(подборы)
Затем мы используем эту модель для прогнозирования рейтинга каждого игрока и расчета квадратов остатков (т. е. разницы в квадрате между прогнозируемым рейтингом и фактическим рейтингом):
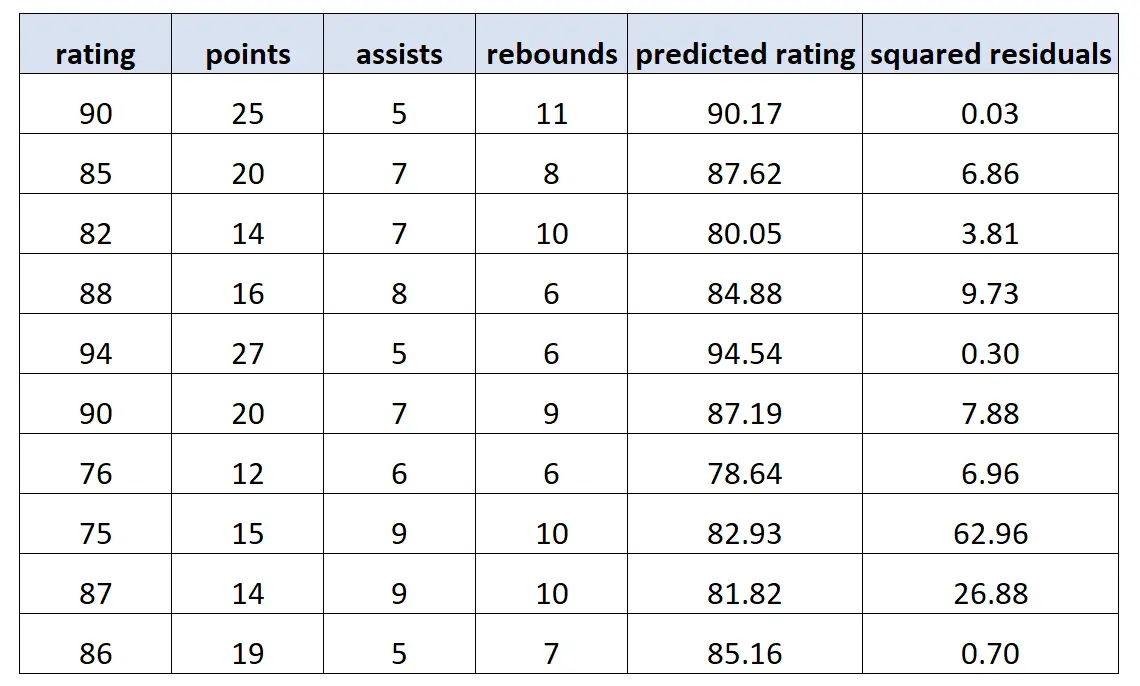
Затем мы подгоняем новую модель регрессии, используя квадраты остатков в качестве значений ответа и исходные переменные-предикторы в качестве переменных-предикторов еще раз. Мы находим следующее:
- н: 10
- Р 2 новый : 0,600395
Итак, наша статистика критерия Хи-квадрат для теста Бреуша-Пэгана равна n*R 2 new = 10*.600395 = 6,00395 . Степени свободы представляют собой p = 3 переменных-предиктора.
Согласно калькулятору значения хи-квадрат для P , значение p, которое соответствует X 2 = 6,00395 с 3 степенями свободы, составляет 0,111418 .
Поскольку это значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Поэтому мы предполагаем, что гомоскедастичность присутствует.
Тест Бреуша-Пагана на практике
В следующих руководствах представлены пошаговые примеры выполнения теста Бреуша-Пагана в различных статистических программах:
Как выполнить тест Бреуша-Пагана в Excel
Как выполнить тест Бреуша-Пэгана в R
Как выполнить тест Бреуша-Пэгана в Python
Как выполнить тест Бреуша-Пагана в Stata