วิธีสร้างพล็อตที่เหลือใน python

พล็อตส่วนที่เหลือ เป็นประเภทของพล็อตที่แสดงค่าที่พอดีเทียบกับส่วนที่เหลือของ แบบจำลองการถดถอย

พล็อตประเภทนี้มักใช้ในการประเมินว่าแบบจำลองการถดถอยเชิงเส้นมีความเหมาะสมสำหรับชุดข้อมูลที่กำหนดหรือไม่ และเพื่อตรวจสอบค่าคงเหลือสำหรับ ค่าเฮเทอโรสเคดาสติกซิตี

บทช่วยสอนนี้จะอธิบายวิธีสร้างพล็อตที่เหลือสำหรับโมเดลการถดถอยเชิงเส้นใน Python

ตัวอย่าง: พล็อตที่เหลือใน Python

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูลที่อธิบายคุณสมบัติของผู้เล่นบาสเก็ตบอล 10 คน:

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

พล็อตคงเหลือสำหรับการถดถอยเชิงเส้นอย่างง่าย

สมมติว่าเราปรับโมเดลการถดถอยเชิงเส้นอย่างง่ายโดยใช้ จุด เป็นตัวแปรทำนายและ เกรด เป็นตัวแปรตอบสนอง:

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

เราสามารถสร้างพล็อตที่เหลือหรือพอดีได้โดยใช้ ฟังก์ชัน plot_regress_exog() จากไลบรารี statsmodels:

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

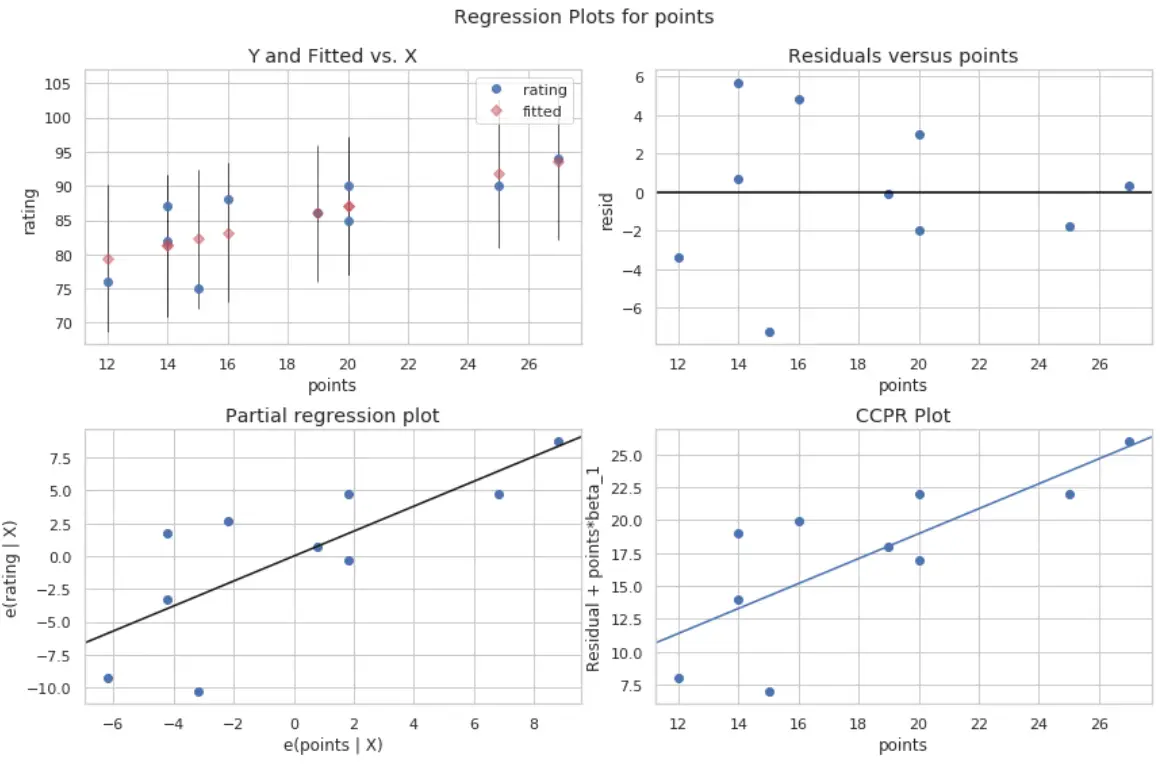
มีการผลิตสี่แปลง อันที่มุมขวาบนคือพล็อตที่เหลือเทียบกับพล็อตที่ปรับแล้ว แกน x บนพล็อตนี้แสดงค่าที่แท้จริงของ จุด ตัวแปรทำนายและแกน y จะแสดงค่าคงเหลือสำหรับค่านั้น

เนื่องจากส่วนที่เหลือดูเหมือนจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์ นี่บ่งชี้ว่าความต่างกันไม่เป็นปัญหากับตัวแปรทำนาย

แปลงคงเหลือสำหรับการถดถอยเชิงเส้นพหุคูณ

สมมติว่าเราปรับโมเดลการถดถอยเชิงเส้นหลายตัวแทนโดยใช้ การช่วย และ การรีบาวด์ เป็นตัวแปรทำนายและ การจัดอันดับ เป็นตัวแปรตอบสนอง:

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

อีกครั้งที่เราสามารถสร้างพล็อตที่เหลือเทียบกับตัวทำนายสำหรับตัวทำนายแต่ละตัวโดยใช้ ฟังก์ชัน plot_regress_exog() จากไลบรารี statsmodels

ตัวอย่างเช่น นี่คือลักษณะของพล็อตส่วนที่เหลือ/ตัวทำนายสำหรับ การช่วยเหลือ ตัวแปรตัวทำนาย :

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

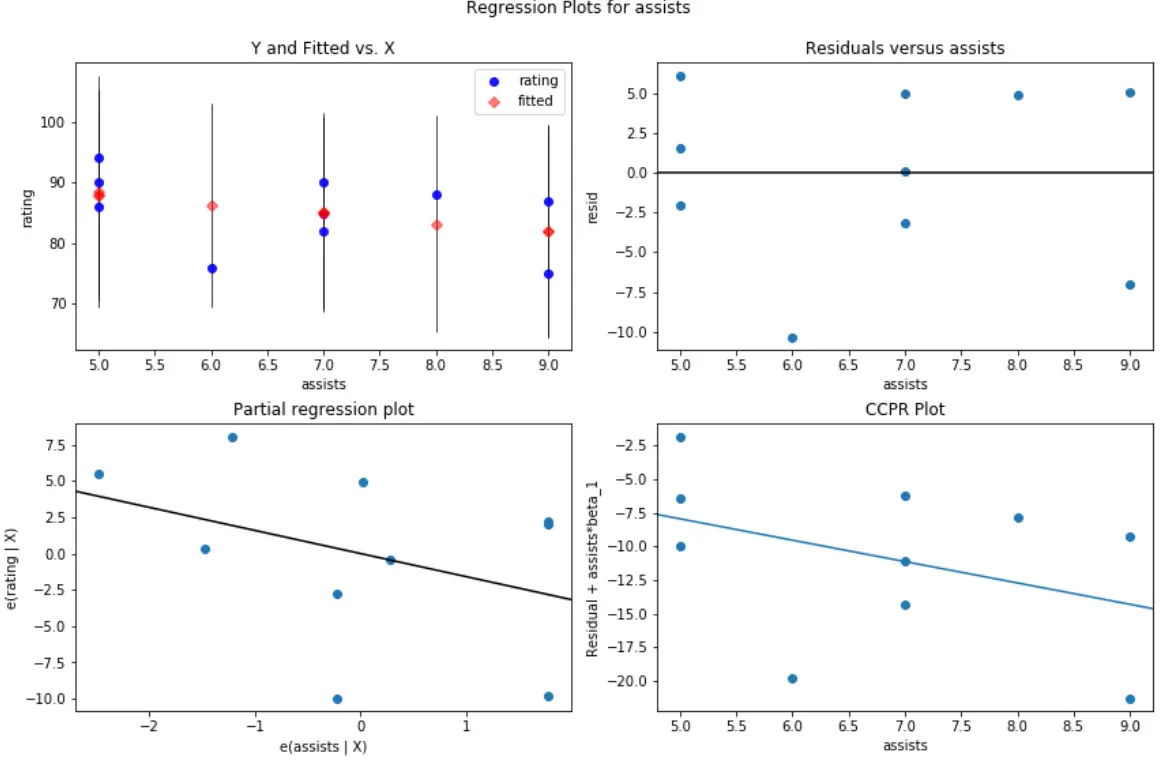
และนี่คือลักษณะของพล็อตส่วนที่เหลือ/ตัวทำนายสำหรับตัวแปรตัวทำนายที่ ตีกลับ :

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

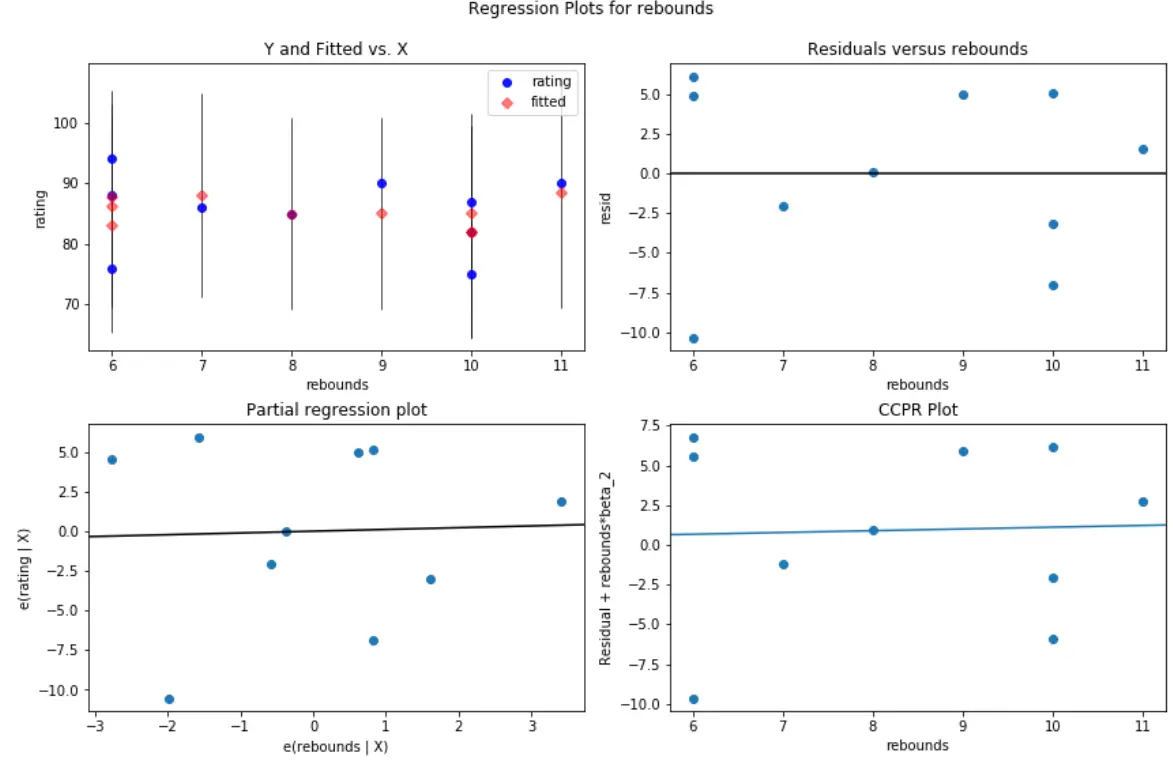
ในทั้งสองแปลง ส่วนที่เหลือดูเหมือนจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์ ซึ่งบ่งชี้ว่าความต่างกันไม่เป็นปัญหากับตัวแปรทำนายใดๆ ในแบบจำลอง