การกระจายตัวของนักเรียน

โดย สิงหาคม 4, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจง Student t คืออะไร และใช้เพื่ออะไร นอกจากนี้ จะแสดงกราฟของการแจกแจงค่า t ของนักเรียน และลักษณะเฉพาะของการแจกแจงความน่าจะเป็นประเภทนี้

การกระจายตัวของนักเรียนคืออะไร?

การแจกแจงของนักเรียน เป็นการแจกแจงความน่าจะเป็นที่ใช้กันอย่างแพร่หลายในสถิติ โดยเฉพาะอย่างยิ่ง การแจกแจงค่า t ของนักเรียนจะใช้ในการทดสอบ t ของนักเรียนเพื่อหาความแตกต่างระหว่างค่าเฉลี่ยของสองตัวอย่างและเพื่อสร้างช่วงความเชื่อมั่น

การแจกแจงของนักเรียนได้รับการพัฒนาโดยนักสถิติ William Sealy Gosset ในปี 1908 โดยใช้นามแฝงว่า “Student”

การแจกแจงค่า t ของนักเรียนถูกกำหนดโดยจำนวนระดับความอิสระ ซึ่งได้มาจากการลบหนึ่งหน่วยออกจากจำนวนการสังเกตทั้งหมด ดังนั้น สูตรในการกำหนดระดับความเป็นอิสระของการแจกแจงแบบ t ของนักเรียนคือ ν=n-1

\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}

กราฟการกระจายตัวของนักเรียน

ตอนนี้เรารู้คำจำกัดความของการแจกแจงแบบ t ของนักเรียนแล้ว เรามาดูกันว่ากราฟของมันคืออะไร ด้านล่างนี้ คุณจะเห็นตัวอย่างการแจกแจง t ของนักเรียนที่มีระดับความเป็นอิสระต่างกันเป็นภาพกราฟิก

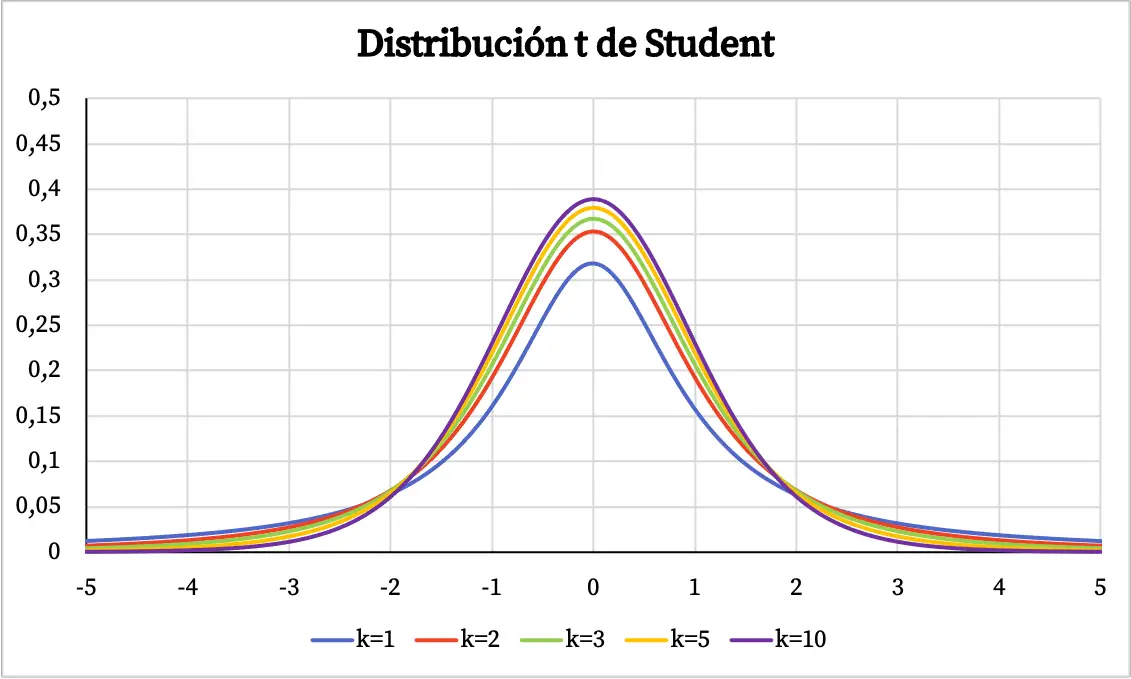
กราฟการกระจายตัวของนักเรียน

จากกราฟของการแจกแจงค่า t ของนักเรียน สามารถสรุปคุณสมบัติต่อไปนี้ได้:

  • การแจกแจงของนักเรียนมีศูนย์กลางสมมาตรที่ 0 และมีรูปร่างระฆัง
  • การแจกแจงแบบ t ของนักเรียนจะกระจายมากกว่าการแจกแจงแบบปกติ กล่าวคือ เส้นโค้งของการแจกแจงแบบ t ของนักเรียนจะกว้างกว่า
  • ยิ่งการกระจายค่า t ของนักเรียนมีระดับอิสระมากเท่าใด การกระจายตัวของนักเรียนก็จะยิ่งน้อยลงเท่านั้น

ในกราฟด้านบน ฟังก์ชันความหนาแน่นของการแจกแจงแบบ t ของนักเรียนได้ถูกพล็อตเทียบกับระดับความอิสระของมัน อย่างไรก็ตาม คุณจะเห็นด้านล่างว่าฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบ t ของนักเรียนแตกต่างกันอย่างไร:

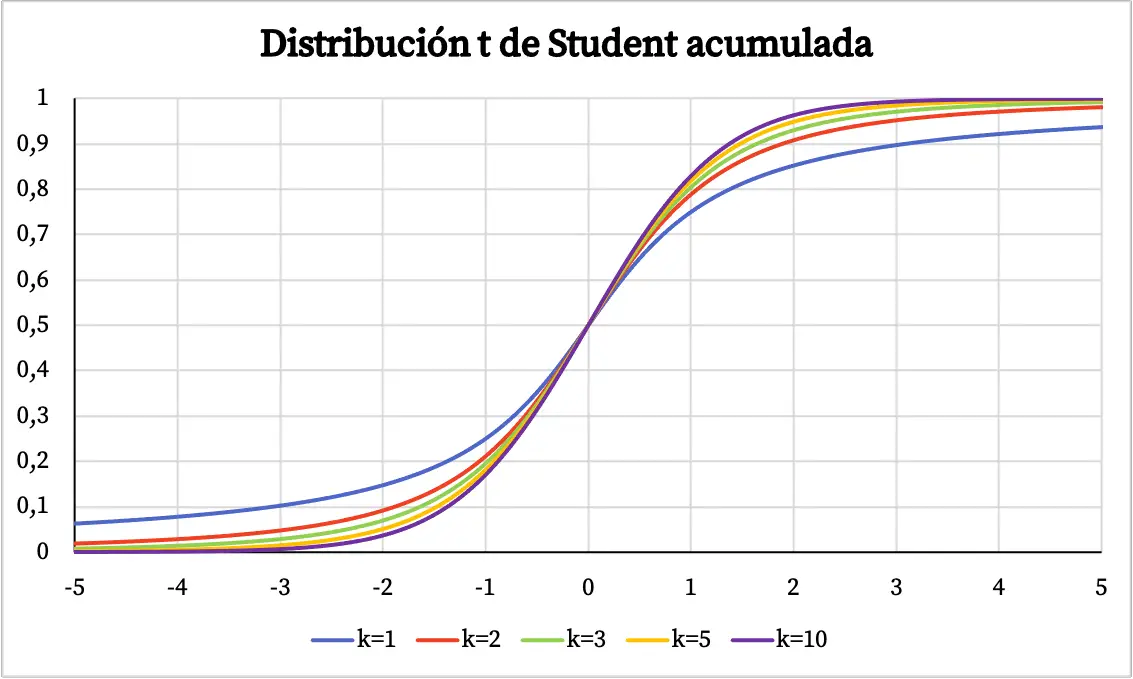
โครงเรื่องของการแจกแจงค่า t สะสมของนักเรียน

ลักษณะการกระจายตัวของนักเรียน

ลักษณะที่สำคัญที่สุดของการแจกแจงค่า t ของนักเรียนมีดังต่อไปนี้

  • โดเมนของการแจกแจง Student t ประกอบด้วยจำนวนจริง

x\in (-\infty, +\infty)

  • สำหรับการแจกแจงแบบ t ของนักเรียนที่มีระดับความเป็นอิสระมากกว่าหนึ่งระดับ ค่าเฉลี่ยของการแจกแจงจะเท่ากับ 0

\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p> </p> <ul> <li> ความแปรปรวนของการแจกแจงแบบ t ของนักเรียนสามารถคำนวณได้โดยใช้นิพจน์ต่อไปนี้</li> </ul> <p class=\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p> </p> <ul> <li> ค่ามัธยฐานและรูปแบบการแจกแจงแบบ t ของนักเรียน โดยไม่คำนึงถึงจำนวนระดับความเป็นอิสระจะเป็น 0 เสมอ</li> </ul> <p class=\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}

  • ฟังก์ชันความหนาแน่นของการแจกแจง Student t ถูกกำหนดโดยสูตรต่อไปนี้:

\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}

  • ฟังก์ชันการแจกแจงความน่าจะเป็นสะสมของการแจกแจงแบบ t ถูกกำหนดโดยสูตรต่อไปนี้:

\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}

  • สำหรับการแจกแจงค่า t ของนักเรียนที่มีดีกรีอิสระมากกว่า 3 ค่าสัมประสิทธิ์ความไม่สมมาตรจะเป็นศูนย์เนื่องจากเป็นการแจกแจงแบบสมมาตร

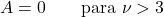
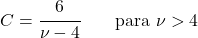\displaystyle A=0\qquad \text{para }\nu>3″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”164″ style=”vertical-align: -4px;”></p> </p> <ul> <li> หากระดับความอิสระของการแจกแจงค่า t ของนักเรียนมากกว่า 4 ความโด่งสามารถคำนวณได้โดยการหาร 6 ด้วยระดับความอิสระลบด้วย 4 </li> </ul> <p class=\displaystyle C=\cfrac{6}{\nu-4}\qquad \text{para }\nu>4″ title=”Rendered by QuickLaTeX.com” height=”38″ width=”198″ style=”vertical-align: -12px;”></p> </p> <h2 class= การประยุกต์ใช้การกระจายตัวของนักเรียน

การแจกแจงของนักเรียนเป็นการแจกแจงความน่าจะเป็นที่ใช้กันอย่างแพร่หลายในสถิติ ในความเป็นจริง มีแม้กระทั่งการทดสอบของนักเรียน ซึ่งใช้เพื่อทดสอบสมมติฐานและช่วงความเชื่อมั่น

ดังนั้น การแจกแจงค่า t ของนักเรียนช่วยให้เราวิเคราะห์ความแตกต่างระหว่างค่าเฉลี่ยของสองตัวอย่างได้ และแม่นยำยิ่งขึ้น โดยใช้เพื่อพิจารณาว่าสองตัวอย่างมีค่าเฉลี่ยที่แตกต่างกันอย่างมีนัยสำคัญหรือไม่ ในทำนองเดียวกัน การทดสอบของนักเรียนใช้เพื่อค้นหาว่าเส้นที่ได้จากการวิเคราะห์การถดถอยเชิงเส้นมีความชันหรือไม่

กล่าวโดยสรุป การประยุกต์ใช้การแจกแจงแบบนักเรียนจะขึ้นอยู่กับการวิเคราะห์ชุดข้อมูลที่เป็นไปตามทฤษฎีการแจกแจงแบบปกติ แต่จำนวนการสังเกตทั้งหมดน้อยเกินไปที่จะใช้การแจกแจงประเภทนี้

เกี่ยวกับผู้แต่ง

Dr. Benjamin Anderson
ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

เพิ่มความคิดเห็น

อีเมลของคุณจะไม่แสดงให้คนอื่นเห็น ช่องข้อมูลจำเป็นถูกทำเครื่องหมาย *