ความรู้เบื้องต้นเกี่ยวกับการแจกแจงพหุนาม
การแจกแจงแบบพหุนาม อธิบายความน่าจะเป็นของการนับจำนวนเฉพาะสำหรับผลลัพธ์ที่แตกต่างกัน k รายการ เมื่อแต่ละผลลัพธ์มีความน่าจะเป็นคงที่ที่จะเกิดขึ้น
หาก สามารถหา ตัวแปร สุ่ม _ ได้จากสูตรต่อ ไป นี้:
ความน่าจะเป็น = ไม่มี! * (หน้า 1 x 1 * หน้า 2 x 2 * … * หน้า x k ) / (x 1 ! * x 2 ! … * x k !)
ทอง:
- n: จำนวนเหตุการณ์ทั้งหมด
- x 1 : จำนวนครั้งที่ผลลัพธ์ 1 เกิดขึ้น
- p 1 : ความน่าจะเป็นที่ผลลัพธ์ 1 เกิดขึ้นในการทดลองที่กำหนด
ตัวอย่างเช่น สมมติว่ามีลูกหินสีแดง 5 ลูก ลูกหินสีเขียว 3 ลูก และลูกหินสีฟ้า 2 ลูกในโกศ หากเราสุ่มหยิบลูกหิน 5 ลูกจากโกศ โดยแทนที่ ความน่าจะเป็นที่จะได้ลูกหินสีแดง 2 ลูก ลูกหินสีเขียว 2 ลูก และลูกหินสีน้ำเงิน 1 ลูก เป็นเท่าใด
เพื่อตอบคำถามนี้ เราสามารถใช้การแจกแจงพหุนามด้วยพารามิเตอร์ต่อไปนี้:
- น : 5
- x 1 (# ลูกหินสีแดง) = 2, x 2 (# ลูกหินสีเขียว) = 2, x 3 (# ลูกหินสีน้ำเงิน) = 1
- p 1 (ปัญหาสีแดง) = 0.5, p 2 (ปัญหาสีเขียว) = 0.3, p 3 (ปัญหาสีน้ำเงิน) = 0.2
เมื่อแทนตัวเลขเหล่านี้ลงในสูตร เราพบว่าความน่าจะเป็นคือ:
ความน่าจะเป็น = 5! * (.5 2 * .3 2 * .2 1 ) / (2! * 2! * 1!) = 0.135 .
ปัญหาการฝึกการกระจายพหุนาม
ใช้แบบฝึกหัดแก้ปัญหาต่อไปนี้เพื่อทดสอบความรู้เกี่ยวกับการแจกแจงพหุนาม
หมายเหตุ: เราจะใช้ เครื่องคำนวณการกระจายพหุนาม เพื่อคำนวณคำตอบของคำถามเหล่านี้
ปัญหาที่ 1
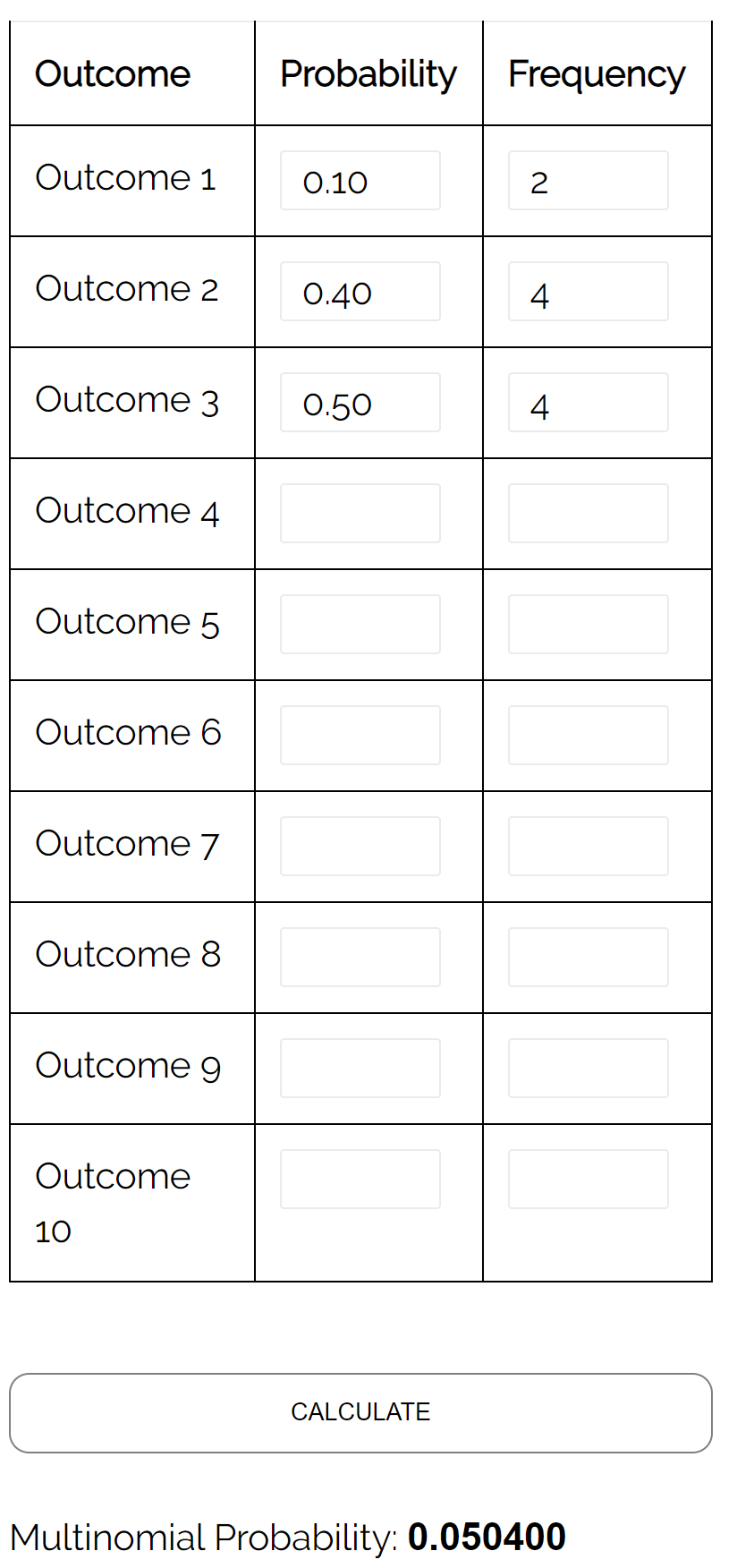
คำถาม: ในการเลือกตั้งนายกเทศมนตรีแบบสามทาง ผู้สมัคร A จะได้รับคะแนนเสียง 10% ผู้สมัคร B จะได้รับคะแนนเสียง 40% และผู้สมัคร C จะได้รับคะแนนเสียง 50% หากเราสุ่มตัวอย่างผู้ลงคะแนนเสียง 10 คน ความน่าจะเป็นที่ 2 คนโหวตให้ผู้สมัคร A, 4 คนโหวตให้ผู้สมัคร B และ 4 คนโหวตให้ผู้สมัคร C เป็นเท่าใด
คำตอบ: การใช้เครื่องคำนวณการกระจายพหุนามกับอินพุตต่อไปนี้ เราพบว่าความน่าจะเป็นคือ 0.0504:
ปัญหาที่ 2
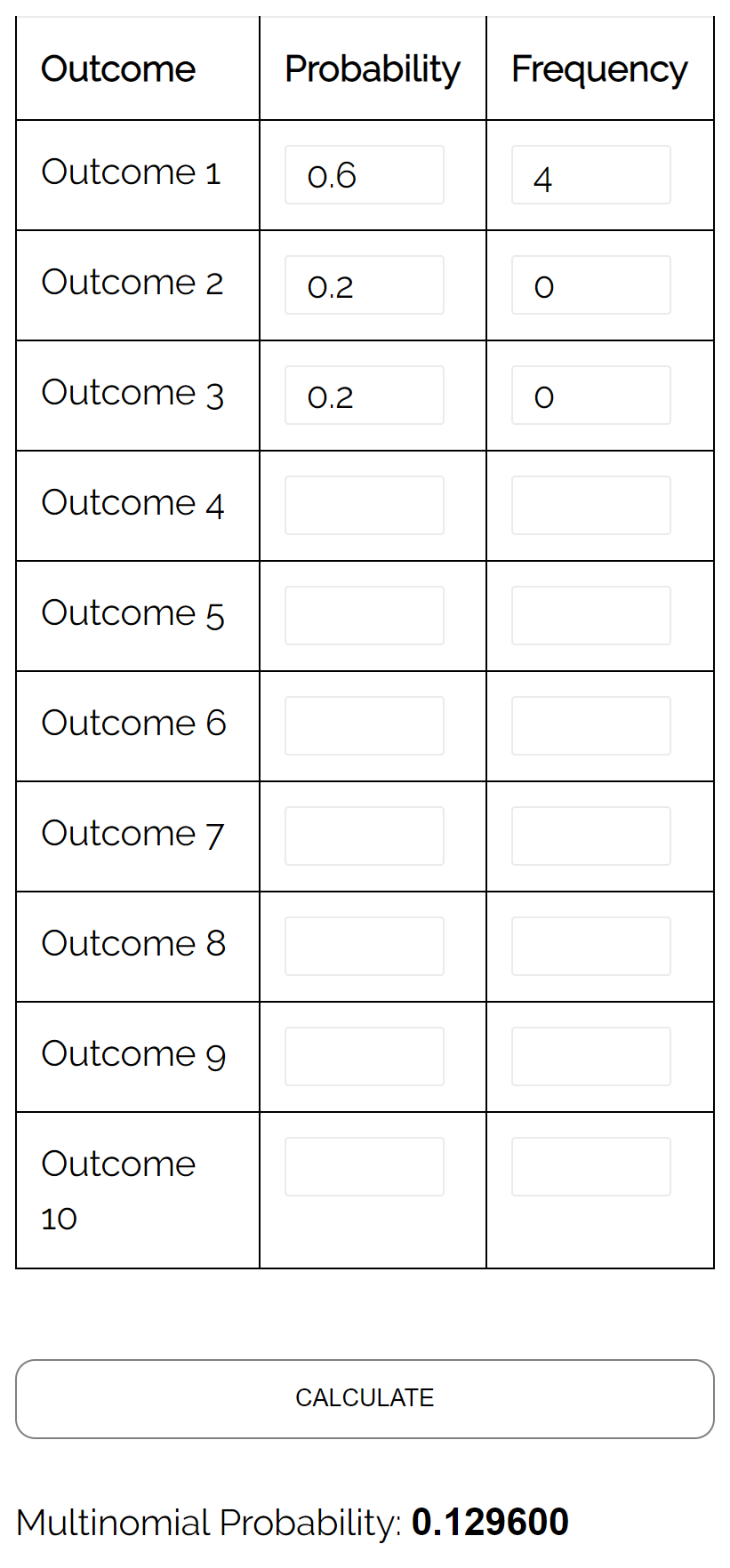
คำถาม: สมมติว่าโกศประกอบด้วยลูกหินสีเหลือง 6 ลูก ลูกหินสีแดง 2 ลูก และลูกหินสีชมพู 2 ลูก ถ้าเราสุ่มเลือกลูกบอล 4 ลูกจากโกศมาแทนที่ ความน่าจะเป็นที่ลูกบอลทั้ง 4 ลูกจะเป็นสีเหลืองเป็นเท่าใด
คำตอบ: การใช้เครื่องคำนวณการกระจายพหุนามกับอินพุตต่อไปนี้ เราพบว่าความน่าจะเป็นคือ 0.1296:
ปัญหา 3
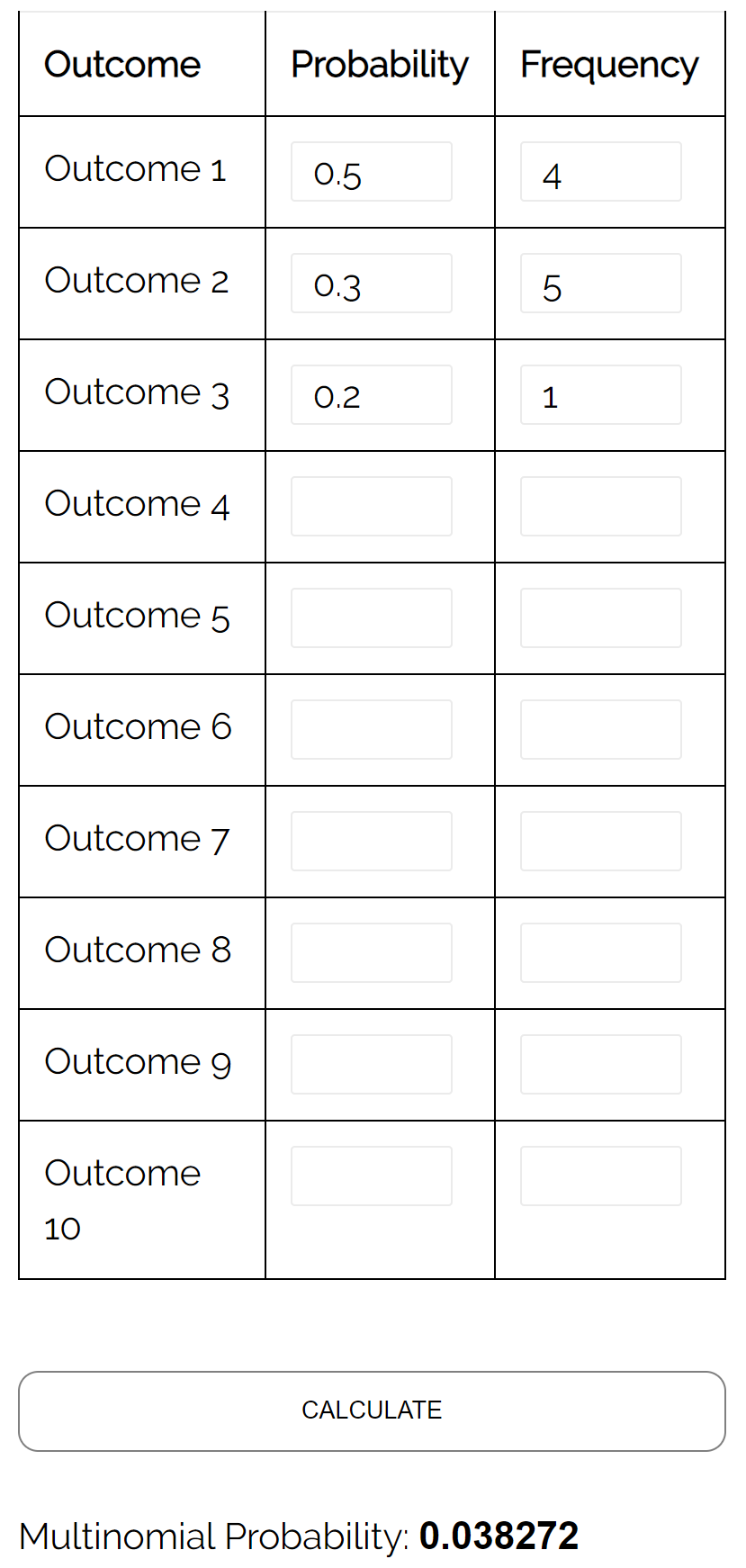
คำถาม: สมมติว่านักเรียนสองคนกำลังเล่นหมากรุกกัน ความน่าจะเป็นที่นักเรียน A ชนะในเกมที่กำหนดคือ 0.5 ความน่าจะเป็นที่นักเรียน B ชนะในเกมที่กำหนดคือ 0.3 และความน่าจะเป็นที่เสมอกันในเกมที่กำหนดคือ 0, 2 ถ้าพวกเขาเล่น 10 เกม จะเท่ากับเท่าใด ความน่าจะเป็นที่ผู้เล่น A ชนะ 4 ครั้ง ผู้เล่น B ชนะ 5 ครั้ง และเสมอกัน 1 ครั้ง?
คำตอบ: การใช้เครื่องคำนวณการกระจายพหุนามกับอินพุตต่อไปนี้ เราพบว่าความน่าจะเป็นคือ 0.038272:
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเบื้องต้นเกี่ยวกับการแจกแจงทั่วไปอื่นๆ ในสถิติ:
ความรู้เบื้องต้นเกี่ยวกับการแจกแจงแบบปกติ
ความรู้เบื้องต้นเกี่ยวกับการแจกแจงแบบทวินาม
ความรู้เบื้องต้นเกี่ยวกับการกระจายปัวซอง
ความรู้เบื้องต้นเกี่ยวกับการกระจายตัวทางเรขาคณิต