การกระจายส่วนเพิ่มคืออะไร?
ตารางความถี่แบบสองทาง คือตารางที่แสดงความถี่ (หรือ “จำนวน”) สำหรับตัวแปรประเภทสองตัว
ตัวอย่างเช่น ตารางสองทางต่อไปนี้แสดงผลการสำรวจที่ถามผู้คน 100 คนว่าพวกเขาชอบกีฬาประเภทใด: เบสบอล บาสเก็ตบอล หรือฟุตบอล
แถวแสดงเพศของผู้ตอบแบบสอบถาม และคอลัมน์ระบุกีฬาที่พวกเขาเลือก:

ในตัวอย่างนี้ มีตัวแปรสองตัว: กีฬาและเพศ
การแจกแจงส่วนเพิ่ม เป็นเพียงการแจกแจงของตัวแปรแต่ละตัวเหล่านี้ ในตารางแบบสองทาง การแจกแจงส่วนเพิ่มจะแสดงที่ ระยะขอบ ของตาราง:
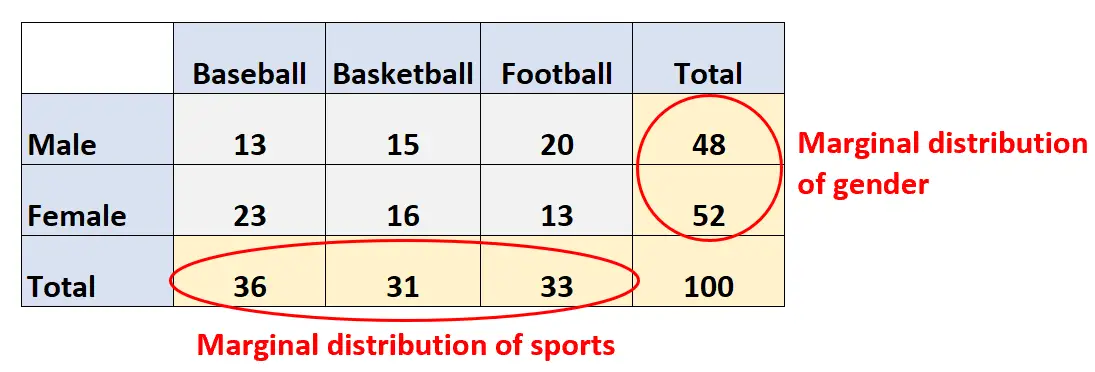
ตัวอย่างเช่น เราจะบอกว่าการกระจายส่วนเพิ่มของกีฬาคือ:
- เบสบอล: 36
- บาสเก็ตบอล: 31
- ฟุตบอล: 33
เรายังเขียนการกระจายส่วนเพิ่มของกีฬาเป็นเปอร์เซ็นต์ได้ (เช่น จากผู้ตอบแบบสอบถามทั้งหมด 100 คน):
- เบสบอล: 36/100 = 36%
- บาสเก็ตบอล: 31/100 = 31%
- ฟุตบอล: 33/100 = 33%
และเราจะบอกว่าการกระจายเพศชายขอบคือ:
- ชาย: 48 (หรือ 48%)
- หญิง: 52 (หรือ 52%)
หมายเหตุ: การแจกแจงส่วนเพิ่มจะรวมกันได้ 100% เสมอ
เหตุใดจึงใช้การแจกแจงส่วนเพิ่ม?
การแจกแจงส่วนเพิ่มมีประโยชน์เนื่องจากแม้ว่าเรามักจะรวบรวมข้อมูลสำหรับตัวแปรสองตัว (เช่น กีฬาและเพศ) แต่บางครั้งเราก็มีคำถามเฉพาะเจาะจงเกี่ยวกับตัวแปรเพียงตัวเดียว
ตัวอย่างเช่น เราอาจต้องการทราบการกระจายตัวของผู้ตอบแบบสำรวจตามเพศเท่านั้น
ในกรณีนี้ เราสามารถใช้การแจกแจงส่วนเพิ่มเพื่อค้นหาว่า 48% ของผู้ตอบแบบสอบถามเป็นชาย และ 52% ของผู้ตอบแบบสอบถามเป็นเพศหญิง
ใช้ตัวอย่างต่อไปนี้เป็นแนวทางปฏิบัติเพื่อทำความเข้าใจการแจกแจงส่วนเพิ่มให้ดียิ่งขึ้น
ตัวอย่างที่ 1: การแจกแจงส่วนเพิ่มสำหรับเปอร์เซ็นต์
ตารางสองทางต่อไปนี้นำเสนอผลการสำรวจที่ถามผู้คน 238 คนว่าพวกเขาชอบภาพยนตร์ประเภทใด:
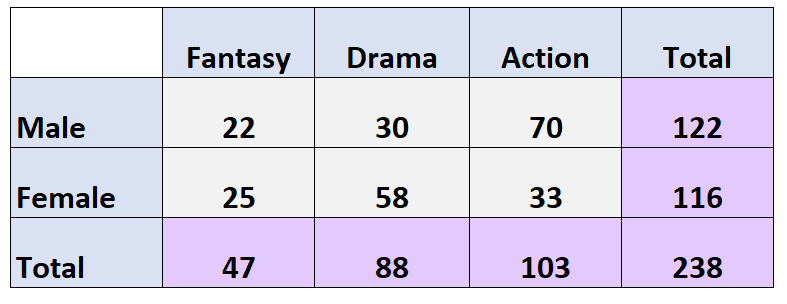
คำถาม: การกระจายส่วนเพิ่มตามประเภทภาพยนตร์เป็นเท่าใด (เป็นเปอร์เซ็นต์)
คำตอบ: การกระจายส่วนเพิ่มสำหรับประเภทภาพยนตร์มีดังนี้:
- แฟนตาซี: 47/238 = 19.7%
- ดราม่า: 88/238 = 37%
- การดำเนินการ: 103/238 = 43.3%
คำถาม: การกระจายเพศชายขอบ (เป็นเปอร์เซ็นต์) คืออะไร?
คำตอบ: การกระจายชายขอบตามเพศมีดังนี้:
- ผู้ชาย: 122/238 = 51.3%
- ผู้หญิง: 116/238 = 48.7%
ตัวอย่างที่ 2: การแจกแจงส่วนเพิ่มสำหรับบัญชี
ตารางสองทางต่อไปนี้แสดงคะแนนสอบของนักเรียน 64 คนในชั้นเรียนโดยพิจารณาจากจำนวนชั่วโมงที่พวกเขาใช้เวลาเรียน:
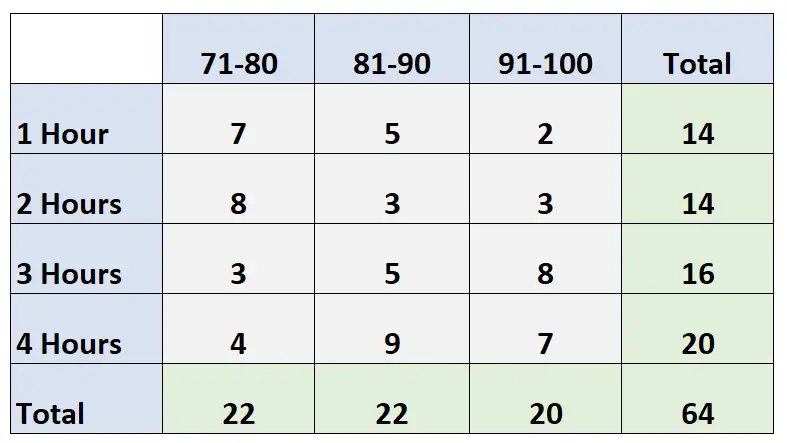
คำถาม: การกระจายคะแนนสอบแบบส่วนเพิ่ม (เป็นตัวเลข) คืออะไร?
คำตอบ: การกระจายคะแนนสอบส่วนเพิ่มคือ:
- 71-80: 22
- 81-90: 22
- 91-100: 20
คำถาม: การกระจายชั่วโมงการศึกษาส่วนเพิ่ม (เป็นตัวเลข) คืออะไร?
คำตอบ: การกระจายส่วนเพิ่มของชั่วโมงการศึกษาคือ:
- 1 ชั่วโมง: 14
- 2 ชั่วโมง: 14
- 3 ชั่วโมง: 16
- 4 ชั่วโมง: 20
โปรดทราบว่าผลรวมของการแจกแจงส่วนเพิ่มตรงกับผลรวมของตารางนักเรียน 64 คน
แหล่งข้อมูลเพิ่มเติม
สถิติเชิงพรรณนาหรือเชิงอนุมาน
ตัวแปรเชิงคุณภาพและเชิงปริมาณ
ระดับการวัด: ระบุ ลำดับ ช่วงเวลา และอัตราส่วน