การกระจายหมวดหมู่คืออะไร?
การแจกแจงแบบหมวดหมู่ คือการแจกแจงความน่าจะเป็นแบบแยกซึ่งอธิบายความน่าจะเป็น ที่ตัวแปรสุ่ม รับค่าที่เป็นของประเภทใดประเภทหนึ่ง K โดยที่แต่ละประเภทเชื่อมโยงกับความน่าจะเป็น
หากต้องการให้การแจกแจงจัดประเภทเป็นการแจกแจงตามหมวดหมู่ จะต้องเป็นไปตามเกณฑ์ต่อไปนี้:
- หมวดหมู่ไม่ต่อเนื่องกัน
- มีหมวดหมู่ที่เป็นไปได้สองหมวดหมู่ขึ้นไป
- ความน่าจะเป็นที่ตัวแปรสุ่มรับค่าในแต่ละหมวดหมู่จะต้องอยู่ระหว่าง 0 ถึง 1
- ผลรวมของความน่าจะเป็นสำหรับทุกหมวดหมู่จะต้องรวมกันได้ 1
ตัวอย่างที่ชัดเจนที่สุดของการกระจายตามหมวดหมู่คือการกระจายผลลัพธ์ที่เกี่ยวข้องกับการทอยลูกเต๋า มี K = 6 ผลลัพธ์ที่เป็นไปได้ และความน่าจะเป็นของแต่ละผลลัพธ์คือ 1/6:
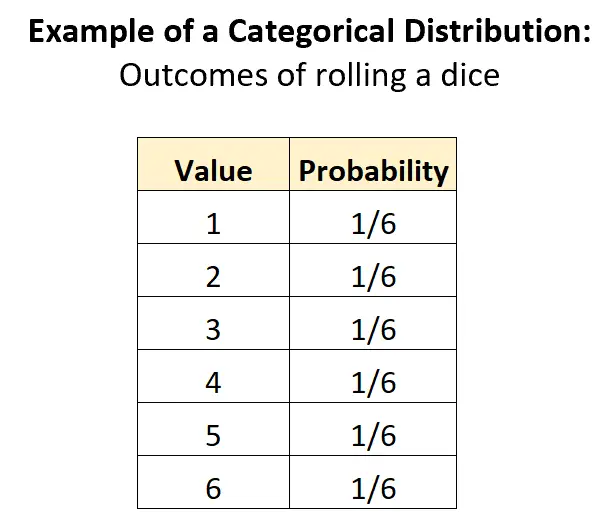
การแจกแจงนี้ตรงตามเกณฑ์ทั้งหมดที่จะจัดเป็นการแจกแจงตามหมวดหมู่:
- หมวดหมู่ไม่ต่อเนื่อง (เช่น ตัวแปรสุ่มสามารถรับเฉพาะค่าที่ไม่ต่อเนื่อง – 1, 2, 3, 4, 5, 6)
- มีหมวดหมู่ที่เป็นไปได้สองหมวดหมู่ขึ้นไป
- ความน่าจะเป็นของแต่ละหมวดหมู่อยู่ระหว่าง 0 ถึง 1
- ผลรวมของความน่าจะเป็นทั้งหมด 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1
กฎทั่วไป:
หากคุณสามารถ นับ จำนวนผลลัพธ์ได้ แสดงว่าคุณกำลังทำงานกับตัวแปรสุ่มแบบแยกส่วน เช่น การนับจำนวนครั้งที่เหรียญขึ้นหัว
แต่หากคุณสามารถ วัด ผลลัพธ์ได้ คุณกำลังทำงานกับตัวแปรสุ่มอย่างต่อเนื่อง เช่น การวัดส่วนสูง น้ำหนัก เวลา ฯลฯ
ตัวอย่างอื่น ๆ ของการแจกแจงตามหมวดหมู่
มีการแจกแจงตามหมวดหมู่มากมายในโลกแห่งความเป็นจริง ได้แก่:
ตัวอย่างที่ 1: พลิกเหรียญ
เมื่อเราทอยเหรียญ จะมีผลลัพธ์ที่เป็นไปได้ 2 แบบแยกกัน ความน่าจะเป็นของแต่ละผลลัพธ์จะอยู่ระหว่าง 0 ถึง 1 และผลรวมของความน่าจะเป็นเท่ากับ 1:
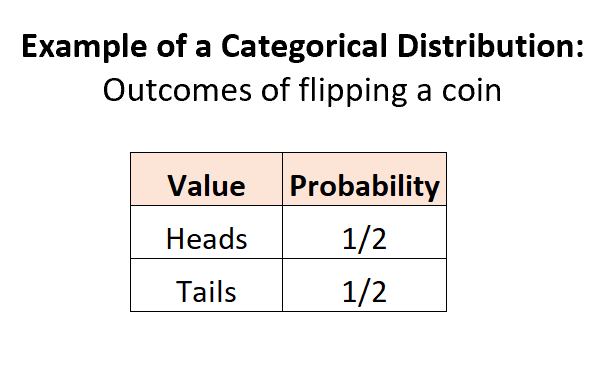
ตัวอย่างที่ 2: การเลือกหินอ่อนในโกศ
สมมติว่าโกศประกอบด้วยลูกหินสีแดง 5 ลูก ลูกหินสีเขียว 3 ลูก และลูกหินสีม่วง 2 ลูก หากเราสุ่มเลือกลูกบอลจากโกศ จะมีผลลัพธ์ที่เป็นไปได้ไม่ต่อเนื่องกัน 3 รายการ ความน่าจะเป็นของแต่ละผลลัพธ์จะอยู่ระหว่าง 0 ถึง 1 และผลรวมของความน่าจะเป็นเท่ากับ 1:
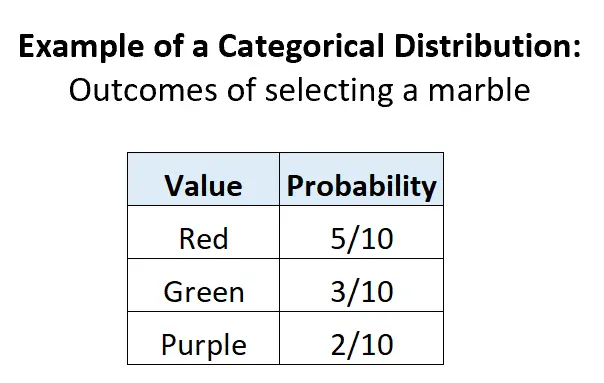
ตัวอย่างที่ 3: การเลือกไพ่จากสำรับ
หากเราสุ่มเลือกไพ่หนึ่งใบจากสำรับมาตรฐานจำนวน 52 ใบ จะมีผลลัพธ์ที่เป็นไปได้แบบไม่ต่อเนื่อง 13 แบบ ความน่าจะเป็นของแต่ละผลลัพธ์จะอยู่ระหว่าง 0 ถึง 1 และผลรวมของความน่าจะเป็นเท่ากับ 1:
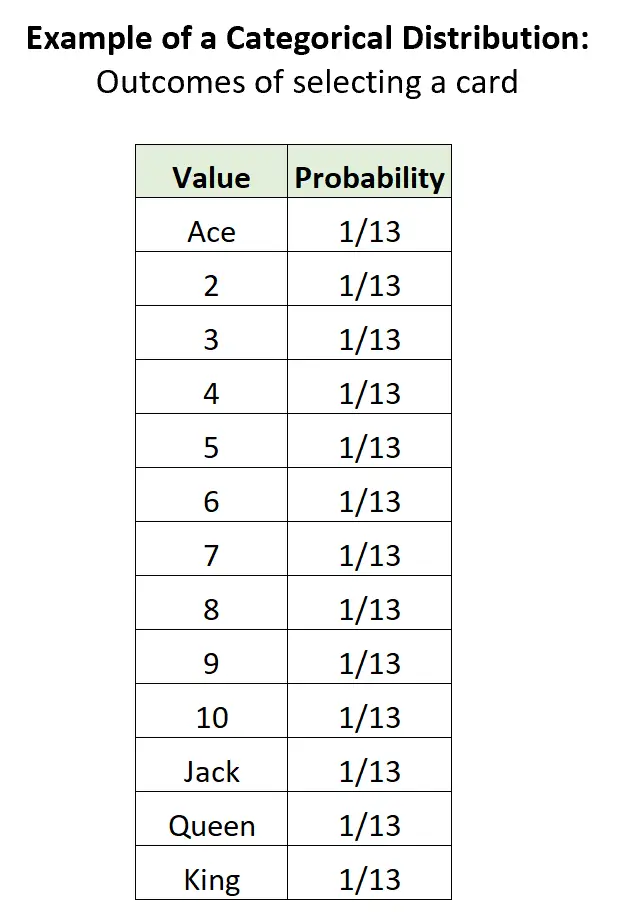
ความสัมพันธ์กับการแจกแจงอื่น
เพื่อให้การแจกแจงจำแนกเป็นการ แจกแจงแบบแบ่งหมวดหมู่ จะต้องมีผลลัพธ์ที่เป็นไปได้ K ≥ 2 และการทดลอง n = 1 ครั้ง
การใช้คำศัพท์นี้ การแจกแจงตามหมวดหมู่จะคล้ายกับการแจกแจงต่อไปนี้:
การแจกแจงเบอร์นูลลี: K = 2 ผลลัพธ์, n = 1 การทดสอบ
การแจกแจงทวินาม: K = 2 จุดสิ้นสุด, n ≥ 1 การทดลอง
การแจกแจงแบบพหุนาม: K ≥ 2 ผลลัพธ์, n ≥ การทดลอง
แหล่งข้อมูลเพิ่มเติม
ตัวแปรสุ่มคืออะไร?
ความรู้เบื้องต้นเกี่ยวกับการแจกแจงแบบทวินาม
ความรู้เบื้องต้นเกี่ยวกับการแจกแจงพหุนาม