การกระจายแบบเปิดคืออะไร?

ในสถิติ การแจกแจงแบบเปิด คือการแจกแจงความถี่ที่เปิดคลาส (หรือ “ถังขยะ”) อย่างน้อยหนึ่งคลาส

ตัวอย่างเช่น การแจกแจงความถี่ต่อไปนี้แสดงถึงการแจกแจงแบบเปิดซึ่งมีคลาสที่เล็กที่สุดเปิดอยู่:

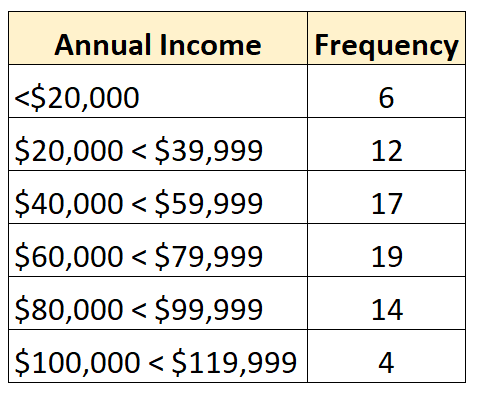
และการแจกแจงความถี่ต่อไปนี้แสดงการแจกแจงแบบเปิดซึ่งคลาสที่ใหญ่ที่สุดเปิดอยู่:

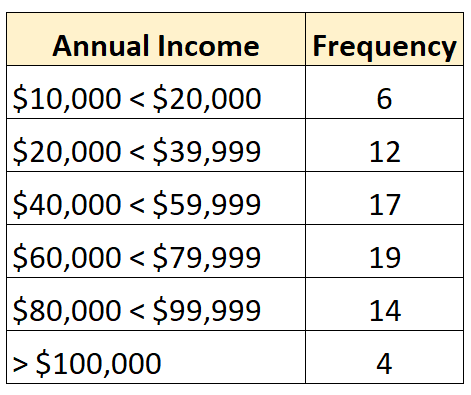
ในทางกลับกัน การแจกแจงแบบปิดคือการแจกแจงความถี่แต่ละคลาสมีขีดจำกัดบนและล่าง ดังตัวอย่างต่อไปนี้:

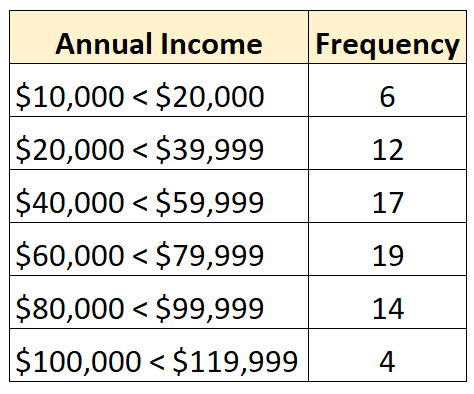
อะไรทำให้เกิดการแจกแจงแบบเปิด?

การแจกแจงแบบเปิดมักเป็นผลมาจากการที่นักวิจัยเลือกที่จะรวบรวมข้อมูลในลักษณะที่ทำให้คลาสใดคลาสหนึ่งกลายเป็นเปิด

ตัวอย่างเช่น สมมติว่านักวิจัยสำรวจผู้อยู่อาศัยในเมืองหนึ่งและถามพวกเขาเกี่ยวกับรายได้ต่อปีของครัวเรือน

ผู้วิจัยอาจเลือกที่จะให้คำตอบที่กว้างที่สุดที่เป็นไปได้คือ “>100,000 ดอลลาร์” เพราะพวกเขารู้ว่าผู้มีรายได้สูงอาจไม่สบายใจที่จะแบ่งปันรายได้ที่พวกเขาได้รับหากมากกว่า 100,000 ดอลลาร์อย่างมีนัยสำคัญ

ในทางกลับกัน ผู้วิจัยอาจเลือกที่จะให้คำตอบที่สั้นที่สุดเท่าที่จะเป็นไปได้ เพราะเขาหรือเธอรู้ดีว่าผู้อยู่อาศัยที่มีรายได้น้อยมากจะไม่สบายใจที่จะแบ่งปันสิ่งที่พวกเขามีรายได้น้อยเช่นกัน

โดยสรุป นักวิจัยมักจะรวมหลักสูตรแบบเปิดไว้ในแบบสำรวจ เนื่องจากพวกเขาต้องการเพิ่มจำนวนคนที่รู้สึกสบายใจที่จะตอบคำถามในการสำรวจให้มากที่สุด

ปัญหาเกี่ยวกับการแจกแจงแบบเปิด

ปัญหาของการแจกแจงแบบเปิดคือข้อมูลจริงถูก เซ็นเซอร์ กล่าวอีกนัยหนึ่ง เราสามารถทราบจำนวนผู้ที่มีรายได้มากกว่า 100,000 ดอลลาร์ในเมืองหนึ่งๆ แต่จริงๆ แล้ว เราไม่ทราบรายได้ต่อปีที่แน่นอนของพวกเขา

อาจเป็นไปได้ว่าบางคนมีรายได้ 150,000 ดอลลาร์ 250,000 ดอลลาร์ 500,000 ดอลลาร์ หรือมากกว่านั้น แต่เราไม่ทราบ เนื่องจากคนเหล่านี้แต่ละคนไม่สามารถระบุได้ว่าพวกเขามีรายได้ “>100,000 ดอลลาร์” ใน “การสอบสวน”

เนื่องจากข้อมูลถูกเซ็นเซอร์ในการแจกแจงแบบเปิด เราจึงไม่สามารถคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานที่แน่นอนของค่าในชุดข้อมูลได้ เนื่องจากเราไม่สามารถเข้าถึงค่าทั้งหมดในข้อมูลดิบได้

วิธีการวิเคราะห์การกระจายตัวแบบเปิด

เนื่องจากเราไม่สามารถคำนวณค่าเฉลี่ยที่แน่นอนของการแจกแจงแบบเปิดได้ เราจึงมักใช้ ค่ามัธยฐาน เป็นตัววัด “ศูนย์กลาง” ของชุดข้อมูล

โปรดจำไว้ว่าค่ามัธยฐานแสดงถึงค่ากลางของชุดข้อมูล

เมื่อทำงานกับการแจกแจงแบบเปิด เราสามารถใช้สูตรต่อไปนี้เพื่อค้นหาค่าประมาณค่ามัธยฐานที่ดีที่สุด:

ค่าประมาณมัธยฐานที่ดีที่สุด: L + ((n/2 – F) / f) * w

ทอง:

• L: ขีดจำกัดล่างของกลุ่มกลาง
• n: จำนวนการสังเกตทั้งหมด
• F: ความถี่สะสมจนถึงกลุ่มกลาง
• f: ความถี่ของกลุ่มกลาง
• w : ความกว้างของกลุ่มตรงกลาง

ตัวอย่างเช่น สมมติว่าเรามีการกระจายแบบเปิดดังต่อไปนี้:

ชุดข้อมูลจะมีทั้งหมด 72 ค่า ดังนั้นเราจึงรู้ว่า ค่ามัธยฐาน จะอยู่ระหว่างค่าที่ใหญ่ที่สุดลำดับที่ 36 ถึง 37 ในชุดข้อมูล แต่ละค่าเหล่านี้อยู่ในระดับ “60,000 – 79,999 เหรียญสหรัฐฯ” ดังนั้นเราจึงทราบว่ารายได้เฉลี่ยอยู่ในช่วงนั้น

ค่าประมาณมัธยฐานที่ดีที่สุดของเราคือ:

ค่ามัธยฐาน: 60,000 + ((72/2 – 25) / 19) * 19,999 = 71,578 ดอลลาร์

ค่านี้แสดงถึงค่าประมาณที่ดีที่สุดสำหรับรายได้เฉลี่ยต่อปีของบุคคลในชุดข้อมูลนี้