ปฏิบัติการบนฉาก: สหภาพ จุดตัด ส่วนเติมเต็ม และความแตกต่าง
เซต คือชุดขององค์ประกอบ
เรากำหนดชุดด้วยตัวพิมพ์ใหญ่ และกำหนดองค์ประกอบของชุดโดยใช้เครื่องหมายปีกกา ตัวอย่างเช่น สมมติว่าเรามีเซตชื่อ “A” ซึ่งมีสมาชิก 1, 2, 3 เราจะเขียนได้ดังนี้:
ก = {1, 2, 3}
บทช่วยสอนนี้จะอธิบาย การดำเนินการของชุด ที่ใช้บ่อยที่สุดในด้านความน่าจะเป็นและสถิติ
สหภาพแรงงาน
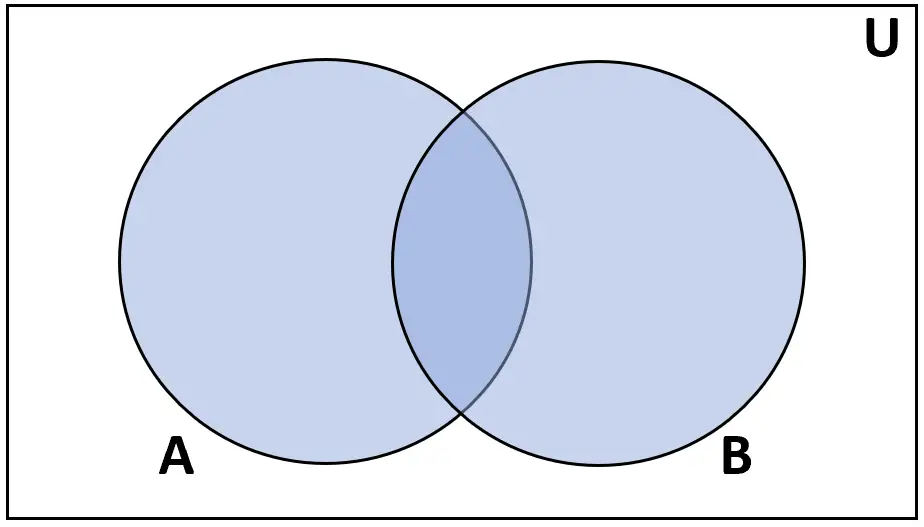
คำจำกัดความ: การรวมกัน ของเซต A และ B คือเซตขององค์ประกอบที่พบใน A หรือ B
เรตติ้ง: A ∪ B
ตัวอย่าง:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
จุดตัด
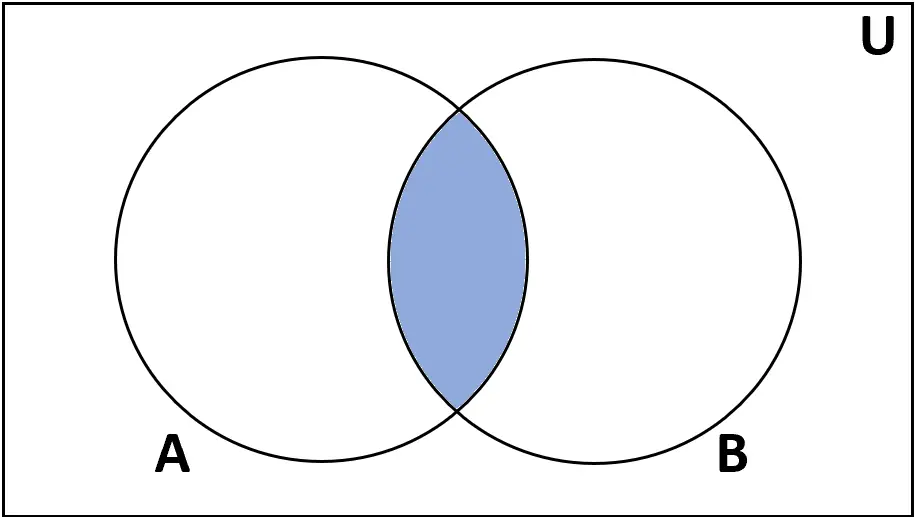
คำจำกัดความ: จุดตัด ของเซต A และ B คือเซตขององค์ประกอบที่พบในทั้ง A และ B
สัญกรณ์: A ∩ B
ตัวอย่าง:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
เสริม
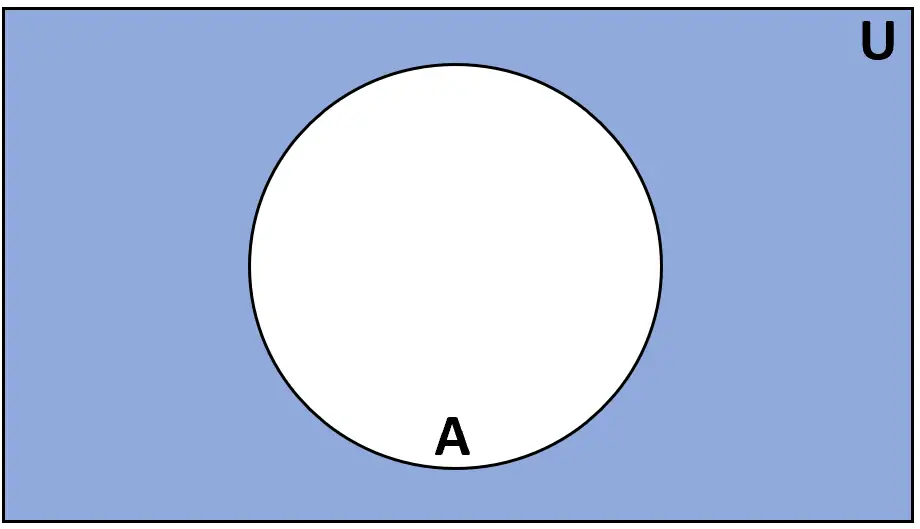
คำจำกัดความ: ส่วนเติมเต็ม ของเซต A คือเซตขององค์ประกอบที่อยู่ในเซต U สากลแต่ไม่อยู่ในเซต A
เรตติ้ง: A’ หรือ Ac
ตัวอย่าง:
- ถ้า U = {1, 2, 3, 4, 5, 6} และ A = {1, 2} แล้ว A c = {3, 4, 5, 6}
- ถ้า U = {1, 2, 3} และ A = {1, 2} แล้ว A c = {3}
ความแตกต่าง
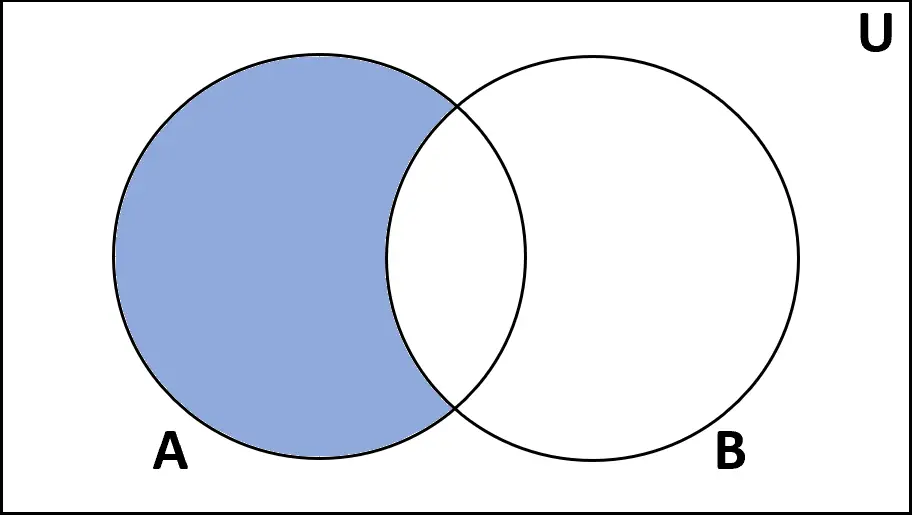
คำจำกัดความ: ความแตกต่าง ระหว่างเซต A และ B คือเซตขององค์ประกอบที่พบใน A แต่ไม่อยู่ในเซต B
การให้คะแนน: A-B
ตัวอย่าง:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
ความแตกต่างแบบสมมาตร
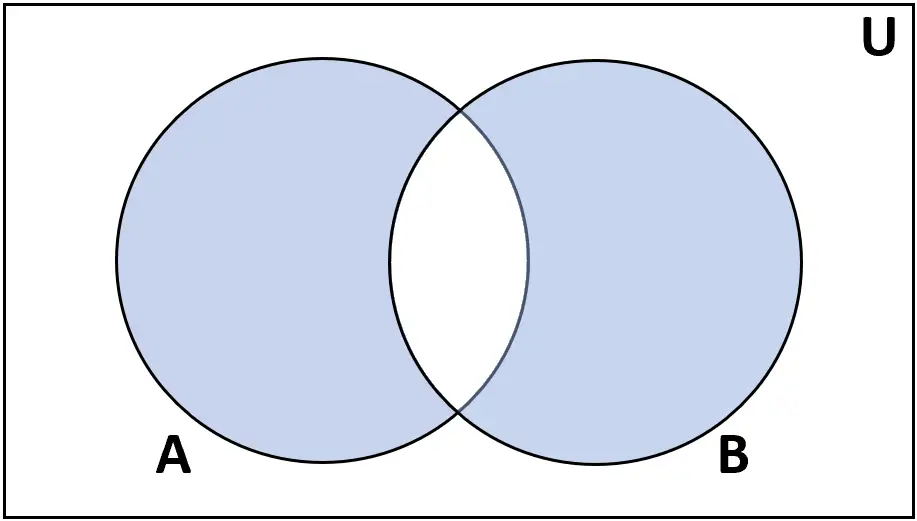
คำจำกัดความ: ผลต่างสมมาตร ของเซต A และ B คือเซตขององค์ประกอบที่พบใน A หรือ B แต่ไม่ใช่ทั้งสองอย่าง
เรตติ้ง: AΔB
ตัวอย่าง:
- {1, 2, 3} Δ {2, 3, 4} = {1, 4}
- {1, 2} Δ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
สินค้าคาร์ทีเซียน
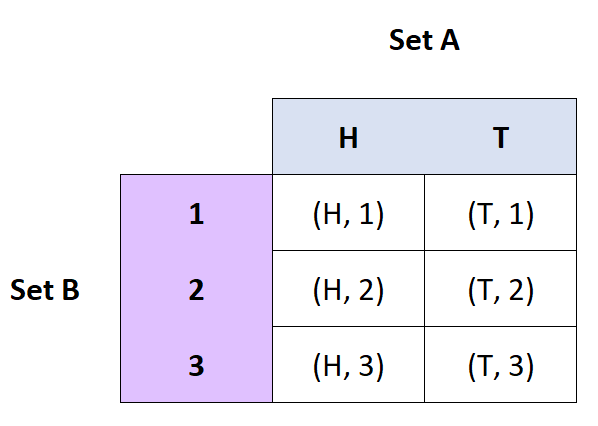
คำจำกัดความ: ผลคูณคาร์ทีเซียน ของเซต A และ B คือเซตของคู่อันดับของ A และ B
เรตติ้ง: A x B
ตัวอย่าง:
- ถ้า A = {H, T} และ B = {1, 2, 3} แล้ว A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( ต, 2), (ต, 3)}
- ถ้า A = {T, H} และ B = {1, 2, 3} แล้ว A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( ฮ, 2), (เอช, 3)}