วิธีดำเนินการถดถอยกำลังสองใน r
เมื่อตัวแปรสองตัวมีความสัมพันธ์เชิงเส้น เรามักจะใช้ การถดถอยเชิงเส้นอย่างง่าย เพื่อหาปริมาณความสัมพันธ์ของตัวแปรทั้งสอง

อย่างไรก็ตาม เมื่อตัวแปรสองตัวมีความสัมพันธ์แบบกำลังสอง เราสามารถใช้ การถดถอยกำลังสอง เพื่อหาปริมาณความสัมพันธ์ของตัวแปรทั้งสองได้

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยกำลังสองใน R
ตัวอย่าง: การถดถอยกำลังสองใน R
สมมติว่าเราต้องการเข้าใจความสัมพันธ์ระหว่างจำนวนชั่วโมงทำงานกับความสุขที่รายงาน เรามีข้อมูลเกี่ยวกับจำนวนชั่วโมงทำงานต่อสัปดาห์และรายงานระดับความสุข (ในระดับ 0 ถึง 100) สำหรับคน 11 คนดังต่อไปนี้:

ใช้ขั้นตอนต่อไปนี้เพื่อให้พอดีกับแบบจำลองการถดถอยกำลังสองใน R
ขั้นตอนที่ 1: ป้อนข้อมูล
ขั้นแรก เราจะสร้าง data frame ที่มีข้อมูลของเรา:
#createdata data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60), happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27)) #viewdata data hours happiness 1 6 14 2 9 28 3 12 50 4 14 70 5 30 89 6 35 94 7 40 90 8 47 75 9 51 59 10 55 44 11 60 27
ขั้นตอนที่ 2: แสดงภาพข้อมูล
ต่อไป เราจะสร้าง Scatterplot แบบง่ายเพื่อแสดงข้อมูลเป็นภาพ
#create scatterplot
plot(data$hours, data$happiness, pch=16)
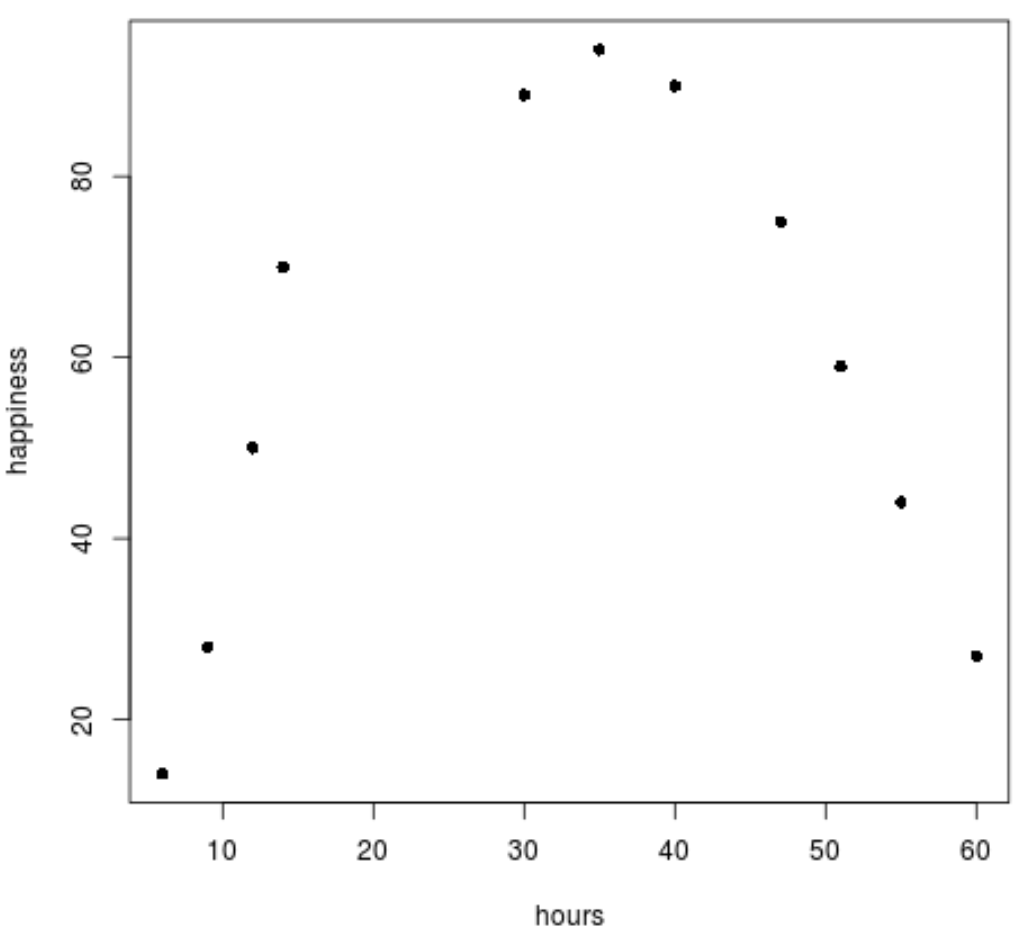
เราจะเห็นได้อย่างชัดเจนว่าข้อมูลไม่เป็นไปตามรูปแบบเชิงเส้น
ขั้นตอนที่ 3: ติดตั้งโมเดลการถดถอยเชิงเส้นอย่างง่าย
ต่อไป เราจะใส่โมเดลการถดถอยเชิงเส้นอย่างง่ายเพื่อดูว่าโมเดลนี้เข้ากับข้อมูลได้ดีเพียงใด:
#fit linear model linearModel <- lm(happiness ~ hours, data=data) #view model summary summary(linearModel) Call: lm(formula = happiness ~ hours) Residuals: Min 1Q Median 3Q Max -39.34 -21.99 -2.03 23.50 35.11 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 48.4531 17.3288 2.796 0.0208 * hours 0.2981 0.4599 0.648 0.5331 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 28.72 on 9 degrees of freedom Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331
ความแปรปรวนรวมของความสุขที่อธิบายโดยแบบจำลองคือเพียง 4.46% ดังที่แสดงด้วยค่า R-squared หลายค่า
ขั้นตอนที่ 4: ติดตั้งแบบจำลองการถดถอยกำลังสอง
ต่อไป เราจะใส่แบบจำลองการถดถอยกำลังสองพอดี
#create a new variable for hours 2 data$hours2 <- data$hours^2 #fit quadratic regression model quadraticModel <- lm(happiness ~ hours + hours2, data=data) #view model summary summary(quadraticModel) Call: lm(formula = happiness ~ hours + hours2, data = data) Residuals: Min 1Q Median 3Q Max -6.2484 -3.7429 -0.1812 1.1464 13.6678 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -18.25364 6.18507 -2.951 0.0184 * hours 6.74436 0.48551 13.891 6.98e-07 *** hours2 -0.10120 0.00746 -13.565 8.38e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 6.218 on 8 degrees of freedom Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06
ความแปรปรวนรวมของความสุขที่อธิบายโดยแบบจำลองเพิ่มขึ้นเป็น 96.02%
เราสามารถใช้โค้ดต่อไปนี้เพื่อดูว่าแบบจำลองเหมาะสมกับข้อมูลได้ดีเพียงใด:
#create sequence of hour values hourValues <- seq(0, 60, 0.1) #create list of predicted happiness levels using quadratic model happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2)) #create scatterplot of original data values plot(data$hours, data$happiness, pch=16) #add predicted lines based on quadratic regression model lines(hourValues, happinessPredict, col='blue')
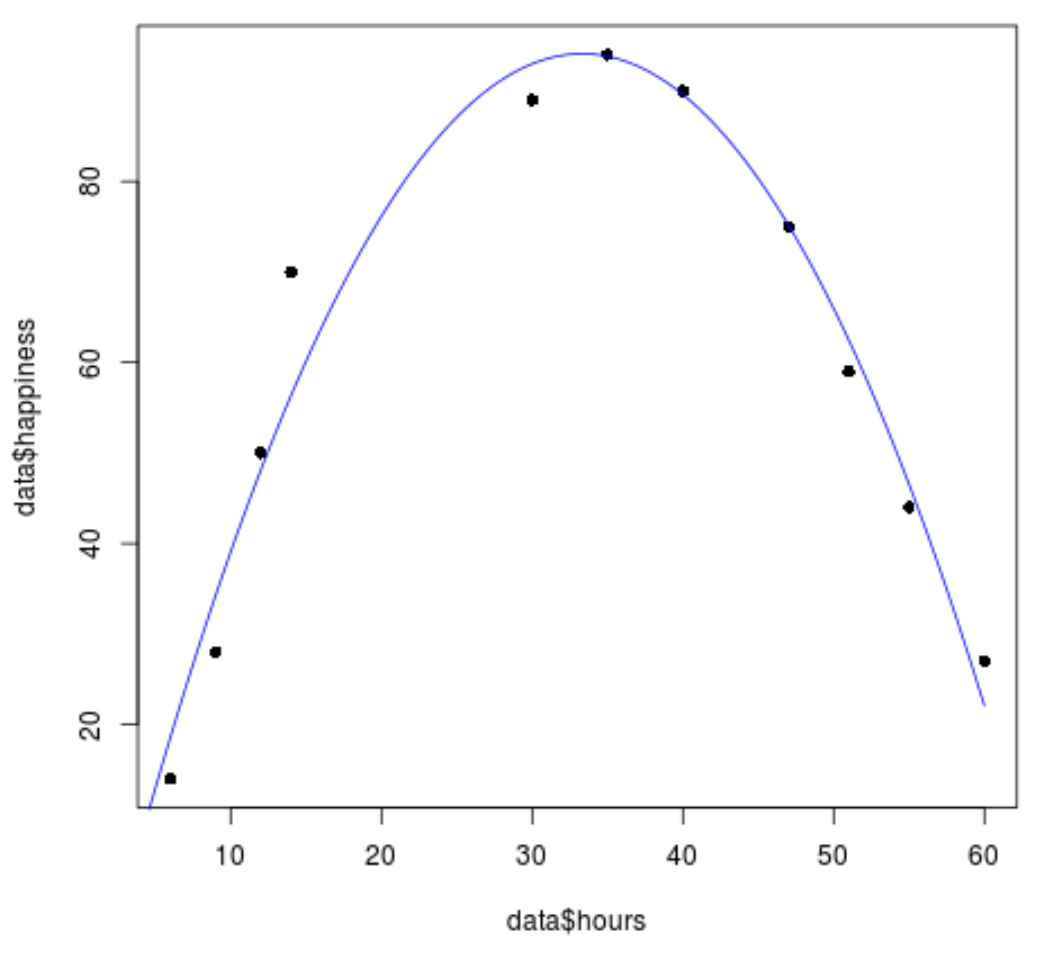
เราจะเห็นได้ว่าเส้นถดถอยกำลังสองเหมาะสมกับค่าข้อมูลค่อนข้างดี
ขั้นตอนที่ 5: ตีความแบบจำลองการถดถอยกำลังสอง
ในขั้นตอนที่แล้ว เราพบว่าผลลัพธ์ของแบบจำลองการถดถอยกำลังสองคือ:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -18.25364 6.18507 -2.951 0.0184 *
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
จากค่าสัมประสิทธิ์ที่นำเสนอในที่นี้ การถดถอยกำลังสองที่ปรับแล้วจะเป็น:
ความสุข = -0.1012 (ชั่วโมง) 2 + 6.7444 (ชั่วโมง) – 18.2536
เราสามารถใช้สมการนี้เพื่อค้นหาความสุขที่คาดการณ์ไว้ของแต่ละคน โดยพิจารณาจากจำนวนชั่วโมงทำงานต่อสัปดาห์
เช่น คนที่ทำงาน 60 ชั่วโมงต่อสัปดาห์ จะมีระดับความสุขเท่ากับ 22.09 :
ความสุข = -0.1012(60) 2 + 6.7444(60) – 18.2536 = 22.09
ในทางกลับกัน คนที่ทำงาน 30 ชั่วโมงต่อสัปดาห์ควรมีระดับความสุขอยู่ที่ 92.99 :
ความสุข = -0.1012(30) 2 + 6.7444(30) – 18.2536 = 92.99