วิธีการทำการถดถอยเชิงเส้นอย่างง่ายใน python (ทีละขั้นตอน)

การถดถอยเชิงเส้นอย่างง่าย เป็นเทคนิคที่เราสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่าง ตัวแปรอธิบาย ตัวเดียวและ ตัวแปรตอบสนอง ตัวเดียว

เทคนิคนี้ค้นหาบรรทัดที่ “เหมาะสม” กับข้อมูลมากที่สุดและใช้รูปแบบต่อไปนี้:

ŷ = ข ₀ + ข ₁ x

ทอง:

• ŷ : ค่าตอบกลับโดยประมาณ
• b ₀ : ต้นกำเนิดของเส้นถดถอย
• b ₁ : ความชันของเส้นถดถอย

สมการนี้สามารถช่วยให้เราเข้าใจความสัมพันธ์ระหว่างตัวแปรอธิบายและตัวแปรตอบสนอง และ (สมมติว่ามีนัยสำคัญทางสถิติ) สามารถใช้เพื่อทำนายค่าของตัวแปรตอบสนองโดยพิจารณาจากค่าของตัวแปรอธิบายได้

บทช่วยสอนนี้ให้คำอธิบายทีละขั้นตอนเกี่ยวกับวิธีการถดถอยเชิงเส้นอย่างง่ายใน Python

ขั้นตอนที่ 1: โหลดข้อมูล

สำหรับตัวอย่างนี้ เราจะสร้างชุดข้อมูลปลอมที่มีตัวแปรสองตัวต่อไปนี้สำหรับนักเรียน 15 คน:

• จำนวนชั่วโมงเรียนทั้งหมดสำหรับการสอบบางประเภท
• ผลสอบ

เราจะพยายามปรับโมเดลการถดถอยเชิงเส้นอย่างง่ายโดยใช้ ชั่วโมง เป็นตัวแปรอธิบายและ ผลการทดสอบ เป็นตัวแปรตอบสนอง

รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลปลอมใน Python:

 import pandas as pd

#create dataset
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})
      

#view first six rows of dataset
df[0:6]

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81

ขั้นตอนที่ 2: แสดงภาพข้อมูล

ก่อนที่จะปรับโมเดลการถดถอยเชิงเส้นอย่างง่าย เราต้องแสดงภาพข้อมูลก่อนจึงจะเข้าใจได้

อันดับแรก เราต้องการให้แน่ใจว่าความสัมพันธ์ระหว่าง ชั่วโมง และ คะแนน เป็นเส้นตรงโดยประมาณ เนื่องจากนี่เป็น สมมติฐานพื้นฐาน ของการถดถอยเชิงเส้นอย่างง่าย

เราสามารถสร้าง Scatterplot ง่ายๆ เพื่อให้เห็นภาพความสัมพันธ์ระหว่างตัวแปรทั้งสอง:

 import matplotlib.pyplot as plt

plt. scatter (df.hours, df.score)
plt. title (' Hours studied vs. Exam Score ')
plt. xlabel (' Hours ')
plt. ylabel (' Score ')
plt. show ()

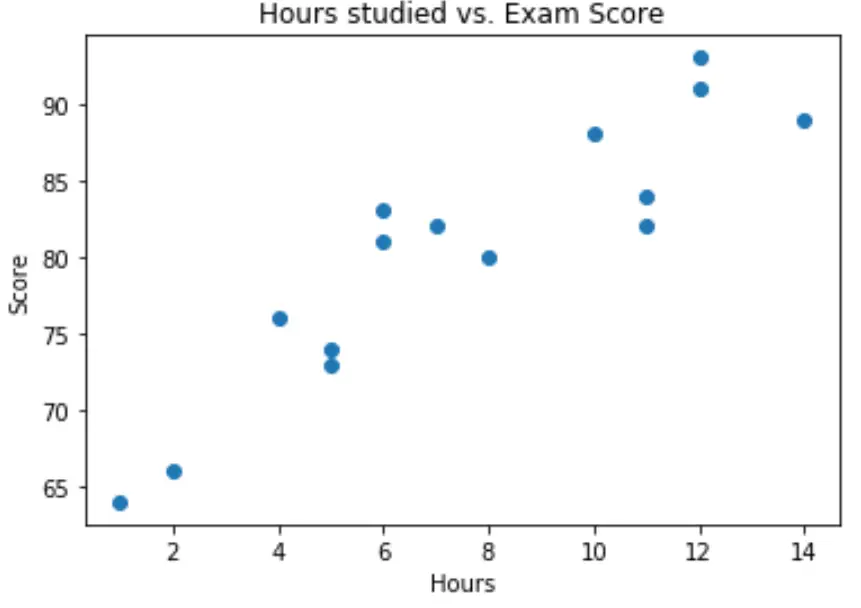
จากกราฟเราจะเห็นว่าความสัมพันธ์มีลักษณะเป็นเส้นตรง เมื่อ จำนวนชั่วโมง เพิ่มขึ้น คะแนน ก็มีแนวโน้มที่จะเพิ่มขึ้นเป็นเส้นตรงเช่นกัน

จากนั้นเราสามารถสร้าง boxplot เพื่อให้เห็นภาพการกระจายผลการสอบและตรวจสอบ ค่าผิดปกติ ตามค่าเริ่มต้น Python จะกำหนดการสังเกตเป็นค่าผิดปกติหากเป็น 1.5 เท่าของช่วงระหว่างควอไทล์ที่อยู่เหนือควอไทล์ที่ 3 (Q3) หรือ 1.5 เท่าของช่วงระหว่างควอไทล์ที่ต่ำกว่าควอร์ไทล์ที่ 1 (Q1)

หากการสังเกตนั้นผิดปกติ วงกลมเล็กๆ จะปรากฏขึ้นใน boxplot:

 df. boxplot (column=[' score ']) 

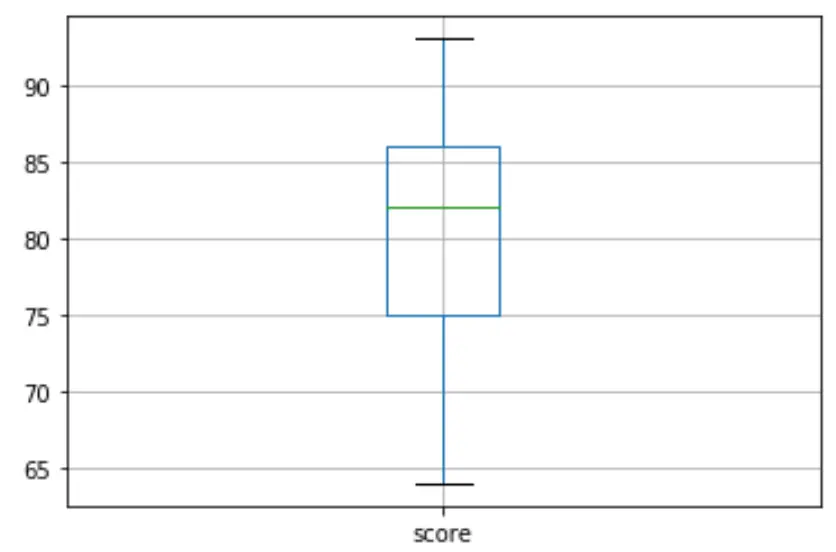
ไม่มีวงกลมเล็กๆ ใน boxplot ซึ่งหมายความว่าไม่มีค่าผิดปกติในชุดข้อมูลของเรา

ขั้นตอนที่ 3: ทำการถดถอยเชิงเส้นอย่างง่าย

เมื่อเราได้รับการยืนยันแล้วว่าความสัมพันธ์ระหว่างตัวแปรของเราเป็นแบบเส้นตรงและไม่มีค่าผิดปกติ เราสามารถดำเนินการสร้างแบบจำลองการถดถอยเชิงเส้นอย่างง่ายโดยใช้ ชั่วโมง เป็นตัวแปรอธิบาย และ ใช้คะแนน เป็นตัวแปรตอบสนอง:

หมายเหตุ: เราจะใช้ ฟังก์ชัน OLS() จากไลบรารี statsmodels เพื่อให้พอดีกับโมเดลการถดถอย

 import statsmodels.api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06
Time: 15:51:45 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

จากสรุปแบบจำลอง เราจะเห็นว่าสมการถดถอยที่ติดตั้งคือ:

คะแนน = 65.334 + 1.9824*(ชั่วโมง)

ซึ่งหมายความว่าแต่ละชั่วโมงที่เรียนเพิ่มเติมจะสัมพันธ์กับคะแนนสอบเฉลี่ยที่เพิ่มขึ้น 1.9824 คะแนน และค่าเดิมที่ 65,334 บอกเราถึงคะแนนสอบเฉลี่ยที่คาดหวังสำหรับนักเรียนที่เรียนเป็นเวลา 0 ชั่วโมง

นอกจากนี้เรายังสามารถใช้สมการนี้เพื่อค้นหาคะแนนสอบที่คาดหวังโดยพิจารณาจากจำนวนชั่วโมงที่นักเรียนเรียน เช่น นักเรียนที่เรียน 10 ชั่วโมง ควรได้คะแนนสอบ 85.158 :

คะแนน = 65.334 + 1.9824*(10) = 85.158

ต่อไปนี้เป็นวิธีการตีความสรุปแบบจำลองที่เหลือ:

• ป>|t| : นี่คือค่า p ที่เกี่ยวข้องกับค่าสัมประสิทธิ์แบบจำลอง เนื่องจากค่า p สำหรับ ชั่วโมง (0.000) น้อยกว่า 0.05 อย่างมีนัยสำคัญ เราจึงสามารถพูดได้ว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่าง ชั่วโมง และ คะแนน
• R-squared: ตัวเลขนี้บอกเราว่าเปอร์เซ็นต์ของความแปรผันของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่เรียน โดยทั่วไป ยิ่งค่า R-squared ของแบบจำลองการถดถอยมีค่ามากเท่าใด ตัวแปรอธิบายก็จะสามารถทำนายค่าของตัวแปรตอบสนองได้ดีขึ้นเท่านั้น ในกรณีนี้ 83.1% ของความแปรผันของคะแนนอธิบายเป็นชั่วโมงที่ศึกษา
• สถิติ F และค่า p: สถิติ F ( 63.91 ) และค่า p ที่สอดคล้องกัน ( 2.25e-06 ) บอกเราถึงความสำคัญโดยรวมของแบบจำลองการถดถอย กล่าวคือ ตัวแปรอธิบายในแบบจำลองมีประโยชน์ในการอธิบายการเปลี่ยนแปลงหรือไม่ . ในตัวแปรตอบสนอง เนื่องจากค่า p ในตัวอย่างนี้น้อยกว่า 0.05 แบบจำลองของเราจึงมีนัยสำคัญทางสถิติ และ ชั่วโมง จึงถือว่ามีประโยชน์ในการอธิบายความแปรผันของ คะแนน

ขั้นตอนที่ 4: สร้างแปลงที่เหลือ

หลังจากปรับแบบจำลองการถดถอยเชิงเส้นอย่างง่ายเข้ากับข้อมูลแล้ว ขั้นตอนสุดท้ายคือการสร้างแปลงส่วนที่เหลือ

ข้อสันนิษฐานสำคัญประการหนึ่งของการถดถอยเชิงเส้นคือส่วนที่เหลือของแบบจำลองการถดถอยจะมีการกระจายตามปกติโดยประมาณและเป็น โฮโมสซิดาสติก ในแต่ละระดับของตัวแปรอธิบาย หากไม่เป็นไปตามสมมติฐานเหล่านี้ ผลลัพธ์ของแบบจำลองการถดถอยของเราอาจทำให้เข้าใจผิดหรือไม่น่าเชื่อถือ

เพื่อตรวจสอบว่าเป็นไปตามสมมติฐานเหล่านี้ เราสามารถสร้างแปลงที่เหลือต่อไปนี้:

แผนภาพค่าคงเหลือเทียบกับค่าที่พอดี: แผนภาพนี้มีประโยชน์สำหรับการยืนยันความเป็นเนื้อเดียวกัน แกน x จะแสดงค่าที่พอดี และแกน y จะแสดงค่าคงเหลือ ตราบใดที่ส่วนที่เหลือปรากฏว่ามีการกระจายแบบสุ่มและสม่ำเสมอทั่วทั้งกราฟรอบๆ ค่าศูนย์ เราสามารถสรุปได้ว่าความเป็นเนื้อเดียวกันจะไม่ถูกละเมิด:

 #define figure size
fig = plt. figure (figsize=(12.8))

#produce residual plots
fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)

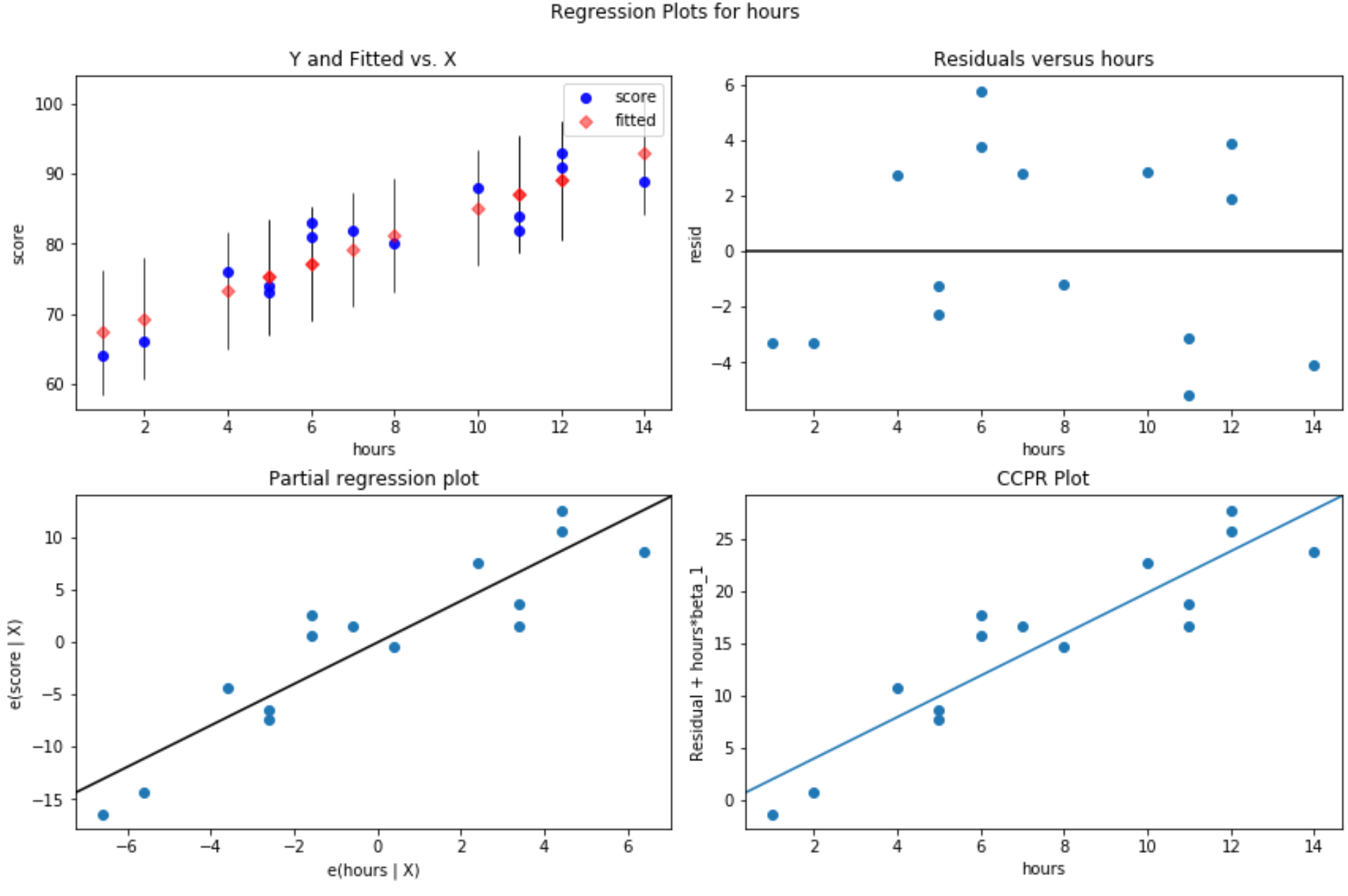
มีการผลิตสี่แปลง อันที่มุมขวาบนคือพล็อตที่เหลือเทียบกับพล็อตที่ปรับแล้ว แกน x บนพล็อตนี้แสดงค่าที่แท้จริงของ จุด ตัวแปรทำนายและแกน y จะแสดงค่าคงเหลือสำหรับค่านั้น

เนื่องจากสิ่งตกค้างดูเหมือนจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์ นี่บ่งชี้ว่าความต่างกันไม่เป็นปัญหากับตัวแปรอธิบาย

พล็อต QQ: พล็อตนี้มีประโยชน์ในการพิจารณาว่าส่วนที่เหลือเป็นไปตามการแจกแจงแบบปกติหรือไม่ หากค่าข้อมูลในพล็อตเป็นเส้นตรงประมาณ 45 องศา แสดงว่าข้อมูลมีการกระจายตามปกติ:

 #define residuals
res = model. reside

#create QQ plot
fig = sm. qqplot (res, fit= True , line=" 45 ")
plt.show() 

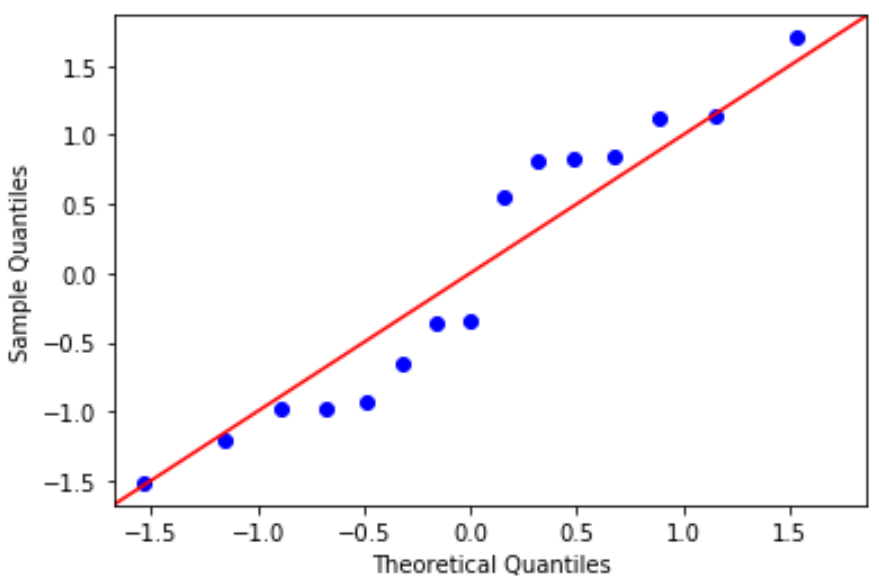
สารตกค้างเบี่ยงเบนไปจากเส้น 45 องศาเล็กน้อย แต่ไม่มากพอที่จะทำให้เกิดความกังวลร้ายแรง เราสามารถสรุปได้ว่าเป็นไปตามสมมติฐานปกติ

เนื่องจากส่วนที่เหลือมีการกระจายตามปกติและเป็นโฮโมสซิดาสติก เราจึงตรวจสอบได้ว่าเป็นไปตามสมมติฐานของแบบจำลองการถดถอยเชิงเส้นอย่างง่าย ดังนั้นผลลัพธ์ของแบบจำลองของเราจึงมีความน่าเชื่อถือ

รหัส Python แบบเต็มที่ใช้ในบทช่วยสอนนี้สามารถพบได้ ที่นี่