วิธีดำเนินการทดสอบ log rank ใน r

การทดสอบอันดับบันทึก เป็นวิธีที่ใช้กันทั่วไปในการเปรียบเทียบเส้นโค้งการอยู่รอดระหว่างสองกลุ่ม

การทดสอบนี้ใช้ สมมติฐาน ดังต่อไปนี้:

H ₀ : ไม่มีความแตกต่างในการอยู่รอดระหว่างทั้งสองกลุ่ม

_HA : มี ความแตกต่างในการเอาชีวิตรอดระหว่างทั้งสองกลุ่ม

หาก ค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด (เช่น α = 0.05) เราก็สามารถปฏิเสธสมมติฐานที่เป็นโมฆะได้และสรุปว่ามีหลักฐานเพียงพอที่จะบอกว่ามีความแตกต่างในการอยู่รอดระหว่างทั้งสองกลุ่ม

หากต้องการทำการทดสอบระดับบันทึกใน R เราสามารถใช้ฟังก์ชัน survdiff() จากแพ็คเกจ survival ซึ่งใช้ไวยากรณ์ต่อไปนี้:

Survdiff(ความอยู่รอด(เวลา, สถานะ) ~ ตัวทำนาย, ข้อมูล)

ฟังก์ชันนี้จะส่งคืนสถิติการทดสอบไคสแควร์และค่า p ที่สอดคล้องกัน

ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้เพื่อทำการทดสอบระดับบันทึกใน R

ตัวอย่าง: การทดสอบอันดับบันทึกใน R

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล รังไข่ จากแพ็คเกจ การอยู่รอด ชุดข้อมูลนี้ประกอบด้วยข้อมูลต่อไปนี้เกี่ยวกับผู้ป่วย 26 ราย:

• ระยะเวลารอดชีวิต (เป็นเดือน) หลังจากได้รับการวินิจฉัยว่าเป็นมะเร็งรังไข่
• มีการเซ็นเซอร์เวลาเอาชีวิตรอดหรือไม่
• ประเภทการรักษาที่ได้รับ (rx = 1 หรือ rx = 2)

รหัสต่อไปนี้แสดงวิธีการแสดงหกแถวแรกของชุดข้อมูลนี้:

 library (survival)

#view first six rows of dataset
head(ovarian)

  futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5,431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2

รหัสต่อไปนี้แสดงวิธีดำเนินการทดสอบระดับบันทึกเพื่อตรวจสอบว่ามีความแตกต่างในการรอดชีวิตระหว่างผู้ป่วยที่ได้รับการรักษาที่แตกต่างกันหรือไม่:

 #perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06

 Chisq= 1.1 on 1 degrees of freedom, p= 0.3 

สถิติการทดสอบไคสแควร์คือ 1.1 โดยมีระดับความอิสระ 1 องศา และค่า p ที่สอดคล้องกันคือ 0.3 เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้

กล่าวอีกนัยหนึ่ง เราไม่มีหลักฐานเพียงพอที่จะกล่าวว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในการรอดชีวิตระหว่างการรักษาทั้งสอง

นอกจากนี้เรายังสามารถวาดเส้นโค้งการเอาชีวิตรอดสำหรับแต่ละกลุ่มได้โดยใช้ไวยากรณ์ต่อไปนี้:

 #plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), 
     xlab = " Time ", 
     ylab = “ Overall survival probability ”)

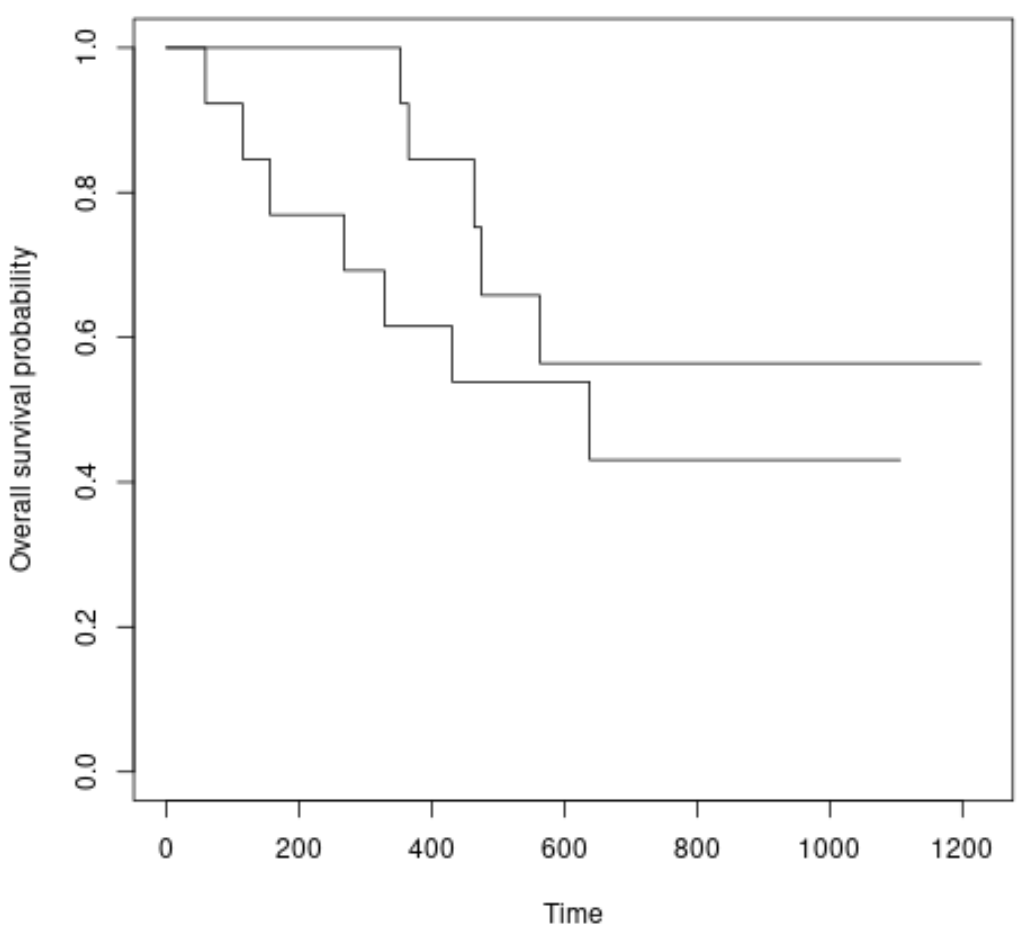
เราจะเห็นว่าเส้นโค้งการเอาชีวิตรอดแตกต่างกันเล็กน้อย แต่การทดสอบระดับบันทึกบอกเราว่าความแตกต่างนั้นไม่มีนัยสำคัญทางสถิติ