การทดสอบ augmented dickey-fuller ใน r (พร้อมตัวอย่าง)
อนุกรมเวลาจะเรียกว่า “คงที่” หากไม่มีแนวโน้ม นำเสนอความแปรปรวนคงที่ตลอดเวลา และมีโครงสร้างความสัมพันธ์อัตโนมัติที่คงที่ตลอดเวลา
วิธีหนึ่งในการทดสอบว่าอนุกรมเวลาคงที่หรือไม่คือทำการ ทดสอบ Augmented Dickey–Fuller ซึ่งใช้สมมติฐานว่างและสมมติฐานทางเลือกต่อไปนี้:
H 0 : อนุกรมเวลาไม่คงที่ กล่าวอีกนัยหนึ่ง โครงสร้างของมันขึ้นอยู่กับเวลา และการแปรผันของมันไม่คงที่เมื่อเวลาผ่านไป
H A : อนุกรมเวลาหยุดนิ่ง
ถ้า ค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด (เช่น α = 0.05) เราก็สามารถปฏิเสธสมมติฐานที่เป็นโมฆะและสรุปได้ว่าอนุกรมเวลาเป็นแบบคงที่
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีดำเนินการทดสอบ Augmented Dickey-Fuller ใน R สำหรับอนุกรมเวลาที่กำหนด
ตัวอย่าง: การทดสอบ Augmented Dickey-Fuller ใน R
สมมติว่าเรามีข้อมูลอนุกรมเวลาต่อไปนี้ใน R:
data <- c(3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10)
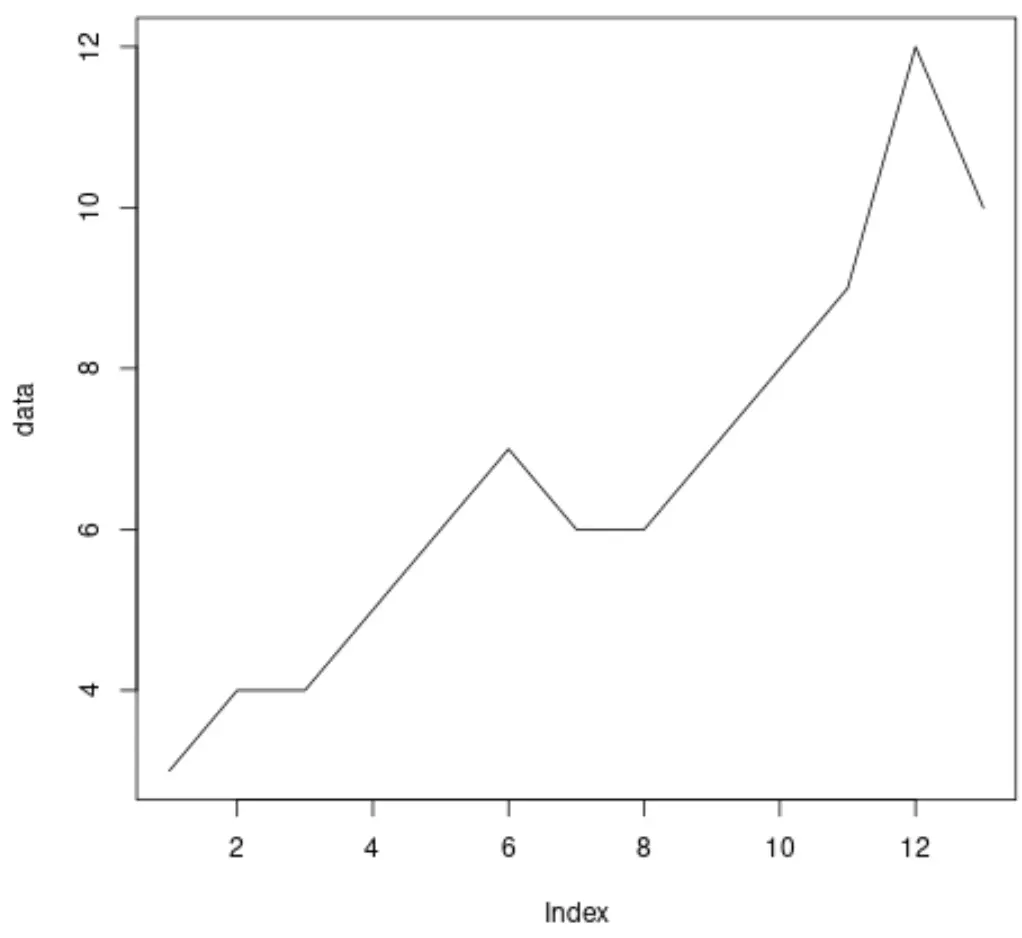
ก่อนที่จะทำการทดสอบ Augmented Dickey-Fuller กับข้อมูล เราสามารถสร้างพล็อตด่วนเพื่อแสดงภาพข้อมูลได้:
plot(data, type=' l ')
ในการทำการทดสอบ Augmented Dickey-Fuller เราสามารถใช้ฟังก์ชัน adf.test() จากไลบรารี tseries
รหัสต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้:
library (tseries) #perform augmented Dickey-Fuller test adf.test(data) Augmented Dickey-Fuller Test data:data Dickey-Fuller = -2.2048, Lag order = 2, p-value = 0.4943 alternative hypothesis: stationary
ต่อไปนี้เป็นวิธีตีความค่าที่สำคัญที่สุดของผลลัพธ์:
- สถิติการทดสอบ: -2.2048
- ค่า P: 0.4943
เนื่องจากค่า p ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้
ซึ่งหมายความว่าอนุกรมเวลาไม่คงที่ กล่าวอีกนัยหนึ่ง โครงสร้างของมันขึ้นอยู่กับเวลา และการแปรผันของมันไม่คงที่เมื่อเวลาผ่านไป
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:
วิธีการทดสอบแนวโน้ม Mann-Kendall ใน R
วิธีการพล็อตอนุกรมเวลาใน R
วิธีลดแนวโน้มข้อมูล