วิธีดำเนินการทดสอบ f บางส่วนใน excel
การทดสอบ F บางส่วน ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่าง แบบจำลองการถดถอย และเวอร์ชันที่ซ้อนกันของแบบจำลองเดียวกันหรือไม่
โมเดล แบบซ้อน เป็นเพียงโมเดลที่ประกอบด้วยชุดย่อยของตัวแปรทำนายในโมเดลการถดถอยโดยรวม
ตัวอย่างเช่น สมมติว่าเรามีแบบจำลองการถดถอยต่อไปนี้ซึ่งมีตัวแปรทำนายสี่ตัว:
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
ตัวอย่างของโมเดลที่ซ้อนกันจะเป็นโมเดลต่อไปนี้ซึ่งมีตัวแปรทำนายดั้งเดิมเพียงสองตัวเท่านั้น:
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
เพื่อตรวจสอบว่าทั้งสองแบบจำลองนี้มีความแตกต่างกันอย่างมีนัยสำคัญหรือไม่ เราสามารถทำการทดสอบ F-test บางส่วนได้ ซึ่งจะคำนวณสถิติการทดสอบ F ต่อไปนี้:
F = (( RSS ที่ลดลง – RSS เต็ม )/p) / ( RSS เต็ม /nk)
ทอง:
- RSS ที่ลดลง : ผลรวมที่เหลือของกำลังสองของโมเดลรีดิวซ์ (เช่น “ซ้อนกัน”)
- RSS เต็ม : ผลรวมที่เหลือของกำลังสองของแบบจำลองเต็ม
- p: จำนวนตัวทำนายที่ถูกลบออกจากโมเดลเต็ม
- n: จำนวนการสังเกตทั้งหมดในชุดข้อมูล
- k: จำนวนสัมประสิทธิ์ (รวมจุดตัด) ในแบบจำลองเต็ม
การทดสอบนี้ใช้ สมมติฐาน ว่างและทางเลือกต่อไปนี้:
H 0 : ค่าสัมประสิทธิ์ทั้งหมดที่ถอดออกจากแบบจำลองเต็มจะเป็นศูนย์
HA : ค่าสัมประสิทธิ์อย่างน้อยหนึ่งค่าที่ถูกลบออกจากแบบจำลองที่สมบูรณ์นั้นไม่เป็นศูนย์
หาก ค่า p ที่สอดคล้องกับสถิติการทดสอบ F ต่ำกว่าระดับนัยสำคัญที่กำหนด (เช่น 0.05) เราก็สามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่าค่าสัมประสิทธิ์อย่างน้อยหนึ่งค่าที่ถูกลบออกจากแบบจำลองแบบเต็มนั้นมีนัยสำคัญ
ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการทดสอบ F บางส่วนใน Excel
ตัวอย่าง: การทดสอบ F บางส่วนใน Excel
สมมติว่าเรามีชุดข้อมูลต่อไปนี้ใน Excel:
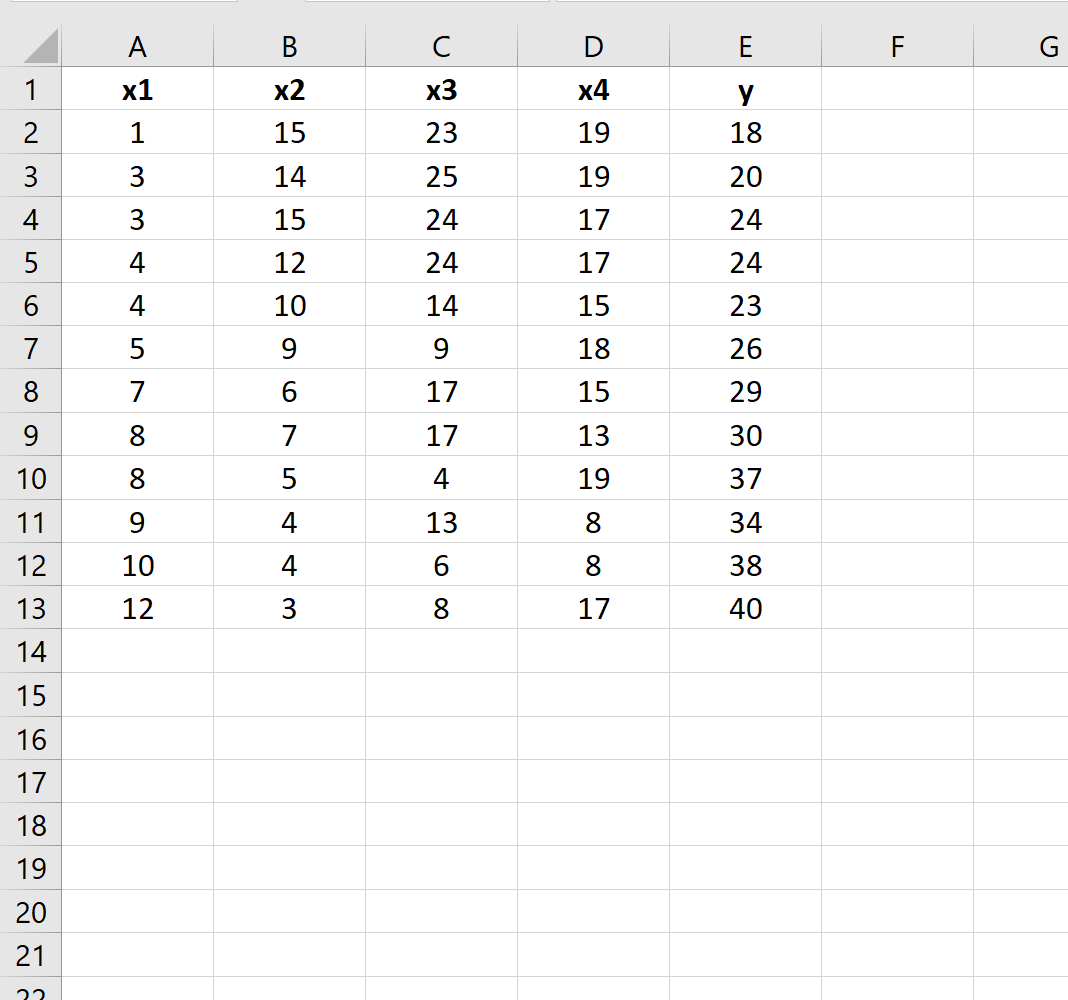
สมมติว่าเราต้องการตรวจสอบว่ามีความแตกต่างระหว่างแบบจำลองการถดถอยสองแบบต่อไปนี้หรือไม่:
โมเดลที่สมบูรณ์: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
โมเดลที่ลดลง: y = β 0 + β 1 x 1 + β 2 x 2
เราสามารถทำการ ถดถอยเชิงเส้นหลายรายการใน Excel สำหรับแต่ละรุ่นเพื่อให้ได้ผลลัพธ์ต่อไปนี้:
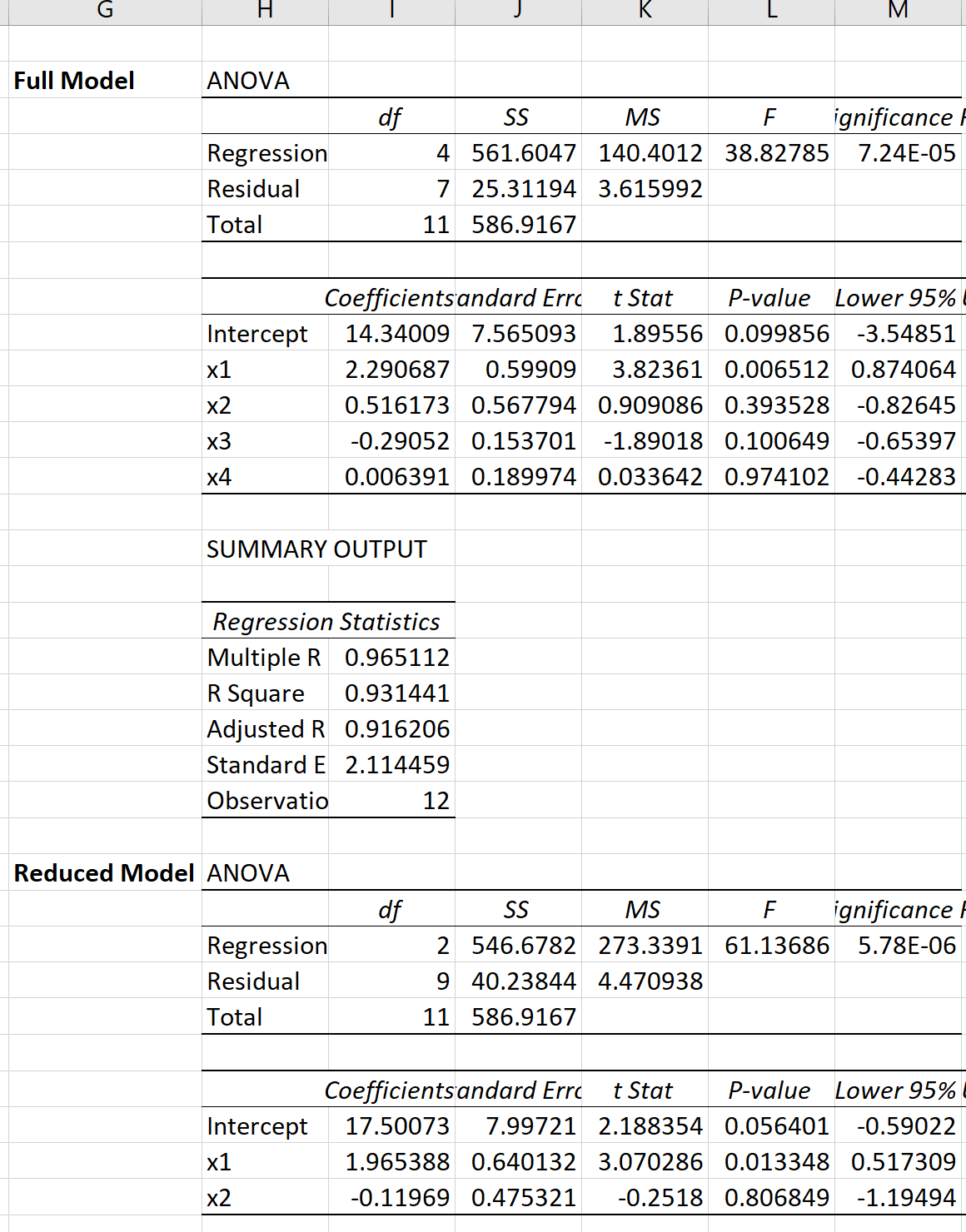
จากนั้นเราสามารถใช้สูตรต่อไปนี้เพื่อคำนวณสถิติการทดสอบ F สำหรับการทดสอบ F บางส่วน:
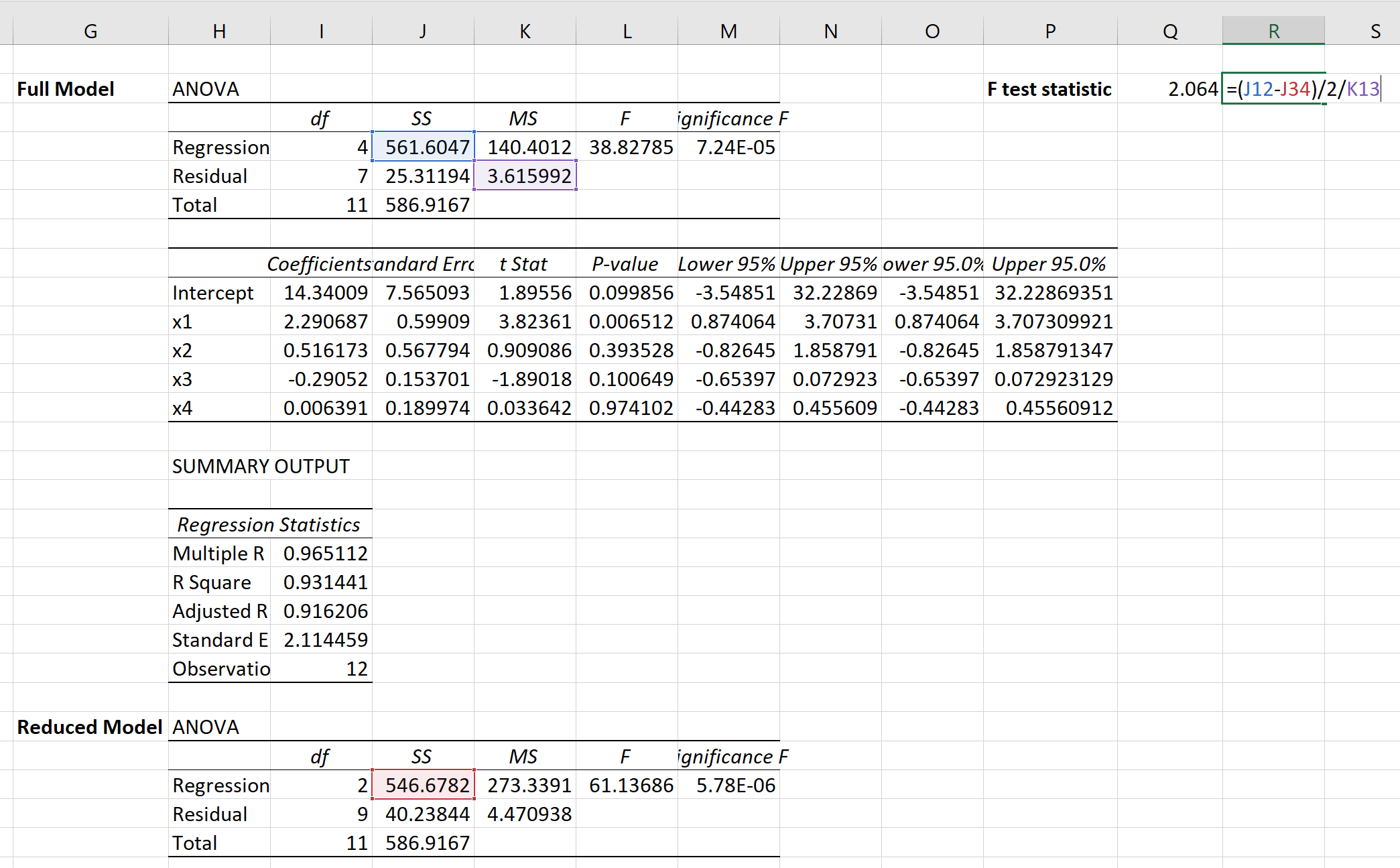
สถิติการทดสอบกลายเป็น 2.064
จากนั้นเราสามารถใช้สูตรต่อไปนี้เพื่อคำนวณค่า p ที่สอดคล้องกัน:
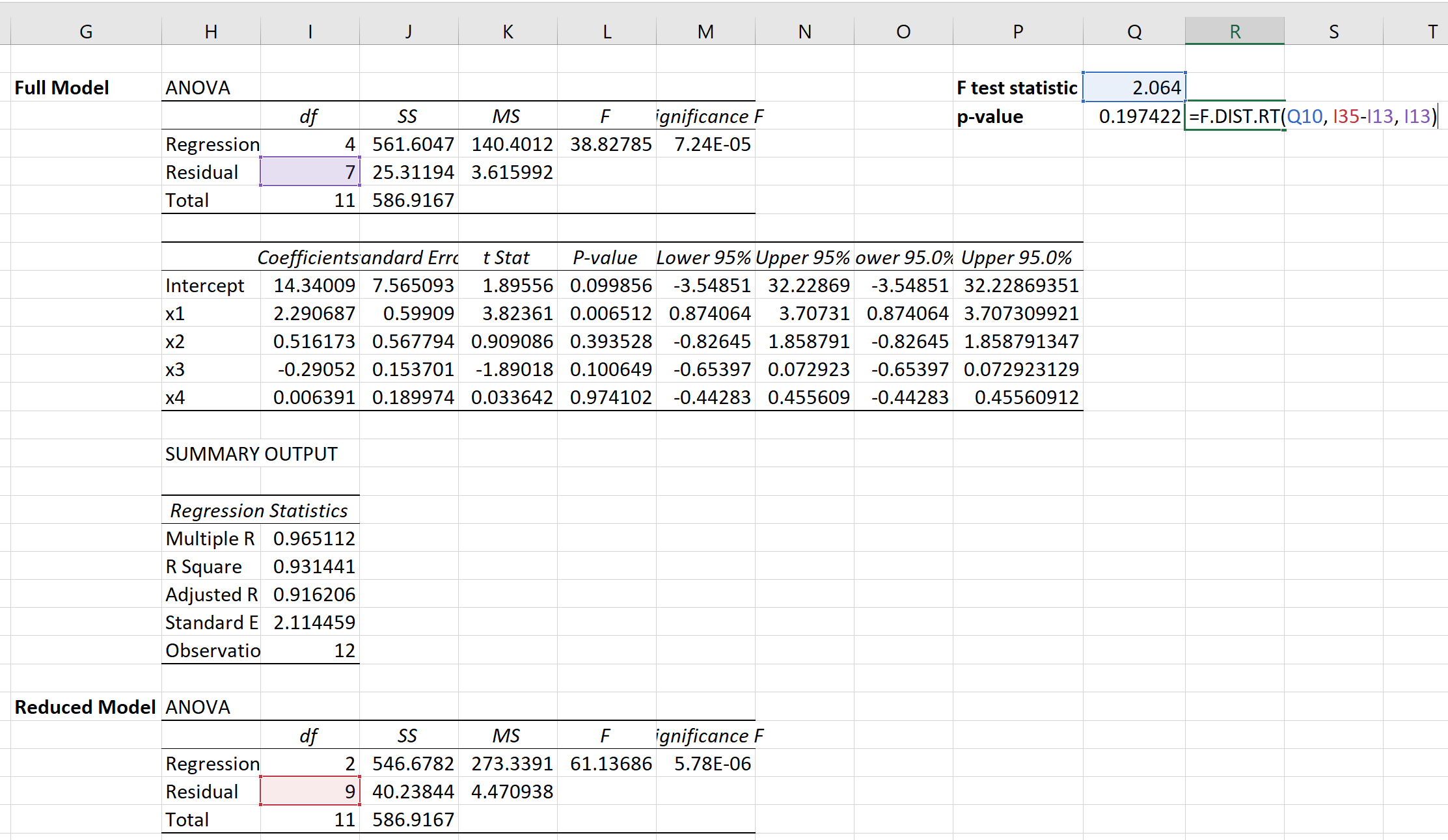
ค่า p กลายเป็น 0.1974
เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะบอกว่าตัวแปรตัวทำนาย x3 หรือ x4 ตัวใดตัวหนึ่งมีนัยสำคัญทางสถิติ
กล่าวอีกนัยหนึ่ง การเพิ่ม x3 และ x4 ให้กับโมเดลการถดถอยไม่ได้ช่วยปรับปรุงความพอดีของโมเดลอย่างมีนัยสำคัญ
แหล่งข้อมูลเพิ่มเติม
วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน Excel
วิธีการดำเนินการถดถอยเชิงเส้นหลายรายการใน Excel
วิธีการคำนวณข้อผิดพลาดมาตรฐานของการถดถอยใน Excel
เกี่ยวกับผู้แต่ง
ดร.เบนจามิน แอนเดอร์สัน
สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม