การปรับเส้นโค้งใน excel (พร้อมตัวอย่าง)
บ่อยครั้งคุณอาจต้องการค้นหาสมการที่เหมาะกับเส้นโค้งสำหรับชุดข้อมูลใน Excel มากที่สุด
โชคดีที่การใช้ฟังก์ชัน Trendline ของ Excel ทำได้ค่อนข้างง่าย
บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีปรับสมการให้พอดีกับเส้นโค้งใน Excel
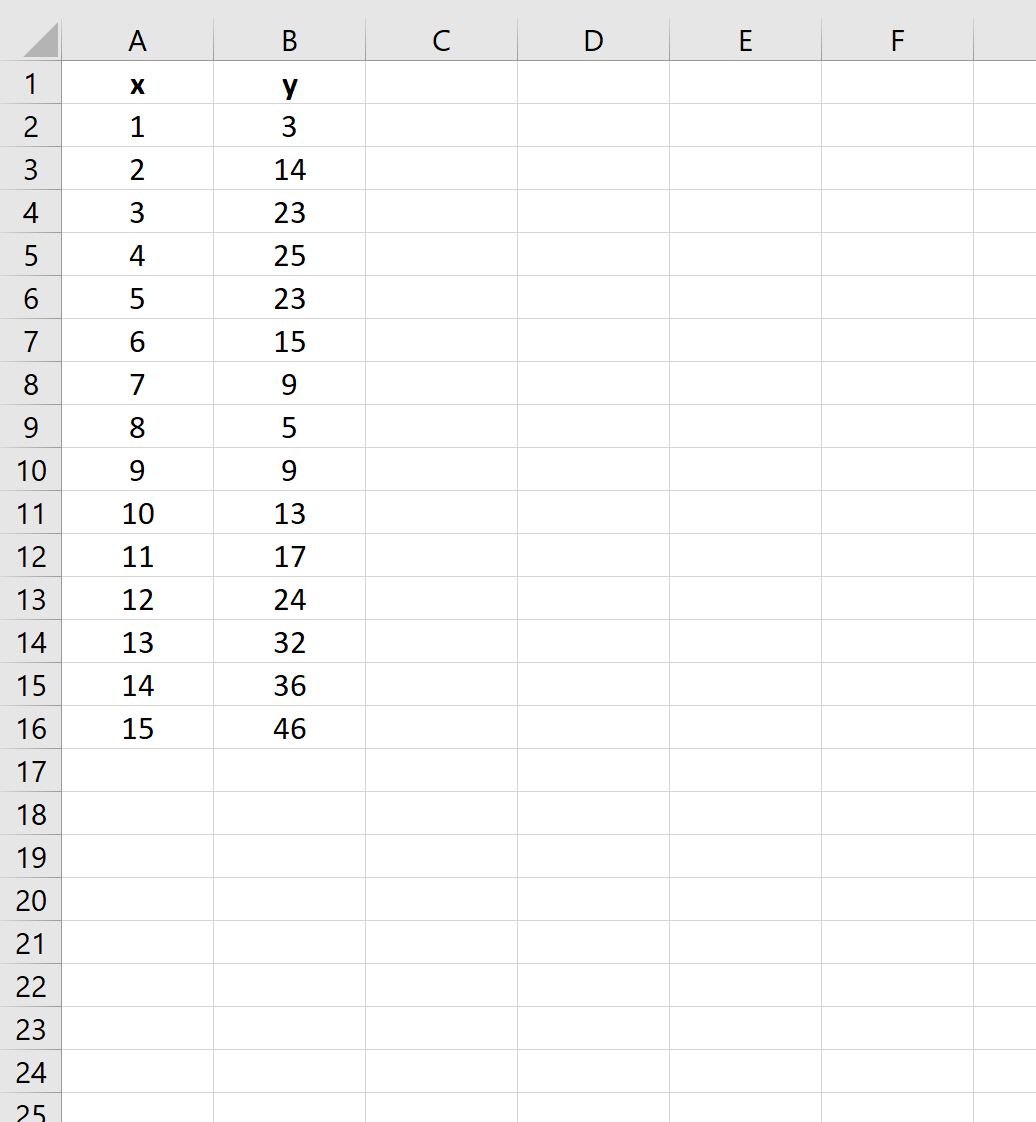
ขั้นตอนที่ 1: สร้างข้อมูล
ขั้นแรก เรามาสร้างชุดข้อมูลปลอมเพื่อใช้งานกับ:
ขั้นตอนที่ 2: สร้างแผนภูมิกระจาย
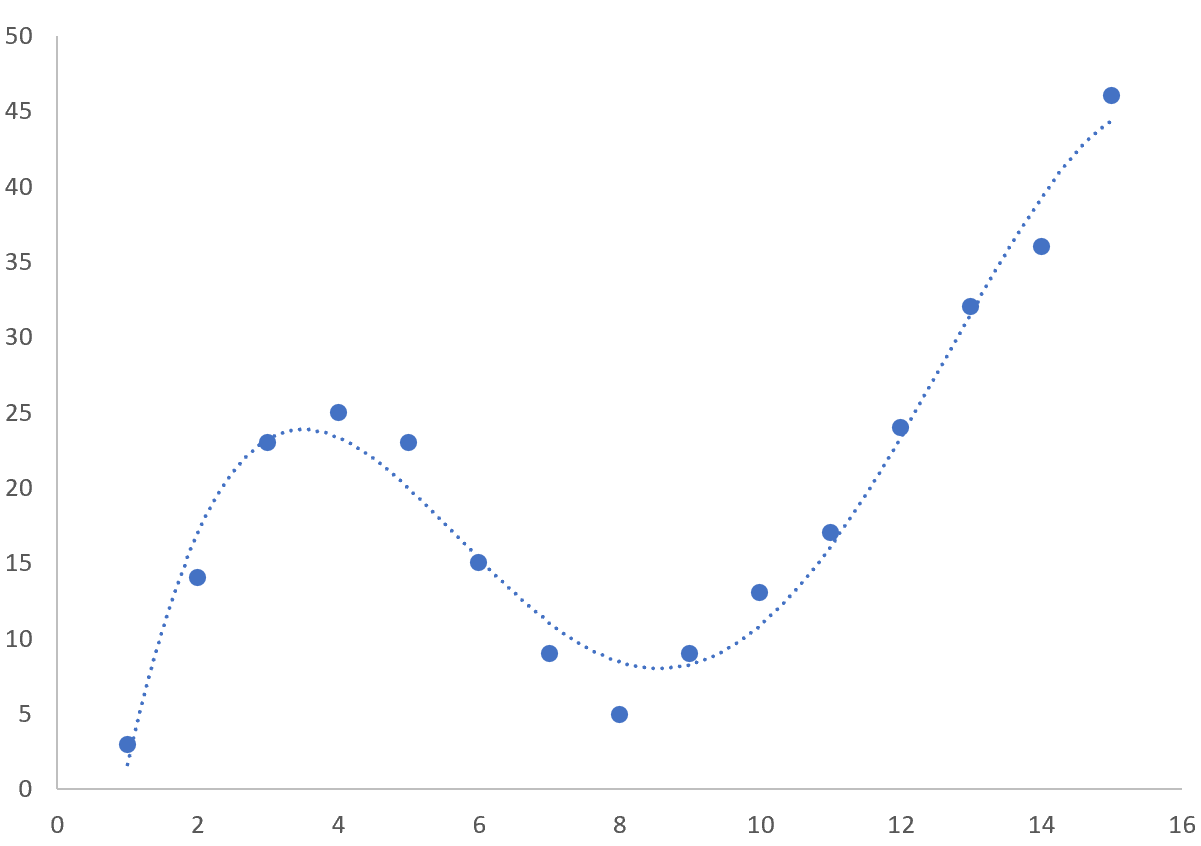
ต่อไป เรามาสร้าง Scatterplot เพื่อแสดงภาพชุดข้อมูลกัน
ขั้นแรก ไฮไลต์เซลล์ A2:B16 ดังนี้:
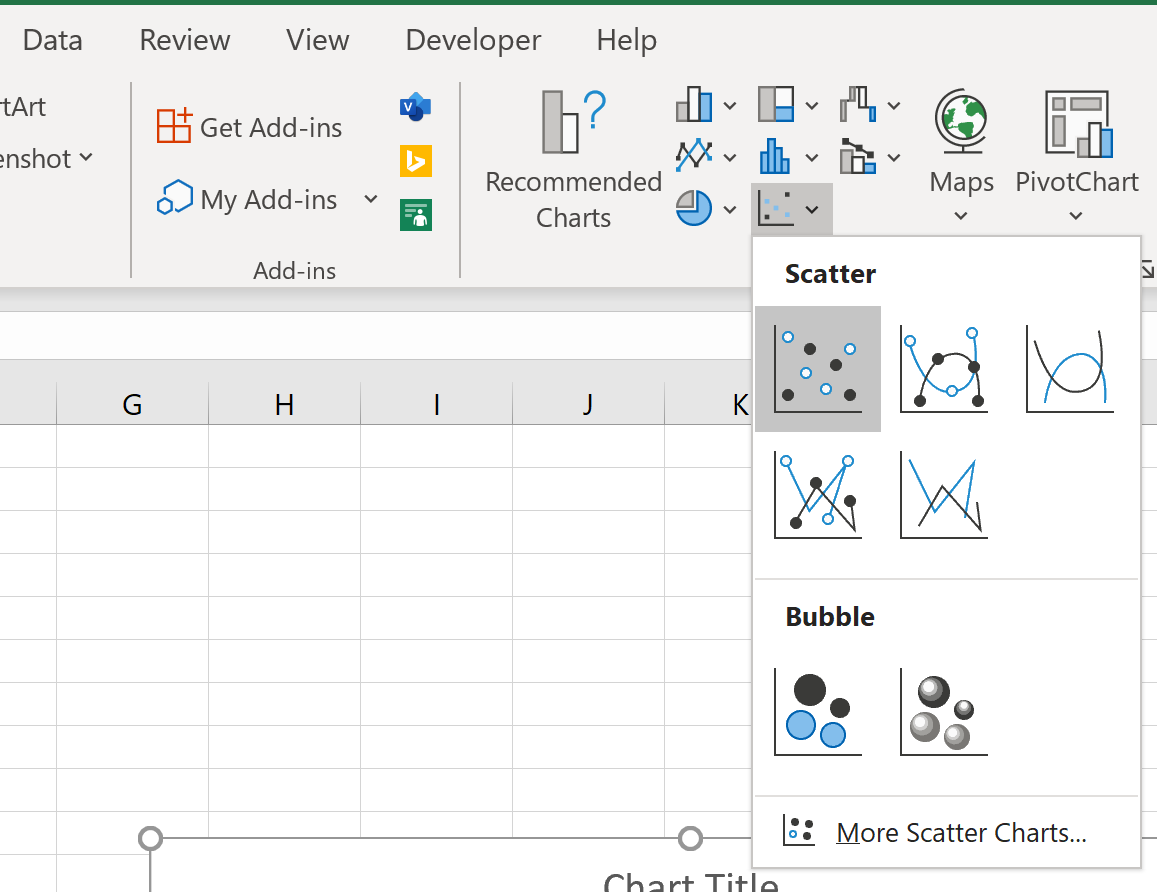
จากนั้นคลิกแท็บ แทรก ที่ริบบิ้นด้านบน จากนั้นคลิกตัวเลือกการลงจุดแรกใต้ Scatter :
สิ่งนี้จะสร้างพล็อตกระจายต่อไปนี้:
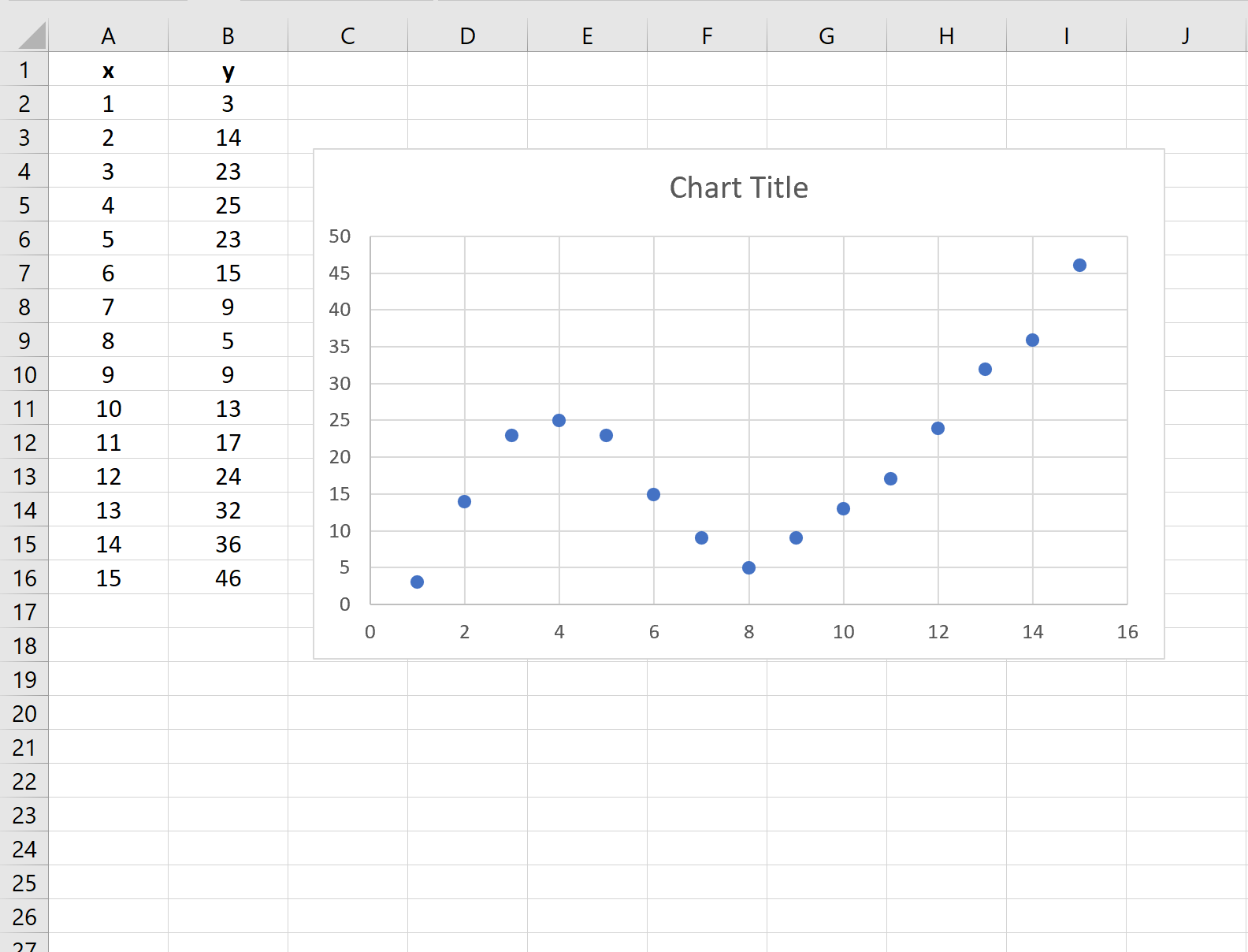
ขั้นตอนที่ 3: เพิ่มเส้นแนวโน้ม
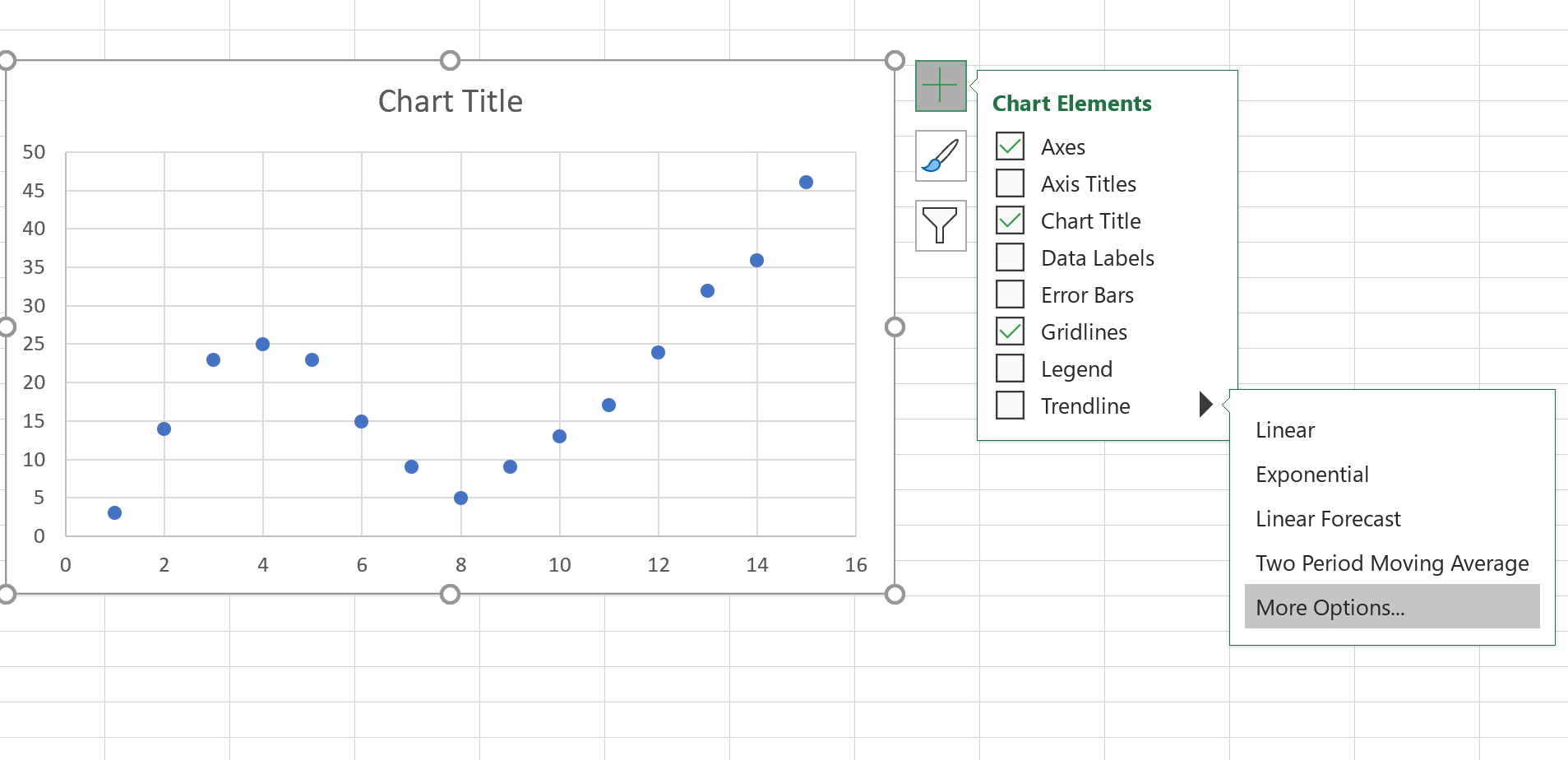
จากนั้นคลิกที่ใดก็ได้บน Scatterplot จากนั้นคลิกที่เครื่องหมาย + ที่มุมขวาบน ในเมนูแบบเลื่อนลง คลิกลูกศรถัดจาก เส้นแนวโน้ม จากนั้นคลิก ตัวเลือกเพิ่มเติม :
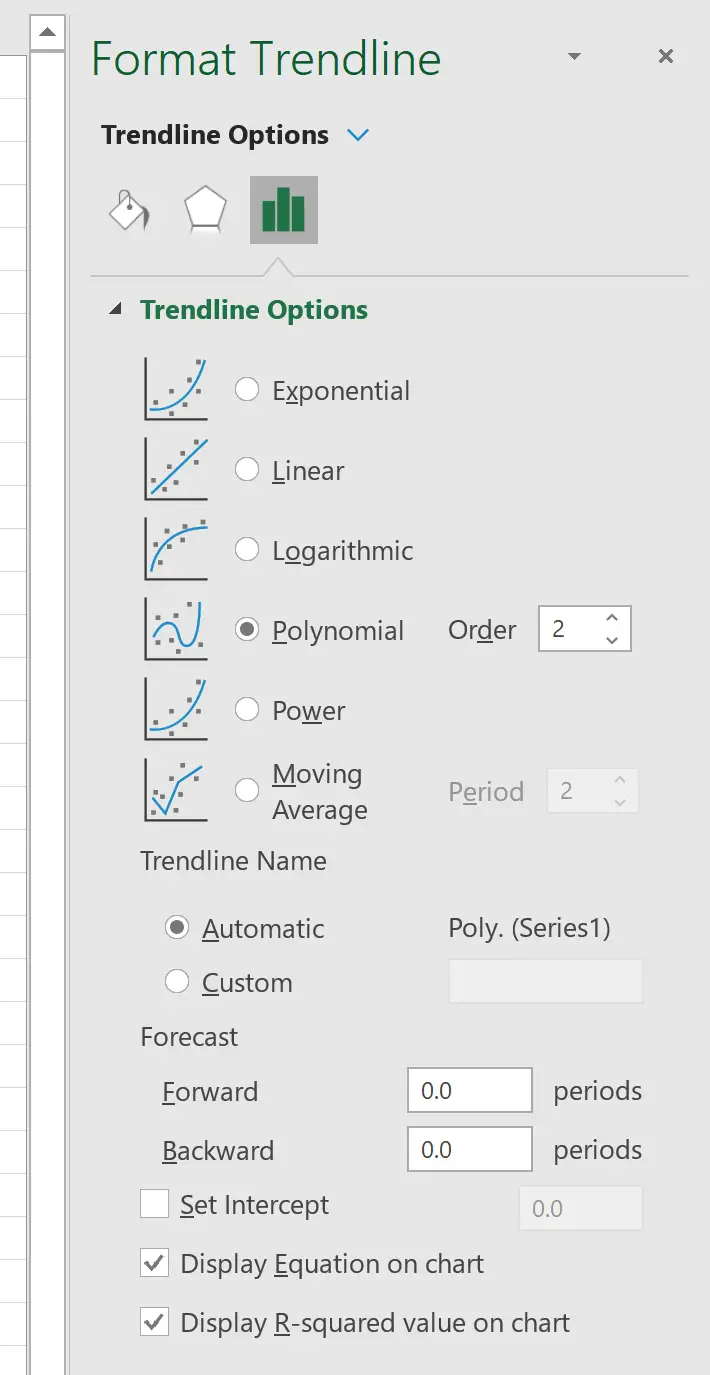
ในหน้าต่างที่ปรากฏทางด้านขวา ให้คลิกปุ่มถัดจาก พหุนาม จากนั้นทำเครื่องหมายที่ช่องถัดจาก แสดงสมการบนแผนภูมิ และ แสดงค่า R-squared บนแผนภูมิ
สิ่งนี้จะสร้างเส้นโค้งต่อไปนี้บนพอยต์คลาวด์:
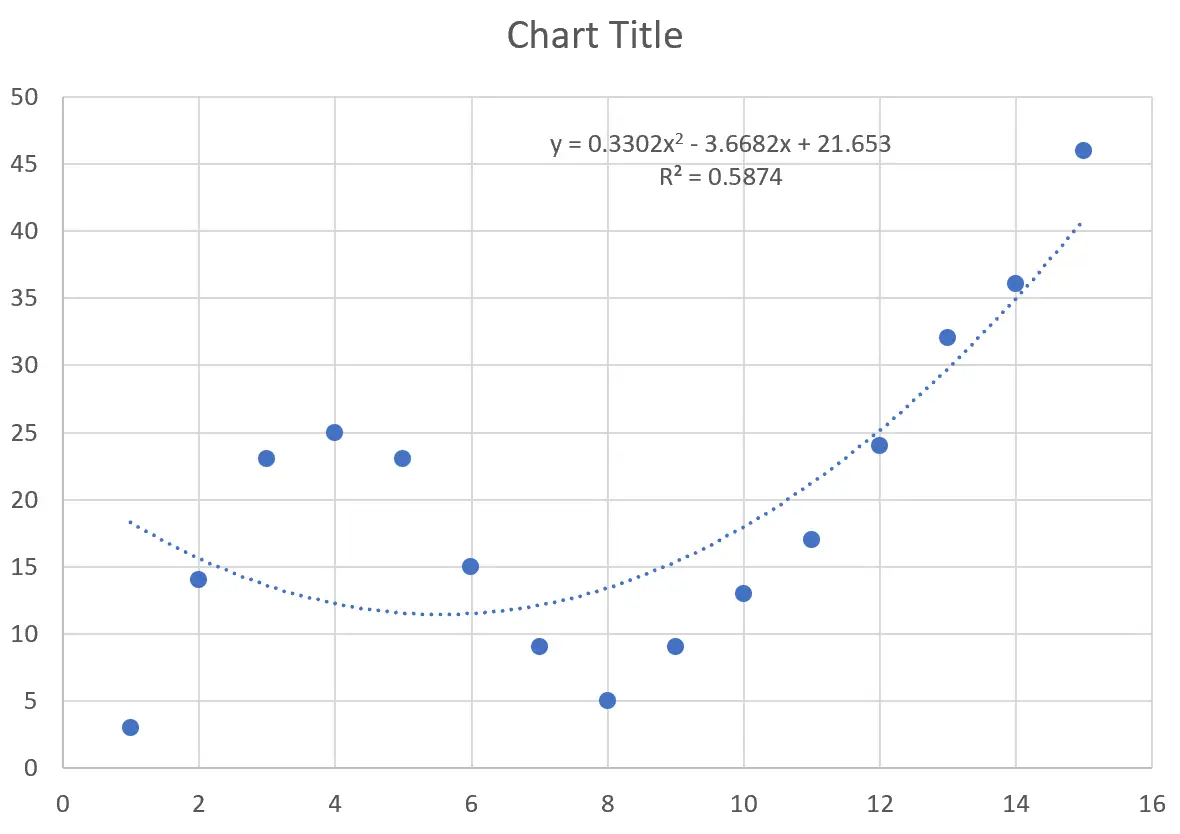
สมการของเส้นโค้งมีดังนี้:
y = 0.3302x 2 – 3.6682x + 21.653
R-squared บอกเราถึงเปอร์เซ็นต์ของการแปรผันใน ตัวแปรตอบสนอง ที่ตัวแปรทำนายสามารถอธิบายได้ R กำลังสองสำหรับเส้นโค้งนี้คือ 0.5874
ขั้นตอนที่ 4: เลือกเส้นแนวโน้มที่ดีที่สุด
นอกจากนี้เรายังสามารถเพิ่มลำดับของพหุนามที่เราใช้เพื่อดูว่าเส้นโค้งที่ยืดหยุ่นมากขึ้นนั้นเหมาะสมกับชุดข้อมูลมากกว่าหรือไม่
ตัวอย่างเช่น เราอาจเลือกที่จะตั้งค่าลำดับพหุนามเป็น 4:
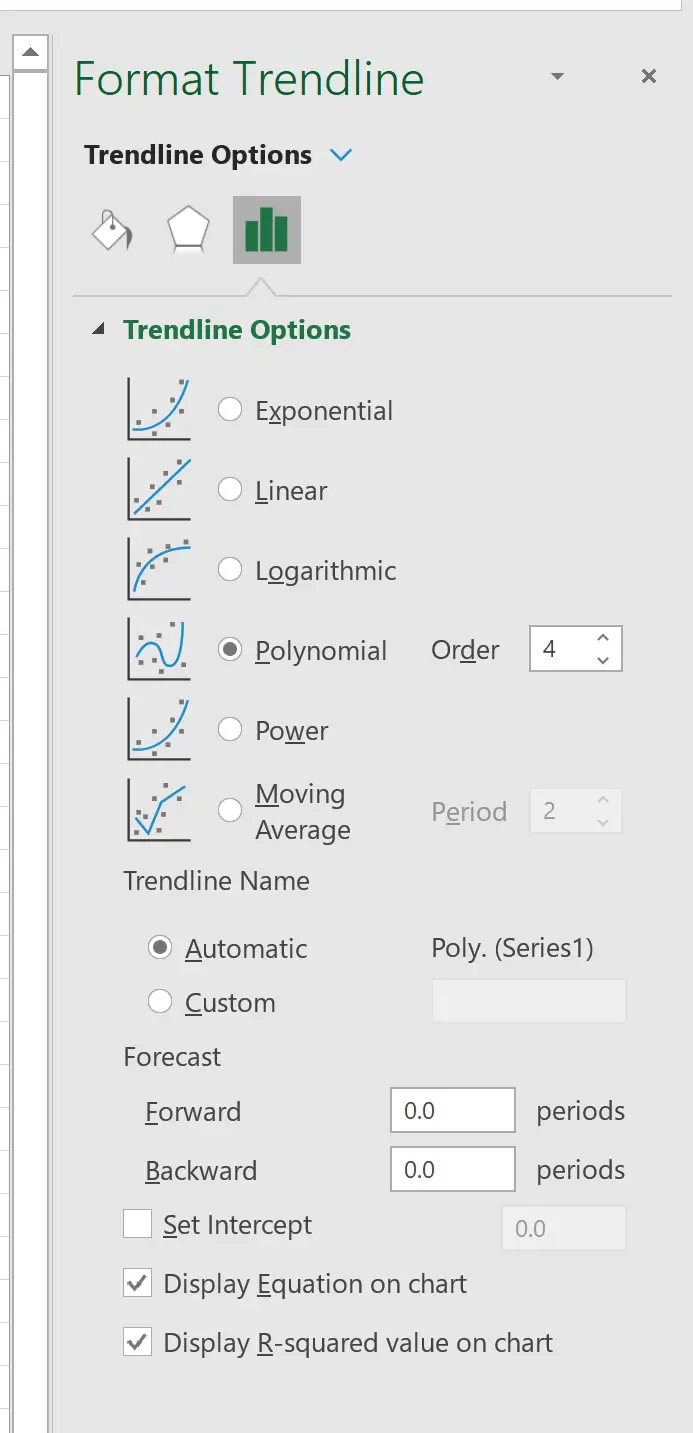
ผลลัพธ์ที่ได้คือเส้นโค้งต่อไปนี้:
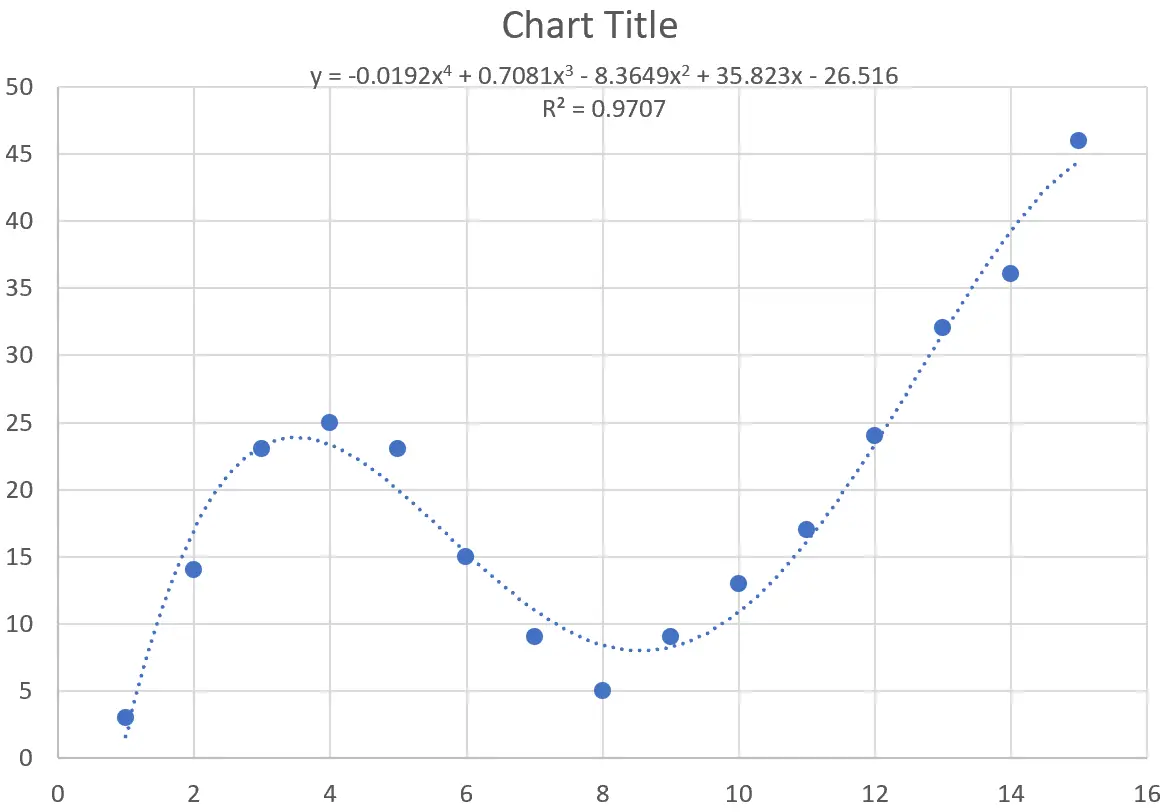
สมการของเส้นโค้งมีดังนี้:
y = -0.0192x 4 + 0.7081x 3 – 8.3649x 2 + 35.823x – 26.516
R กำลังสองสำหรับเส้นโค้งนี้คือ 0.9707
R-squared นี้สูงกว่าเส้นโค้งก่อนหน้าอย่างมาก ซึ่งบ่งชี้ว่าตรงกับชุดข้อมูลอย่างใกล้ชิดมากขึ้น
นอกจากนี้เรายังสามารถใช้สมการเส้นโค้งนี้เพื่อทำนายค่าของตัวแปรตอบสนองตามตัวแปรทำนาย ตัวอย่างเช่น ถ้า x = 4 เราก็จะทำนายว่า y = 23.34 :
y = -0.0192(4) 4 + 0.7081(4) 3 – 8.3649(4) 2 + 35.823(4) – 26.516 = 23.34
คุณสามารถค้นหาบทช่วยสอน Excel เพิ่มเติมได้ใน หน้านี้