กำลังพิมพ์
บทความนี้จะอธิบายว่าการระบุลักษณะการกระจายตัวในสถิติหมายความว่าอย่างไร ดังนั้นคุณจะพบคำจำกัดความของการพิมพ์ ตัวอย่างการพิมพ์ของตัวแปร และนอกจากนี้ คุณจะสามารถฝึกฝนโดยแก้ไขแบบฝึกหัดทีละขั้นตอนได้
กำลังพิมพ์อะไรอยู่?
ในสถิติ การ ทำให้เป็นมาตรฐาน เป็นกระบวนการที่ใช้การแปลงเชิงเส้นกับการแจกแจง โดยให้ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเท่ากับศูนย์และหนึ่ง ตามลำดับ
แม่นยำยิ่งขึ้น การพิมพ์เกี่ยวข้องกับการลบค่าเฉลี่ยออกจากตัวแปรสุ่มแล้วหารด้วยค่าเบี่ยงเบนมาตรฐาน
การพิมพ์อาจเรียกว่าการทำให้เป็นมาตรฐานหรือการทำให้เป็นมาตรฐาน
สูตรอินพุต
หากต้องการจำแนกตัวแปร คุณต้องลบค่าเฉลี่ยแล้วหารด้วยค่าเบี่ยงเบนมาตรฐาน สูตรการป้อน ตัวแปรจึงเป็นดังนี้:
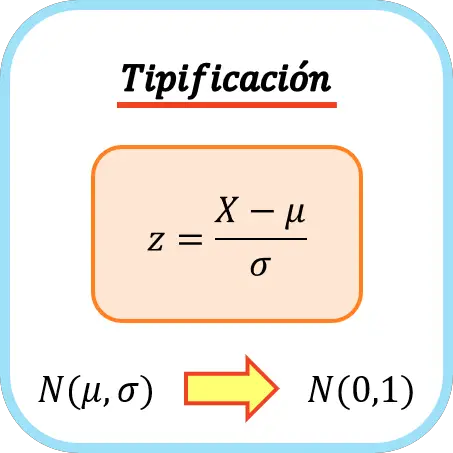
ทอง
![]()
คือค่าเฉลี่ยของตัวแปร
![]()
และ
![]()
ส่วนเบี่ยงเบนมาตรฐาน (หรือส่วนเบี่ยงเบนมาตรฐาน)
ดังนั้น จริงๆ แล้วรายการจึงเป็นการเปลี่ยนแปลงตัวแปร เนื่องจากมีการนำการแปลงเชิงเส้นไปใช้กับตัวแปร
ตัวอย่างรายการ
เมื่อพิจารณาถึงคำจำกัดความของการพิมพ์และสูตร ด้านล่างนี้เป็นตัวอย่างที่เป็นรูปธรรมเพื่อทำความเข้าใจแนวคิดนี้อย่างถ่องแท้
- ตัวแปรสุ่มต่อเนื่องเป็นไปตามการแจกแจงแบบปกติโดยมีค่าเฉลี่ย 45 และส่วนเบี่ยงเบนมาตรฐาน 10 ความน่าจะเป็นที่จะได้ค่าน้อยกว่าหรือเท่ากับ 60 เป็นเท่าใด
![]()
ในการค้นหาความน่าจะเป็นของการแจกแจงแบบปกติ เราจำเป็นต้องใช้ตารางคุณลักษณะของมัน แต่ในการทำเช่นนี้ เราจำเป็นต้องดำเนินการพิมพ์ก่อน ดังนั้นเราจึงลบค่าเฉลี่ยแล้วหารด้วยค่าเบี่ยงเบนมาตรฐานเป็นค่าความน่าจะเป็น:
![]()
เมื่อเราได้มาตรฐานแล้ว เราจะไปยังตารางความน่าจะเป็นของการแจกแจงแบบปกติเพื่อดูว่าค่าความน่าจะเป็นของ 1.5 สอดคล้องกับค่าใด:

ดังที่เห็นในตารางประเภทการแจกแจงแบบปกติ ค่าที่คำนวณในขั้นตอนก่อนหน้าจะสอดคล้องกับความน่าจะเป็นต่อไปนี้:
![]()
ความน่าจะเป็นที่จะได้ค่าเท่ากับหรือน้อยกว่า 60 จึงเป็น 93.32%
แบบฝึกหัดการพิมพ์แก้ไขแล้ว
คำนวณความน่าจะเป็นของการแจกแจงแบบปกติซึ่งมีค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเป็น 120 และ 50 ตามลำดับต่อไปนี้
![]()
- ความน่าจะเป็นที่จะได้ค่าน้อยกว่าหรือเท่ากับ 208
- ความน่าจะเป็นที่จะได้ค่าที่มากกว่า 137
ในทั้งสองส่วนของปัญหา เราต้องพิมพ์การแจกแจงแบบปกติเพื่อคำนวณความน่าจะเป็น
เราเริ่มต้นด้วยการคำนวณการพิมพ์ความน่าจะเป็นของค่าที่น้อยกว่าหรือเท่ากับ 208:
![]()
และตอนนี้เรามาดูตารางด้านบนว่าค่า 1.76 สอดคล้องกับความน่าจะเป็นเท่าใด:
![]()
ประการที่สอง เราจะคำนวณความน่าจะเป็นที่จะได้ค่าที่มากกว่า 137 ในทำนองเดียวกัน เราเริ่มต้นด้วยการพิมพ์ตัวแปร:
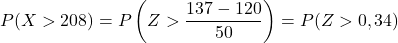 อย่างไรก็ตาม ตารางที่แนบมามีเพียงความน่าจะเป็นสะสมที่ต่ำที่สุดเท่านั้น ดังนั้นในการใช้ตาราง เราต้องแปลงความน่าจะเป็นก่อน:
อย่างไรก็ตาม ตารางที่แนบมามีเพียงความน่าจะเป็นสะสมที่ต่ำที่สุดเท่านั้น ดังนั้นในการใช้ตาราง เราต้องแปลงความน่าจะเป็นก่อน:
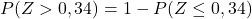 และสุดท้าย เราจะสังเกตจากตารางที่แนบมานี้ถึงความน่าจะเป็นที่สอดคล้องกับค่าที่คำนวณได้ของ Z:
และสุดท้าย เราจะสังเกตจากตารางที่แนบมานี้ถึงความน่าจะเป็นที่สอดคล้องกับค่าที่คำนวณได้ของ Z:
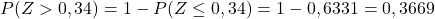
ประเด็นในการพิมพ์คืออะไร?
เพื่อทำความเข้าใจความหมายของการพิมพ์ให้เสร็จสิ้น เราจะมาดูกันว่ามีไว้เพื่ออะไร และเมื่อใดที่จะต้องพิมพ์ตัวแปร
โดยหลักๆ แล้ว การกำหนดมาตรฐานใช้เพื่อเปรียบเทียบค่าของการแจกแจงด้วยวิธีการและความแปรปรวนที่แตกต่างกัน ในทำนองเดียวกัน การกำหนดมาตรฐานยังใช้ในการคำนวณความน่าจะเป็นด้วย
ด้วยการกำหนดมาตรฐานการแจกแจงสองค่าด้วยคุณลักษณะที่แตกต่างกัน เราจะเห็นได้ว่าค่าใดมากกว่าหรือน้อยกว่าเมื่อเทียบกับการแจกแจงทั้งหมด หรืออีกนัยหนึ่ง โดยการใช้กระบวนการพิมพ์ เราจะเห็นว่าค่าใดอยู่ใกล้หรือไกลที่สุดจากค่าเฉลี่ยของการแจกแจง
นอกจากนี้ ตามที่อธิบายไว้ข้างต้น การพิมพ์ยังช่วยให้สามารถคำนวณความน่าจะเป็นได้ เนื่องจากโดยทั่วไปตารางความน่าจะเป็นจะขึ้นอยู่กับการแจกแจงแบบพิมพ์