วิธีการดำเนินการวัดความแปรปรวนซ้ำใน spss

การวัดความแปรปรวนแบบวัดซ้ำ จะถูกนำมาใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มตั้งแต่สามกลุ่มขึ้นไปซึ่งมีหัวข้อเดียวกันปรากฏในแต่ละกลุ่มหรือไม่

บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการวัดความแปรปรวนแบบทางเดียวซ้ำใน SPSS

ตัวอย่าง: การวัดความแปรปรวนซ้ำใน SPSS

นักวิจัยต้องการทราบว่ายาสี่ชนิดทำให้เกิดปฏิกิริยาต่างกันหรือไม่ เพื่อทดสอบสิ่งนี้ พวกเขาวัดเวลาปฏิกิริยาของผู้ป่วยห้ารายต่อยาสี่ชนิดที่แตกต่างกัน เนื่องจากผู้ป่วยแต่ละรายได้รับการวัดด้วยยาแต่ละชนิดจากทั้งหมดสี่ชนิด เราจะใช้การวัดความแปรปรวนแบบวัดซ้ำเพื่อตรวจสอบว่าเวลาเฉลี่ยของปฏิกิริยาแตกต่างกันระหว่างยาแต่ละชนิดหรือไม่

ทำตามขั้นตอนต่อไปนี้เพื่อดำเนินการวัดความแปรปรวนซ้ำใน SPSS

ขั้นตอนที่ 1: ป้อนข้อมูล

ป้อนข้อมูลต่อไปนี้ ซึ่งแสดงเวลาตอบสนอง (เป็นวินาที) ของผู้ป่วย 5 รายต่อยาทั้ง 4 ชนิด:

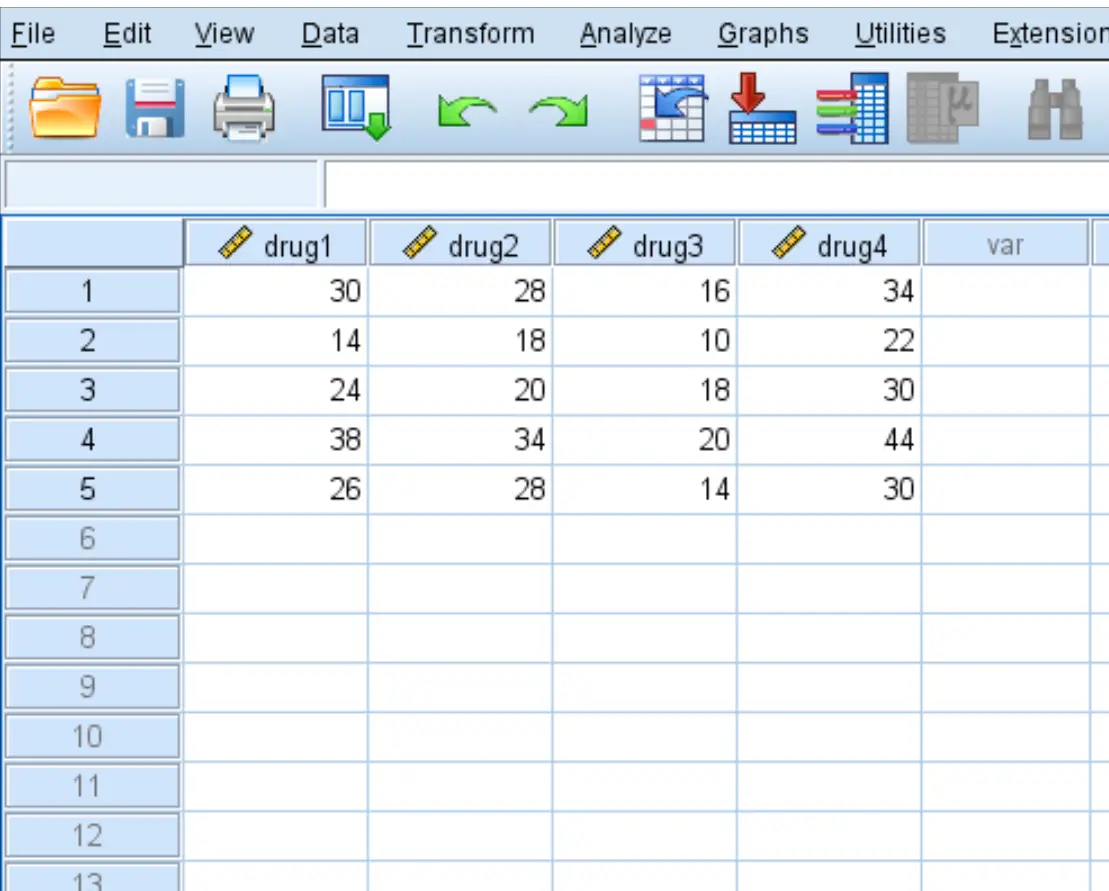
ขั้นตอนที่ 2: ทำการวัด ANOVA ซ้ำๆ

คลิกแท็บ วิเคราะห์ จากนั้นคลิก โมเดลเชิงเส้นทั่วไป จากนั้นคลิก การวัดซ้ำ :

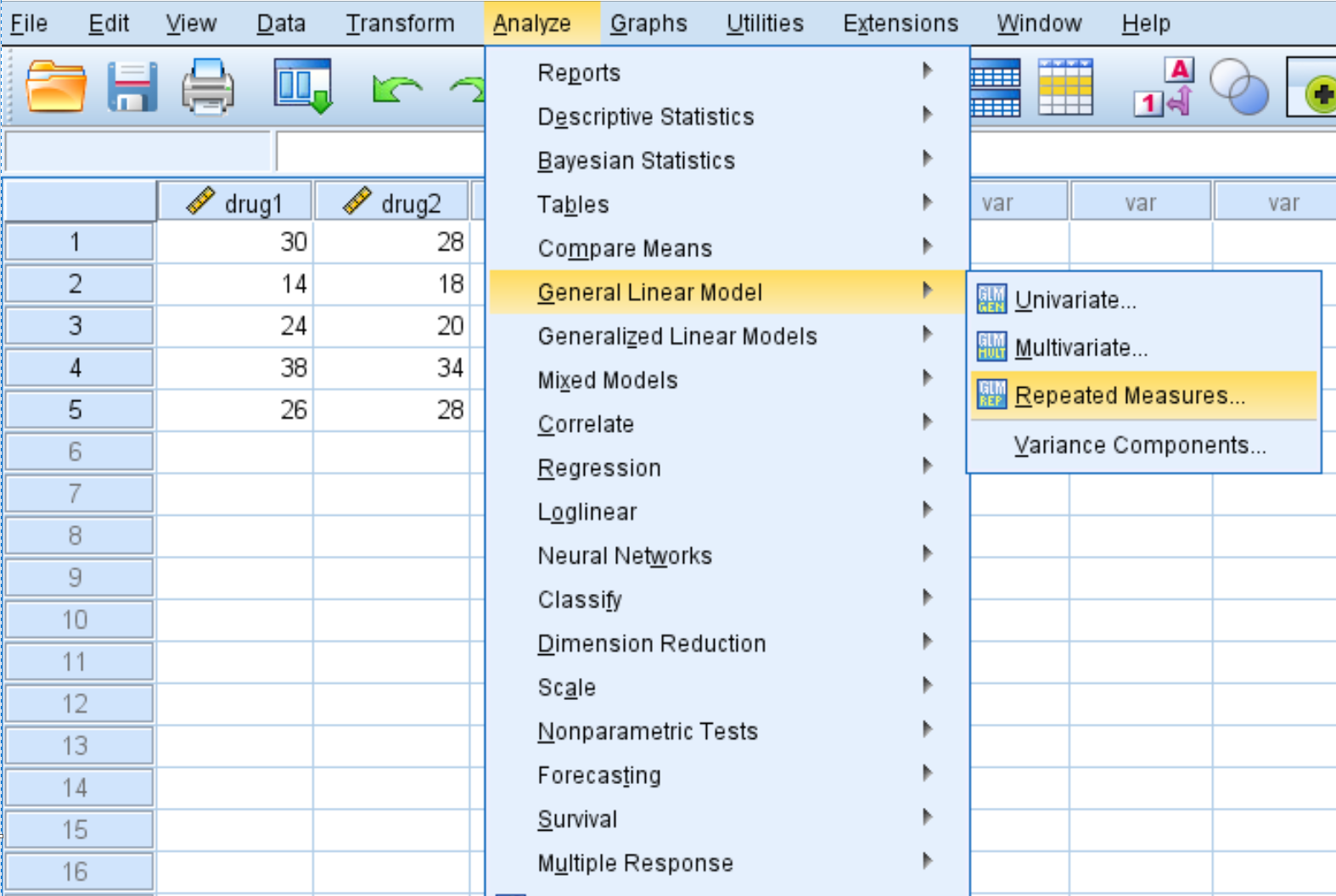
ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ป้อน ยา สำหรับชื่อปัจจัยภายในหัวเรื่อง พิมพ์จำนวนระดับ ที่ 4 (เนื่องจากแต่ละหัวข้อการศึกษาทดสอบยาที่แตกต่างกัน 4 ชนิด) จากนั้นจึงคลิก เพิ่ม พิมพ์ ResponseTime สำหรับ ชื่อการวัด และจากนั้น คลิก เพิ่ม สุดท้ายให้คลิก ตั้งค่า

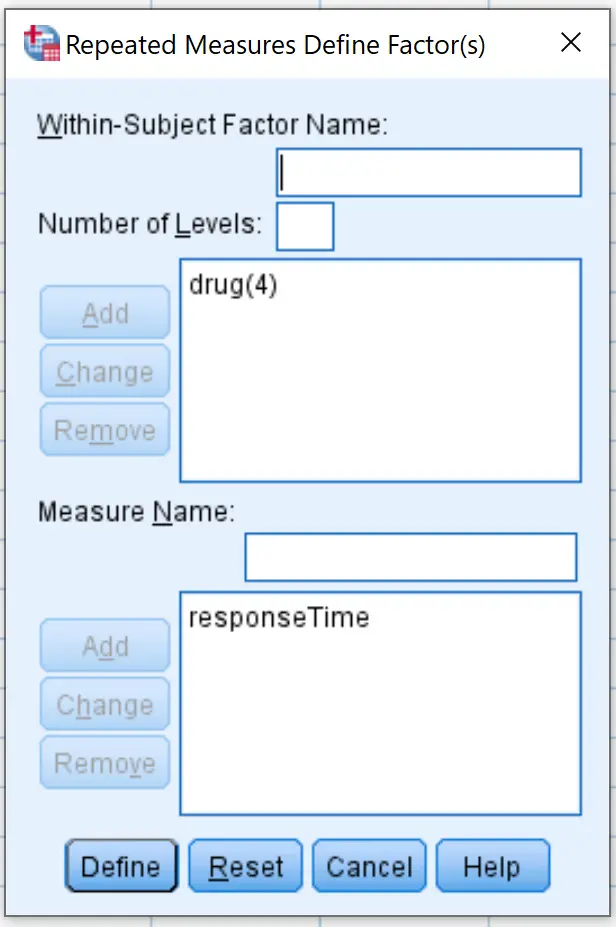
ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ลากตัวแปรยาทั้งสี่ตัวลงในพื้นที่ที่มีป้ายกำกับว่า Within-Subjects Variables :

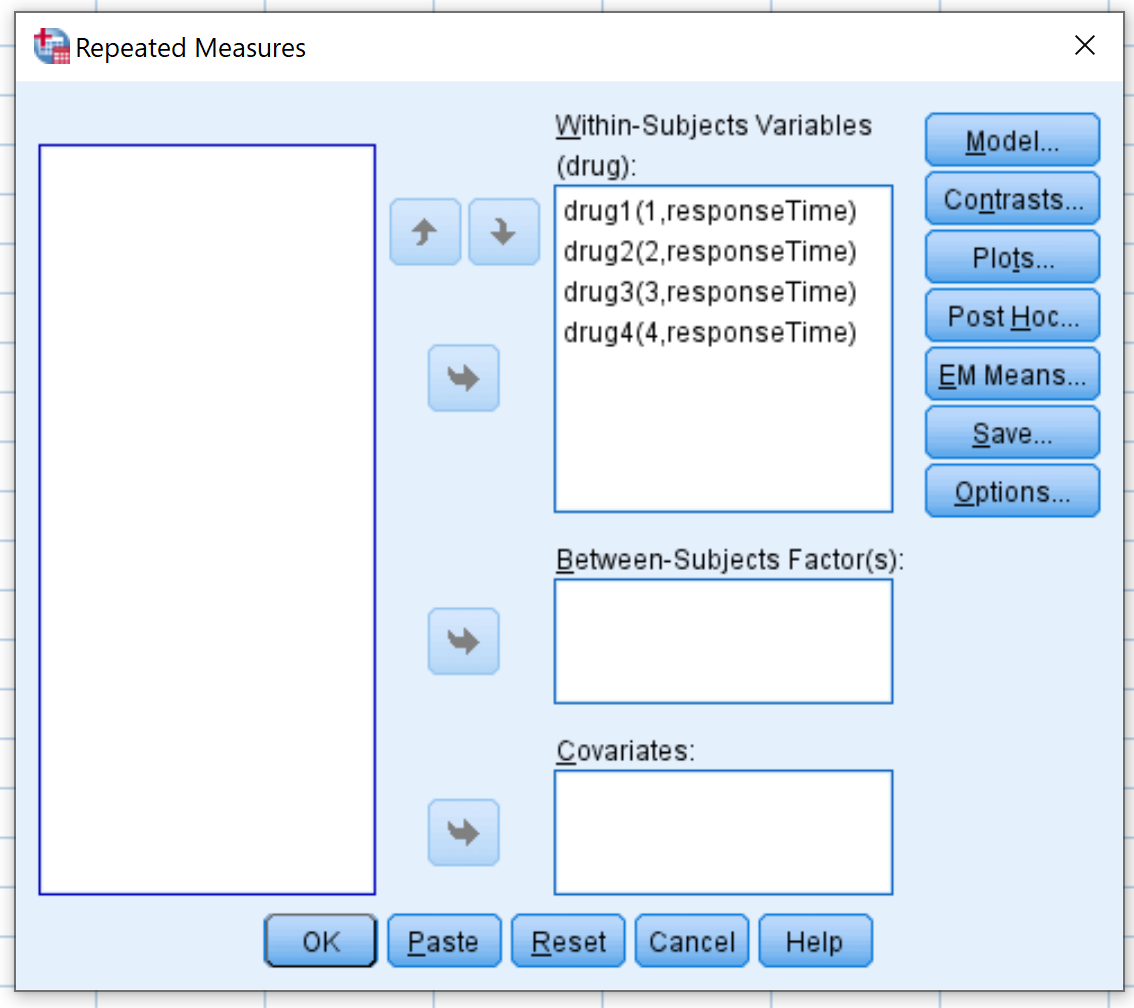
จากนั้นคลิก แปลง ลาก ยา แปรผันไปไว้ในพื้นที่ชื่อ แกนนอน จากนั้นคลิก เพิ่ม จากนั้นคลิก ดำเนินการต่อ

จากนั้นคลิก EM Means ลากตัวแปร ยา ลงในช่องที่ระบุว่า Show Means For จากนั้นทำเครื่องหมายที่ช่องถัดจาก เปรียบเทียบเอฟเฟกต์หลัก และเลือก Bonferroni จากเมนูแบบเลื่อนลง จากนั้นคลิก ดำเนินการต่อ

สุดท้ายคลิก ตกลง

ขั้นตอนที่ 2: ตีความผลลัพธ์

เมื่อคุณคลิก ตกลง ผลลัพธ์ของการวัดความแปรปรวนของการวัดซ้ำจะปรากฏขึ้น ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

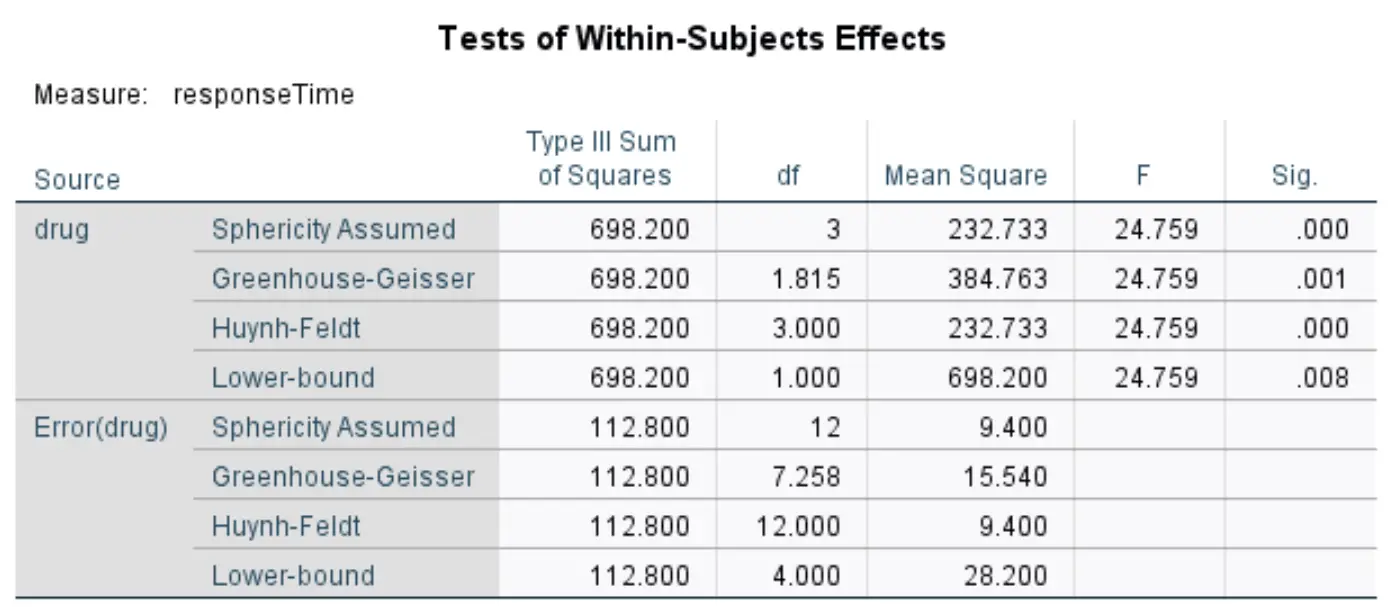
การทดสอบผลกระทบภายในวิชา

ตารางนี้แสดงสถิติ F โดยรวมและค่า p ที่สอดคล้องกันจากการวัด ANOVA ซ้ำ โดยทั่วไปเราใช้ค่าจากบรรทัดชื่อ Greenhouse-Geisser

ตามบรรทัดนี้ สถิติ F คือ 24.759 และค่า p ที่สอดคล้องกันคือ 0.001 เนื่องจากค่า p นี้น้อยกว่า 0.05 เราจึงสามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในเวลาตอบสนองโดยเฉลี่ยระหว่างยาทั้งสี่ชนิด

การเปรียบเทียบแบบคู่

เนื่องจากเราทิ้งสมมติฐานว่าง นั่นหมายความว่ามีค่าเฉลี่ยกลุ่มอย่างน้อย 2 อันที่แตกต่างกัน เพื่อพิจารณาว่ากลุ่มของค่าเฉลี่ยใดที่แตกต่างกัน เราสามารถใช้ตารางนี้ซึ่งแสดงการเปรียบเทียบแบบคู่ระหว่างยาแต่ละชนิด

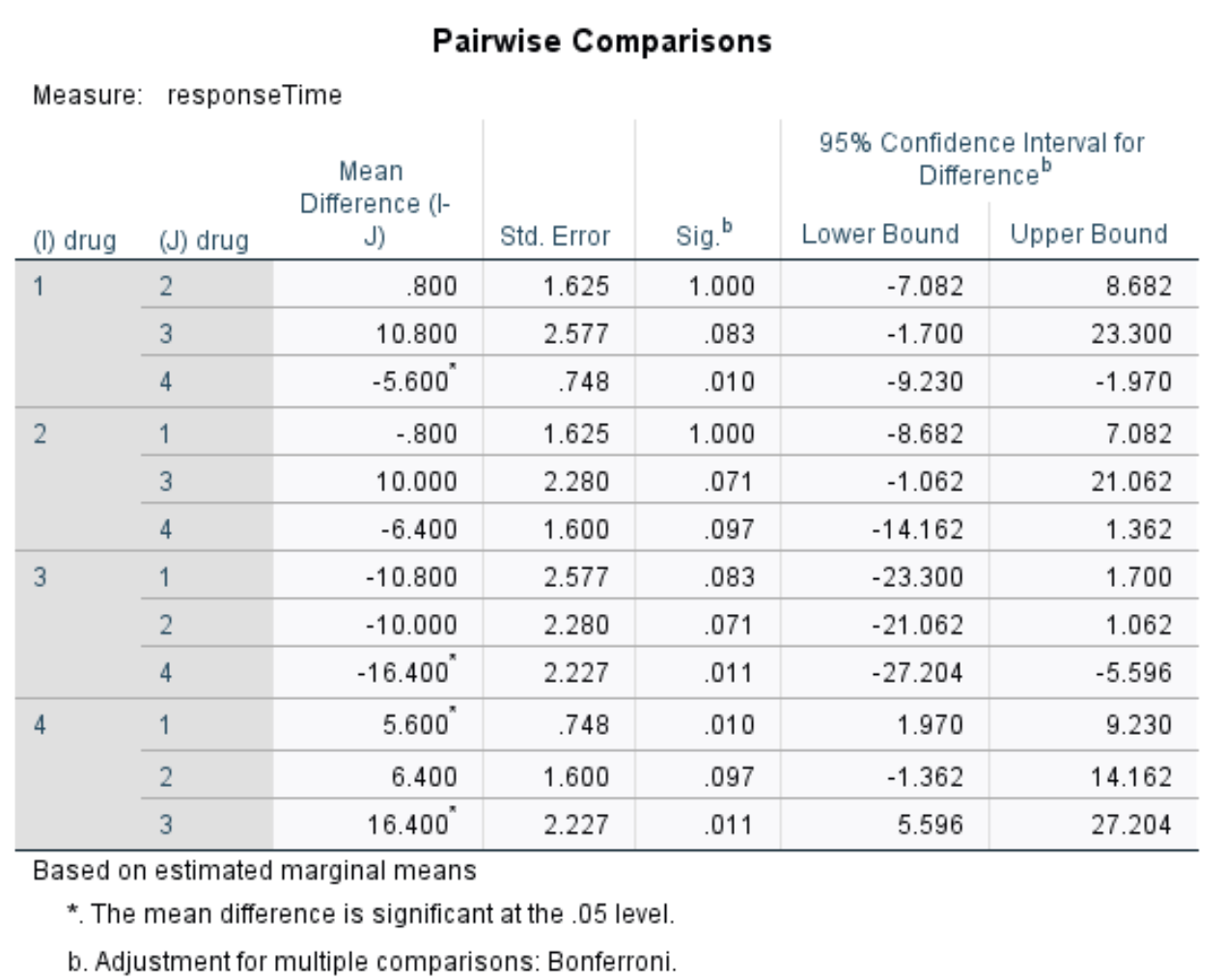
ในตารางเราจะเห็นค่า p สำหรับการเปรียบเทียบต่อไปนี้:

• ยา 1 กับ ยา 2 | ค่า p = 1.000
• ยา 1 กับ ยา 3 | ค่า p = 0.083
• ยา 1 กับ ยา 4 | ค่า p = 0.010
• ยา 2 กับ ยา 3 | ค่า p = 0.071
• ยา 2 กับ ยา 4 | ค่า p = 0.097
• ยา 3 กับ ยา 4 | ค่า p = 0.011

ค่า p เดียวที่น้อยกว่า 0.05 คือสำหรับยา 1 กับยา 4 และยา 3 กับยา 4 การเปรียบเทียบอื่นๆ ทั้งหมดมีค่า p มากกว่า 0.05

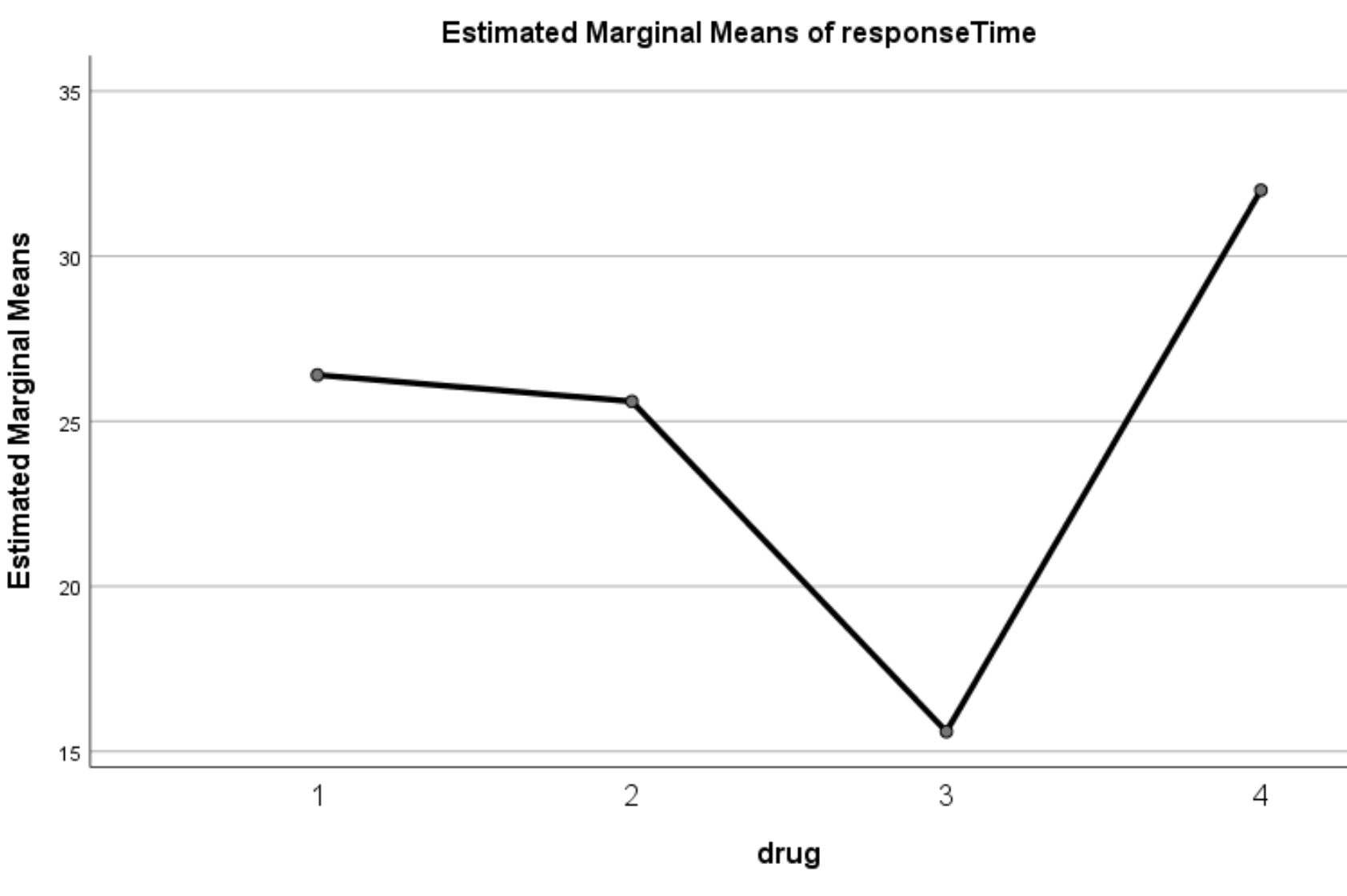
กราฟของค่าเฉลี่ยส่วนเพิ่มโดยประมาณ

แผนภูมินี้แสดงเวลาตอบสนองโดยเฉลี่ยโดยประมาณสำหรับยาแต่ละชนิด จากกราฟ เราจะเห็นได้อย่างชัดเจนว่าเวลาตอบสนองแตกต่างกันอย่างมีนัยสำคัญระหว่างยาสี่ชนิดที่แตกต่างกัน:

ขั้นตอนที่ 3: รายงานผลลัพธ์

สุดท้ายนี้เราสามารถรายงานผลลัพธ์ของการวัดความแปรปรวนแบบทำซ้ำได้ นี่คือตัวอย่างของวิธีการทำเช่นนี้:

มีการดำเนินการวิเคราะห์ความแปรปรวนแบบวัดผลทางเดียวเพื่อตรวจสอบว่าเวลาตอบสนองเฉลี่ยของผู้ป่วยแตกต่างกันระหว่างยาสี่ชนิดที่แตกต่างกันหรือไม่

การวัดความแปรปรวนแบบวัดทางเดียวซ้ำๆ เผยให้เห็นว่าประเภทของยาที่ใช้ส่งผลให้เวลาตอบสนองแตกต่างกันอย่างมีนัยสำคัญทางสถิติ (F = 24.75887, p = 0.001)

การทดสอบ Bonferroni สำหรับการเปรียบเทียบหลายรายการพบว่ามีเวลาตอบสนองที่แตกต่างกันอย่างมีนัยสำคัญทางสถิติระหว่างผู้ป่วยที่รับประทานยาที่ 1 และยาที่ 4 เช่นเดียวกับยาที่ 3 และยาที่ 4