การโอเวอร์ฟิตในแมชชีนเลิร์นนิงคืออะไร (คำอธิบายและตัวอย่าง)

ในแมชชีนเลิร์นนิง เรามักจะสร้างแบบจำลองเพื่อให้สามารถคาดการณ์ปรากฏการณ์บางอย่างได้อย่างแม่นยำ

ตัวอย่างเช่น สมมติว่าเราต้องการสร้าง แบบจำลองการถดถอย ที่ใช้ตัวแปรตัวทำนาย ชั่วโมงที่ใช้ในการศึกษา เพื่อทำนาย คะแนน ACT ของตัวแปรตอบสนองสำหรับนักเรียนมัธยมปลาย

ในการสร้างแบบจำลองนี้ เราจะรวบรวมข้อมูลเกี่ยวกับชั่วโมงที่ใช้ในการศึกษาและคะแนน ACT ที่สอดคล้องกันสำหรับนักเรียนหลายร้อยคนในเขตการศึกษาบางแห่ง

จากนั้นเราจะใช้ข้อมูลนี้เพื่อ ฝึก โมเดลที่สามารถคาดการณ์คะแนนที่นักเรียนจะได้รับตามจำนวนชั่วโมงเรียนทั้งหมด

เพื่อประเมินประโยชน์ของแบบจำลอง เราสามารถวัดได้ว่าการคาดการณ์ของแบบจำลองตรงกับข้อมูลที่สังเกตได้ดีเพียงใด หนึ่งในหน่วยเมตริกที่ใช้กันมากที่สุดในการดำเนินการนี้คือค่าคลาดเคลื่อนกำลังสองเฉลี่ย (MSE) ซึ่งคำนวณได้ดังนี้

MSE = (1/n)*Σ(y _i – f(x _i )) ²

ทอง:

• n: จำนวนการสังเกตทั้งหมด
• y _i : ค่าตอบสนองของการสังเกต ^{ครั้งที่ 3}
• f(x _i ): ค่าตอบสนองที่คาดการณ์ไว้ของการสังเกต ^{ครั้ง} ที่ i

ยิ่งการคาดการณ์แบบจำลองใกล้กับการสังเกตมากเท่าไร MSE ก็จะยิ่งต่ำลงเท่านั้น

อย่างไรก็ตาม หนึ่งในข้อผิดพลาดที่ใหญ่ที่สุดที่เกิดขึ้นในแมชชีนเลิร์นนิงคือการเพิ่มประสิทธิภาพโมเดลเพื่อลด การฝึกอบรม MSE กล่าวคือ การคาดการณ์แบบจำลองตรงกับข้อมูลที่เราใช้ฝึกโมเดลได้ดีเพียงใด

เมื่อแบบจำลองมุ่งเน้นไปที่การลด MSE การฝึกอบรมมากเกินไป ก็มักจะทำงานหนักเกินไปในการค้นหารูปแบบในข้อมูลการฝึกอบรมที่มีสาเหตุมาจากความบังเอิญ จากนั้น เมื่อนำแบบจำลองไปใช้กับข้อมูลที่มองไม่เห็น ประสิทธิภาพก็ต่ำ

ปรากฏการณ์นี้เรียกว่า การสวมใส่มากเกินไป สิ่งนี้เกิดขึ้นเมื่อเรา “พอดี” โมเดลใกล้กับข้อมูลการฝึกมากเกินไป และจบลงด้วยการสร้างแบบจำลองที่ไม่มีประโยชน์สำหรับการคาดการณ์ข้อมูลใหม่

ตัวอย่างของการโอเวอร์ฟิต

เพื่อให้เข้าใจถึงความเหมาะสมมากเกินไป เราจะกลับมาที่ตัวอย่างการสร้างแบบจำลองการถดถอยที่ใช้ เวลาหลายชั่วโมงในการศึกษา เพื่อทำนาย คะแนน ACT

สมมติว่าเรารวบรวมข้อมูลสำหรับนักเรียน 100 คนในเขตการศึกษาแห่งหนึ่ง และสร้างแผนผังกระจายอย่างรวดเร็วเพื่อแสดงภาพความสัมพันธ์ระหว่างตัวแปรทั้งสอง:

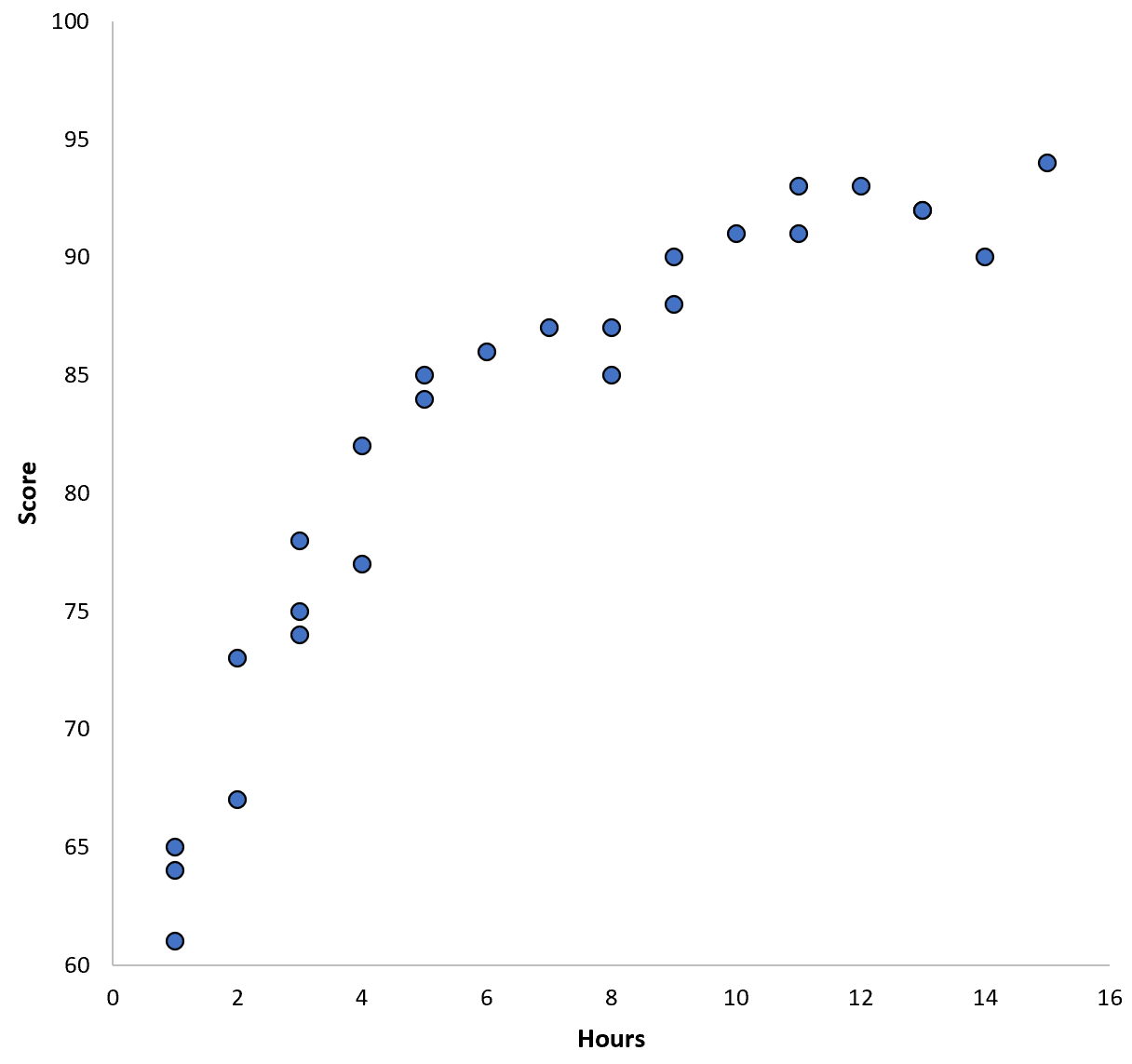
ความสัมพันธ์ระหว่างตัวแปรทั้งสองดูเหมือนจะเป็นแบบกำลังสอง ดังนั้น สมมติว่าเราใช้แบบจำลองการถดถอยกำลังสองต่อไปนี้:

คะแนน = 60.1 + 5.4*(ชั่วโมง) – 0.2*(ชั่วโมง) ²

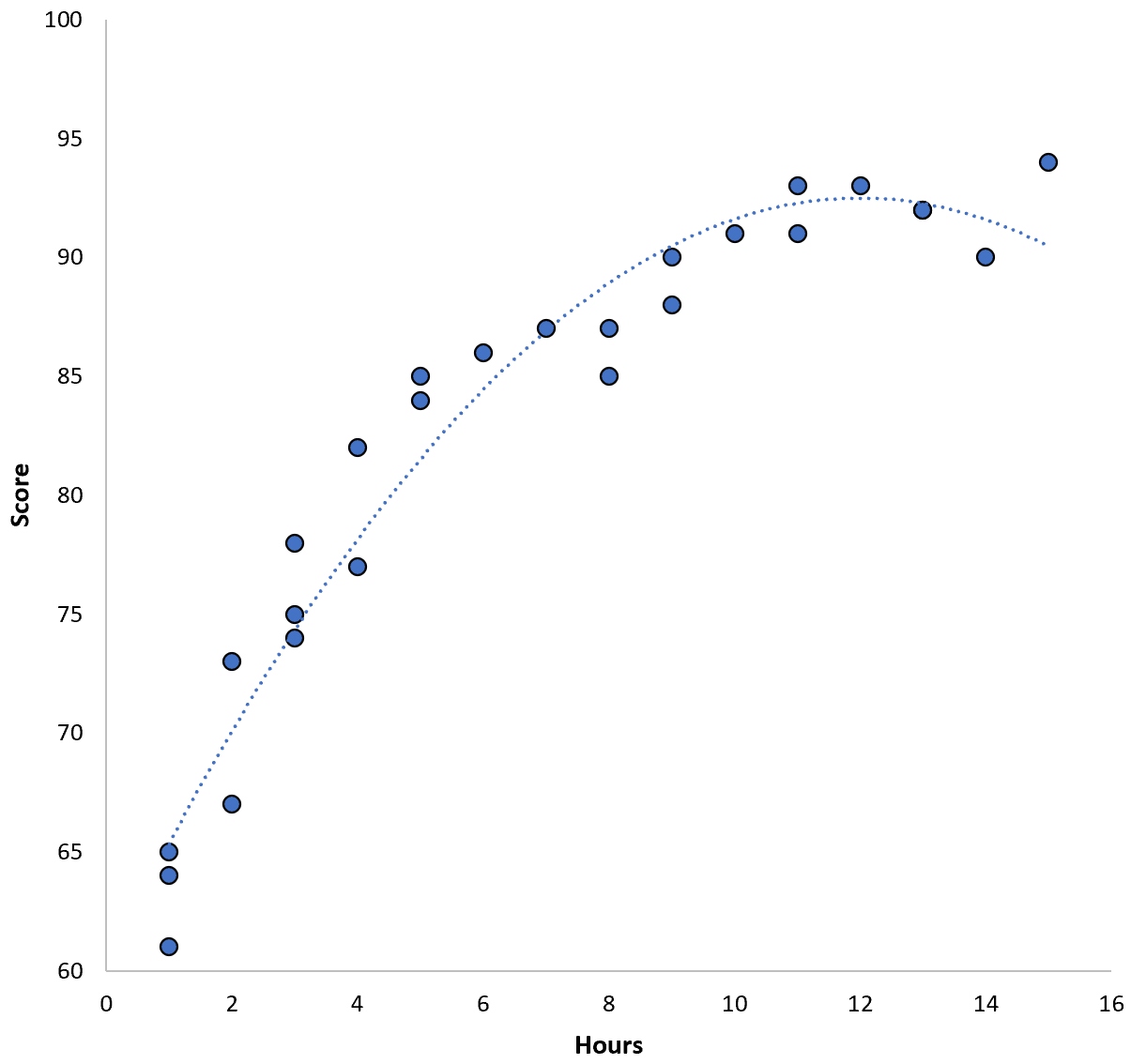
โมเดลนี้มีค่าเฉลี่ยความคลาดเคลื่อนกำลังสองเฉลี่ยในการฝึก (MSE) เท่ากับ 3.45 นั่นคือ ผลต่างกำลังสองเฉลี่ยรากระหว่างการคาดการณ์ที่ทำโดยแบบจำลองและคะแนน ACT จริงคือ 3.45

อย่างไรก็ตาม เราสามารถลดการฝึกอบรม MSE นี้ได้โดยปรับโมเดลพหุนามลำดับที่สูงกว่าให้เหมาะสม ตัวอย่างเช่น สมมติว่าเราใช้โมเดลต่อไปนี้:

คะแนน = 64.3 – 7.1*(ชั่วโมง) + 8.1*(ชั่วโมง) ² – 2.1*(ชั่วโมง) ³ + 0.2*(ชั่วโมง ^{) 4 – 0.1*(ชั่วโมง) 5 +} 0.2(ชั่วโมง) ⁶

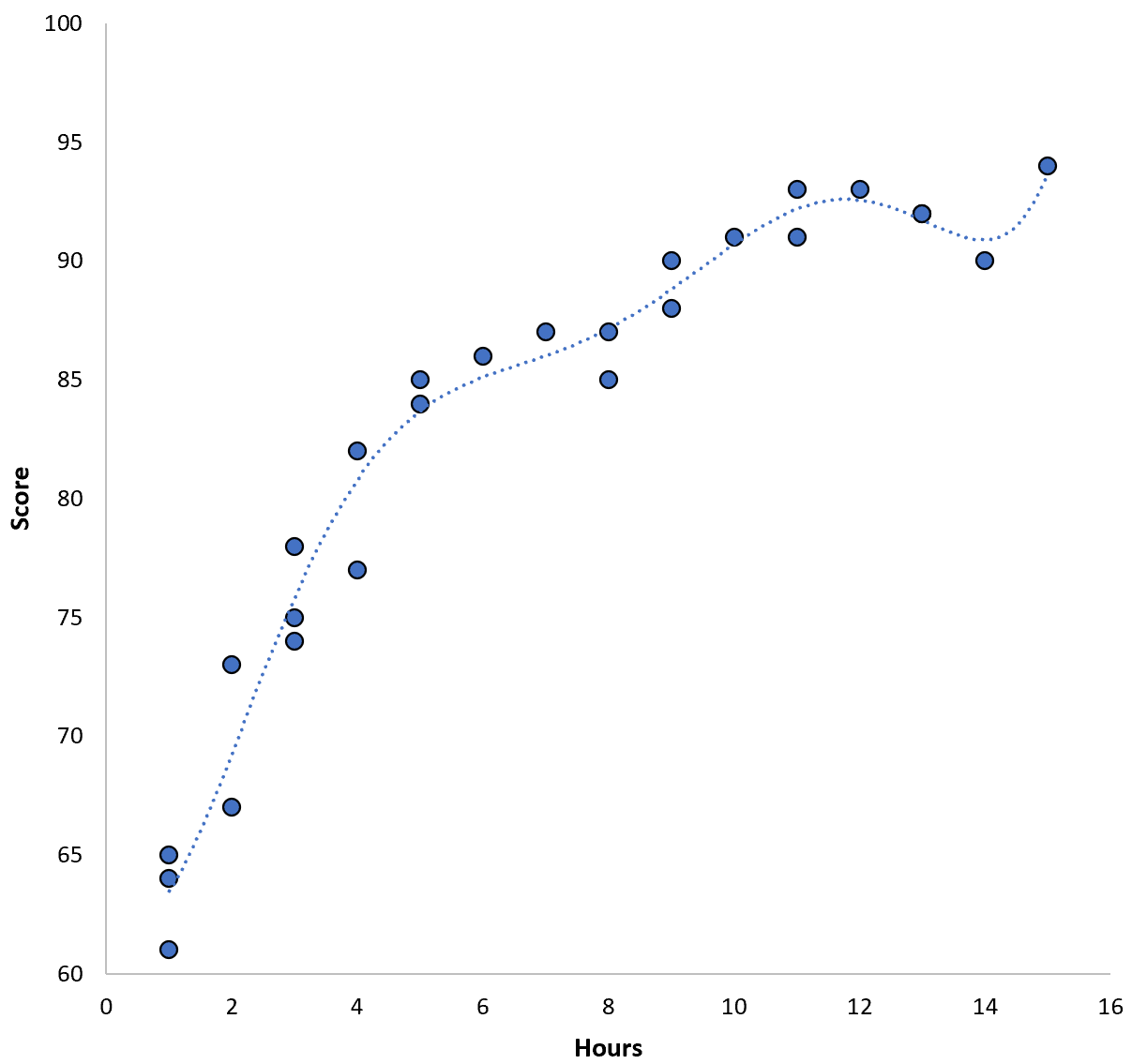
สังเกตว่าเส้นการถดถอยเหมาะสมกับข้อมูลจริงอย่างใกล้ชิดมากกว่าเส้นการถดถอยก่อนหน้ามากอย่างไร

โมเดลนี้มีข้อผิดพลาดกำลังสองเฉลี่ยรูทการฝึกอบรม (MSE) เพียง 0.89 นั่นคือ ผลต่างกำลังสองเฉลี่ยรากระหว่างการคาดการณ์ที่ทำโดยแบบจำลองและคะแนน ACT จริงคือ 0.89

การฝึกอบรม MSE นี้มีขนาดเล็กกว่าการฝึกอบรมรุ่นก่อนมาก

อย่างไรก็ตาม เราไม่สนใจเกี่ยวกับ การฝึกอบรม MSE มากนัก กล่าวคือ การคาดการณ์ของแบบจำลองตรงกับข้อมูลที่เราใช้ฝึกแบบจำลองได้ดีเพียงใด แต่เราให้ความสำคัญกับ การทดสอบ MSE เป็นหลัก ซึ่งก็คือ MSE เมื่อนำแบบจำลองของเราไปใช้กับข้อมูลที่มองไม่เห็น

หากเราใช้แบบจำลองการถดถอยพหุนามลำดับที่สูงกว่าด้านบนกับชุดข้อมูลที่มองไม่เห็น ก็มีแนวโน้มว่าจะทำงานได้แย่กว่าแบบจำลองการถดถอยกำลังสองที่ง่ายกว่า นั่นคือจะทำให้เกิดการทดสอบ MSE ที่สูงขึ้น ซึ่งเป็นสิ่งที่เราไม่ต้องการอย่างแน่นอน

วิธีการตรวจจับและหลีกเลี่ยงการสวมอุปกรณ์มากเกินไป

วิธีที่ง่ายที่สุดในการตรวจจับการติดตั้งมากเกินไปคือการตรวจสอบความถูกต้องข้าม วิธีการที่ใช้กันมากที่สุดเรียกว่า การตรวจสอบข้าม k-fold และทำงานดังนี้:

ขั้นตอนที่ 1: สุ่มแบ่งชุดข้อมูลออกเป็นกลุ่ม k หรือ “พับ” โดยมีขนาดเท่ากันโดยประมาณ

ขั้นตอนที่ 2: เลือกพับใดพับหนึ่งเป็นชุดการถือของคุณ ปรับเทมเพลตเป็นพับ k-1 ที่เหลือ คำนวณการทดสอบ MSE จากการสังเกตในชั้นที่ถูกดึง

ขั้นตอนที่ 3: ทำซ้ำขั้นตอนนี้ k ครั้ง ในแต่ละครั้งโดยใช้ชุดอื่นเป็นชุดการยกเว้น

ขั้นตอนที่ 4: คำนวณ MSE โดยรวมของการทดสอบเป็นค่าเฉลี่ยของ k MSE ของการทดสอบ

ทดสอบ MSE = (1/k)*ΣMSE _i

ทอง:

• k: จำนวนพับ
• MSE _i : ทดสอบ MSE ในการวนซ้ำครั้ง ^{ที่ 3}

การทดสอบ MSE นี้ทำให้เรามีความคิดที่ดีว่าแบบจำลองที่กำหนดจะทำงานอย่างไรกับข้อมูลที่ไม่รู้จัก

ในทางปฏิบัติ เราสามารถติดตั้งโมเดลที่แตกต่างกันได้หลายแบบ และดำเนินการตรวจสอบข้าม k-fold ในแต่ละรุ่นเพื่อค้นหาการทดสอบ MSE จากนั้นเราจึงสามารถเลือกแบบจำลองที่มีการทดสอบ MSE ต่ำสุดเป็นแบบจำลองที่ดีที่สุดเพื่อใช้ในการคาดการณ์ในอนาคต

สิ่งนี้ทำให้แน่ใจได้ว่าเราจะเลือกแบบจำลองที่น่าจะทำงานได้ดีที่สุดกับข้อมูลในอนาคต ตรงข้ามกับแบบจำลองที่ลด MSE การฝึกอบรมให้เหลือน้อยที่สุดและ “เหมาะสม” กับข้อมูลในอดีตได้ดี

แหล่งข้อมูลเพิ่มเติม

อะไรคือข้อแลกเปลี่ยนระหว่างความแปรปรวนและความแปรปรวนในแมชชีนเลิร์นนิง?
ข้อมูลเบื้องต้นเกี่ยวกับการตรวจสอบข้าม K-Fold
โมเดลการถดถอยและการจำแนกประเภทในแมชชีนเลิร์นนิง