การกระจายพหุนาม
บทความนี้จะอธิบายว่าการแจกแจงแบบพหุนามในสถิติคืออะไร ดังนั้น คุณจะพบคำจำกัดความของการแจกแจงแบบพหุนาม สูตรของมันคืออะไร แบบฝึกหัดที่แก้ไขแล้ว และคุณสมบัติของการแจกแจงความน่าจะเป็นประเภทนี้คืออะไร นอกจากนี้ คุณจะสามารถคำนวณความน่าจะเป็นของการแจกแจงพหุนามด้วยเครื่องคิดเลขออนไลน์ได้
การแจกแจงพหุนามคืออะไร?
การแจกแจงแบบพหุนาม (หรือ การแจกแจงแบบพหุนาม ) เป็นการแจกแจงความน่าจะเป็นที่อธิบายความน่าจะเป็นของเหตุการณ์ที่ไม่เกิดร่วมกันหลายเหตุการณ์ที่เกิดขึ้นตามจำนวนครั้งที่กำหนดหลังการทดลองหลายครั้ง
นั่นคือ ถ้าการทดลองสุ่มสามารถส่งผลให้เกิดเหตุการณ์พิเศษสามเหตุการณ์ขึ้นไป และทราบความน่าจะเป็นของแต่ละเหตุการณ์ที่เกิดขึ้นแยกกัน การแจกแจงแบบพหุนามจะใช้ในการคำนวณความน่าจะเป็นที่เมื่อมีการทดลองหลายครั้ง จะมีเหตุการณ์จำนวนหนึ่งเกิดขึ้น เวลาทุกครั้ง
การแจกแจงแบบพหุนามจึงเป็นลักษณะทั่วไปของการแจกแจงแบบทวินาม
สูตรการกระจายพหุนาม
ในการคำนวณ ความน่าจะเป็นของการแจกแจงพหุนาม คุณต้องหาผลหารระหว่างแฟกทอเรียลของจำนวนข้อมูลทั้งหมดกับแฟกทอเรียลของจำนวนครั้งที่เกิดขึ้นของแต่ละเหตุการณ์ จากนั้นผลลัพธ์จะคูณด้วยผลคูณของความน่าจะเป็นของแต่ละเหตุการณ์ นำมาซึ่งจำนวนเหตุการณ์ดังกล่าว
กล่าวอีกนัยหนึ่ง สูตรสำหรับการแจกแจงพหุนาม มีดังนี้

ทอง:
-
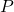
คือความน่าจะเป็นของการแจกแจงพหุนามที่คำนวณได้
-

คือจำนวนการทดสอบทั้งหมดที่ดำเนินการ
-

คือจำนวนครั้งที่เหตุการณ์เกิดขึ้น

.
-

คือความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้น

.
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณความน่าจะเป็นของตัวแปรที่ตามหลังการแจกแจงพหุนาม
ตัวอย่างการแจกแจงพหุนาม
เพื่อทำความเข้าใจแนวคิดของการแจกแจงแบบพหุนามให้เสร็จสิ้น เราได้แก้ตัวอย่างการคำนวณความน่าจะเป็นของการแจกแจงแบบพหุนามด้านล่างนี้แล้ว
- ร้านค้าขายสินค้าที่แตกต่างกันสามรายการ เมื่อลูกค้าทำการซื้อ ความน่าจะเป็นที่จะเป็นผลิตภัณฑ์ A, ผลิตภัณฑ์ B หรือผลิตภัณฑ์ C คือ 30%, 15% และ 55% ตามลำดับ ค้นหาความน่าจะเป็นที่เมื่อร้านค้าขายได้ 8 หน่วย 2 รายการเป็นผลิตภัณฑ์ A 1 รายการ B และผลิตภัณฑ์ C 5 รายการ
ปัญหาที่กำหนดอยู่ภายใต้การแจกแจงแบบพหุนาม ดังนั้นจึงจำเป็นต้องใช้สูตรสำหรับการแจกแจงความน่าจะเป็นประเภทนี้:
![]()
ดังนั้นเราจึงแทนที่ข้อมูลจากปัญหาลงในสูตรและทำการคำนวณความน่าจะเป็น:
![]()
ดังนั้นความน่าจะเป็นที่คำแถลงปัญหาบอกว่าจะเกิดขึ้นคือ 11.4%
เครื่องคำนวณการกระจายพหุนาม
เขียนจำนวนครั้งของแต่ละเหตุการณ์ในช่องแรก และความน่าจะเป็นที่จะเกิดขึ้นของแต่ละเหตุการณ์ในช่องที่สองตามลำดับเดียวกัน จากนั้นป้อนจำนวนความพยายามทั้งหมดที่ทำในช่องว่างสุดท้าย
ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม
คุณสมบัติของการแจกแจงพหุนาม
การแจกแจงพหุนามมีลักษณะดังต่อไปนี้:
- ในการแจกแจงแบบพหุนาม ค่าที่คาดหวังของจำนวนครั้งที่เหตุการณ์ i เกิดขึ้นเมื่อทำการทดลอง n ครั้งจะเท่ากับจำนวนการทดลองทั้งหมดที่ดำเนินการคูณด้วยความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้น
![]()
- ในการแจกแจงแบบพหุนาม ความแปรปรวนสำหรับเหตุการณ์ i คำนวณโดยใช้นิพจน์ต่อไปนี้
![]()
- ในทำนองเดียวกัน ความแปรปรวนร่วมระหว่างสองเหตุการณ์จะเท่ากับผลคูณของจำนวนการทดลองทั้งหมดคูณด้วยความน่าจะเป็นของแต่ละเหตุการณ์คูณด้วย -1:
![]()
- ฟังก์ชันการสร้างโมเมนต์สำหรับการแจกแจงพหุนามคือ: