ขนาดตัวอย่าง
บทความนี้จะอธิบายว่าขนาดของกลุ่มตัวอย่างคืออะไร และเหตุใดจึงมีความสำคัญในเชิงสถิติ นอกจากนี้ คุณจะได้ค้นพบวิธีการคำนวณขนาดตัวอย่างที่เหมาะสมและแบบฝึกหัดที่แก้ไขได้ เพื่อให้คุณเห็นว่ามันเสร็จสิ้นได้อย่างไร
ขนาดตัวอย่างคืออะไร?
ขนาดตัวอย่าง (หรือ ขนาดตัวอย่าง ) คือจำนวนบุคคลที่ประกอบเป็นกลุ่มตัวอย่างในการศึกษา ในเชิงสถิติ ขนาดของกลุ่มตัวอย่างมีความสำคัญเพื่อให้กลุ่มตัวอย่างเป็นตัวแทนของประชากรทั้งหมด
ดังนั้นขนาดตัวอย่างของการศึกษาทางสถิติจะต้องมีขนาดใหญ่พอที่จะแสดงถึงลักษณะของประชากรทั้งหมดได้ ในทางกลับกัน ขนาดตัวอย่างต้องไม่ใหญ่เกินไป เนื่องจากการวิจัยจะมีราคาแพงกว่า โดยสรุป ขนาดตัวอย่างควรจะเพียงพอไม่ใหญ่หรือเล็กเกินไป
ตัวอย่างเช่น หากเราต้องการวิเคราะห์ความสูงของประเทศหนึ่งๆ เราไม่สามารถถามความสูงของประชากรในประเทศทั้งหมดได้ เนื่องจากการสำรวจจะใช้เวลานานและจะมีราคาแพงเกินไป จึงจำเป็นต้องสุ่มตัวอย่างและสัมภาษณ์เฉพาะกลุ่มตัวอย่างที่เป็นตัวแทนของประชากรเท่านั้น
และเราจะทราบขนาดตัวอย่างที่เหมาะสมได้อย่างไร? ในส่วนถัดไป เราจะดูวิธีการกำหนดขนาดตัวอย่างที่เหมาะสมโดยอิงตามข้อกำหนดในการวิจัย
วิธีการคำนวณขนาดตัวอย่าง
สำหรับการประมาณค่าเฉลี่ย ขนาดตัวอย่างที่ต้องการจะเท่ากับกำลังสองของ Z α/2 คูณด้วยค่าเบี่ยงเบนมาตรฐาน (σ) หารด้วยระยะเผื่อความคลาดเคลื่อนที่ต้องการ (e) สูตรคำนวณขนาดตัวอย่าง จึงเป็นดังนี้:
![]()
ทอง:
-

คือขนาดตัวอย่าง
-
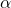
คือระดับความสำคัญที่ต้องการ โดยคำนึงถึงเรื่องนี้
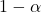
คือระดับความมั่นใจที่ต้องการ
-

คือควอไทล์ของการแจกแจงแบบปกติมาตรฐานที่สอดคล้องกับความน่าจะเป็นของ α/2 สำหรับกลุ่มตัวอย่างขนาดใหญ่และระดับความเชื่อมั่น 95% มักจะใกล้กับ 1.96 และสำหรับระดับความเชื่อมั่น 99% มักจะใกล้กับ 2.576
-

คือค่าเบี่ยงเบนมาตรฐาน
โปรดทราบว่าในสูตรนี้จะถือว่าขนาดประชากรไม่มีที่สิ้นสุด กล่าวคือ ขนาดประชากรมีขนาดใหญ่มากหรือไม่ทราบ
หมายเหตุ: สูตรข้างต้นได้มาจาก ช่วงสูตรความเชื่อมั่นสำหรับค่าเฉลี่ย
ตัวอย่างการคำนวณขนาดตัวอย่าง
ในส่วนนี้ เราจะคำนวณขนาดตัวอย่างที่เหมาะสมสำหรับการสำรวจเชิงสถิติเป็นตัวอย่าง
- เรารู้ว่าค่าเบี่ยงเบนมาตรฐานของประชากรอยู่ที่ประมาณ 15 แต่เราไม่ทราบค่าเฉลี่ย ดังนั้นเราจึงต้องการศึกษาเพื่อประมาณค่าเฉลี่ย เราต้องใช้ขนาดตัวอย่างเท่าใดหากเราต้องการค่าเผื่อความคลาดเคลื่อน ±2 โดยมีระดับความเชื่อมั่น 95%
ดังที่เราเห็นข้างต้น สูตรคำนวณขนาดตัวอย่างคือ:
![]()
ในกรณีนี้ ระดับความเชื่อมั่นที่ต้องการคือ 95% ดังนั้นค่า Z α/2 ที่สอดคล้องกันคือ 1.96
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
ในที่สุด เมื่อเรารู้ว่าพารามิเตอร์ทั้งหมดมีมูลค่าเท่าใด เราก็จะแทนค่าลงในสูตรและคำนวณขนาดตัวอย่าง:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dd8e2d30042f759051fb52c5c55ade44_l3.png)
กล่าวโดยย่อ เพื่อประมาณค่าเฉลี่ยของประชากรตามข้อกำหนดที่ต้องการ เราต้องการตัวอย่างอย่างน้อย 217 คน
ขนาดตัวอย่าง ระดับความเชื่อมั่น และส่วนต่างของข้อผิดพลาด
ขนาดตัวอย่างที่ต้องการจะแตกต่างกันไป ขึ้นอยู่กับระดับความเชื่อมั่นและขอบเขตของข้อผิดพลาดที่ต้องการ ดังนั้นขนาดตัวอย่าง ระดับความเชื่อมั่น และส่วนต่างของข้อผิดพลาดจึงสัมพันธ์กันดังนี้:
- ขนาดตัวอย่างและระดับความเชื่อมั่นเป็นสัดส่วนโดยตรง นั่นคือหากระดับความเชื่อมั่นเพิ่มขึ้น ขนาดของกลุ่มตัวอย่างก็จะเพิ่มขึ้นด้วย
- ขนาดตัวอย่างและระยะขอบของข้อผิดพลาดเป็นสัดส่วนผกผัน ดังนั้นหากระยะขอบของข้อผิดพลาดเพิ่มขึ้น ขนาดตัวอย่างก็จะลดลง
- ดังนั้นการเพิ่มขนาดตัวอย่างจะช่วยเพิ่มระดับความเชื่อมั่นหรือลดส่วนต่างของข้อผิดพลาดได้
สูตรขนาดตัวอย่างอื่นๆ
สูตรสำหรับขนาดตัวอย่างที่จำเป็นจะแตกต่างกันไปเล็กน้อย ขึ้นอยู่กับพารามิเตอร์ที่จะประมาณ ดังนั้นในส่วนนี้เราจะมาดูสูตรอื่นๆ ที่เป็นประโยชน์ในการคำนวณขนาดตัวอย่างในบางกรณีพิเศษ
ขนาดตัวอย่างตามสัดส่วน
สูตรคำนวณขนาดตัวอย่างที่จำเป็นในการประมาณสัดส่วน (p) คือ:
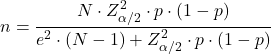
ขนาดตัวอย่างของความน่าจะเป็น
เมื่อคุณต้องการประมาณความน่าจะเป็น ขอแนะนำให้ใช้สูตรต่อไปนี้เพื่อกำหนดขนาดตัวอย่างที่จำเป็น:
![]()
ขนาดตัวอย่างสำหรับการเปรียบเทียบสองวิธีอิสระ
สูตรการคำนวณขนาดตัวอย่างเมื่อเปรียบเทียบสองวิธีอิสระกับความเสี่ยง α และความเสี่ยง β ที่กำหนดมีดังนี้:
![]()
ทอง
![]()
คือความแตกต่างระหว่างสองวิธีของสมมติฐานทางเลือก
ขนาดตัวอย่างสำหรับการเปรียบเทียบวิธีจับคู่สองวิธี
หากคุณต้องการเปรียบเทียบค่าเฉลี่ยสองค่าที่จับคู่กันกับข้อผิดพลาดคงที่ α และข้อผิดพลาด β สูตรที่ใช้ค้นหาจำนวนการสังเกตในกลุ่มตัวอย่างคือ:
![]()
ทอง
![]()
คือความแตกต่างระหว่างสองค่าเฉลี่ยที่จับคู่กันของสมมติฐานทางเลือกและ
![]()
มันคือความแปรปรวนของความแตกต่างระหว่างการวัดสองครั้งของคนคนเดียวกัน