คำแนะนำเกี่ยวกับขั้นตอนของ benjamini-hochberg

ทุกครั้งที่คุณทำการทดสอบทางสถิติ เป็นไปได้ว่าคุณจะได้ค่า p น้อยกว่า 0.05 ตามความบังเอิญ แม้ว่าสมมติฐานว่างของคุณจะเป็นจริงก็ตาม

ตัวอย่างเช่น สมมติว่าคุณต้องการทราบว่าต้นไม้บางชนิดมีความสูงเฉลี่ยมากกว่า 10 นิ้วหรือไม่ สมมติฐานว่างและทางเลือกของคุณสำหรับการทดสอบคือ:

สูง ₀ : μ = 10 นิ้ว

H _A : μ > 10 นิ้ว

เพื่อทดสอบสมมติฐานนี้ คุณสามารถออกไป สุ่มตัวอย่าง พืช 20 ต้นเพื่อวัด แม้ว่าความสูงเฉลี่ยที่แท้จริงของพืชชนิดนี้คือ 10 นิ้ว แต่ก็เป็นไปได้ว่าคุณได้เลือกตัวอย่างพืชที่สูงผิดปกติจำนวน 20 ต้น ซึ่งนำคุณไปสู่การปฏิเสธสมมติฐานที่เป็นโมฆะ

แม้ว่าสมมติฐานว่างจะเป็นจริง (ความสูงเฉลี่ยของต้นนี้คือ 10 นิ้ว) คุณก็ปฏิเสธ ในทางสถิติ เราเรียกสิ่งนี้ว่า “การค้นพบที่ผิดพลาด” คุณอ้างว่าได้ทำการค้นพบ – “ผลลัพธ์ที่สำคัญ” – แต่จริงๆ แล้วนี่เป็นเท็จ

ทีนี้ลองจินตนาการว่าทำการทดสอบทางสถิติ 100 ครั้งพร้อมกัน เมื่อใช้ ระดับอัลฟ่า 0.05 มีโอกาสเพียง 5% ที่จะค้นพบเท็จด้วยการทดสอบแต่ละรายการ แต่เนื่องจากคุณกำลังทำการทดสอบจำนวนมาก คุณจึงคาดหวังได้ว่าจะมีเพียง 5 ใน 100 เท่านั้นที่นำไปสู่การค้นพบที่ผิดพลาด

ในโลกสมัยใหม่ การค้นพบที่ผิดพลาดอาจเป็นปัญหาที่พบบ่อยได้เนื่องจากเทคโนโลยีช่วยให้นักวิจัยทำการทดสอบทางสถิติได้ครั้งละหลายร้อยหรือหลายพันครั้ง

ตัวอย่างเช่น นักวิจัยทางการแพทย์สามารถทำการทดสอบทางสถิติกับยีนได้หลายหมื่นยีนในแต่ละครั้ง แม้ว่าจะมีอัตราการค้นพบที่ผิดพลาดเพียง 5% นั่นหมายความว่าการทดสอบหลายร้อยครั้งอาจส่งผลให้เกิดการค้นพบที่ผิดพลาดได้

วิธีหนึ่งในการควบคุมอัตราการค้นพบที่ผิดพลาดคือการใช้สิ่งที่เรียกว่า ขั้นตอน Benjamini-Hochberg

ขั้นตอนเบนจามินิ-ฮอชเบิร์ก

ขั้นตอน Benjamini-Hochberg ทำงานดังนี้:

ขั้นตอนที่ 1: ทำการทดสอบทางสถิติทั้งหมดของคุณและค้นหาค่า p สำหรับการทดสอบแต่ละครั้ง

ขั้นตอนที่ 2: จัดอันดับค่า p ตามลำดับจากมากไปน้อย กำหนดอันดับให้กับแต่ละรายการ: ค่าที่น้อยที่สุดมีอันดับ 1 ค่าที่น้อยที่สุดถัดไปมีอันดับ 2 เป็นต้น

ขั้นตอนที่ 3: คำนวณค่า Benjamini-Hochberg ที่สำคัญสำหรับค่า p แต่ละค่า โดยใช้สูตร (i/m)*Q

ทอง:

i = อันดับของค่า p

m = จำนวนการทดสอบทั้งหมด

Q = อัตราการค้นพบเท็จที่คุณเลือก

ขั้นตอนที่ 4: ค้นหาค่า p ที่ใหญ่ที่สุดที่น้อยกว่าค่าวิกฤต กำหนดให้แต่ละค่า p น้อยกว่าค่า p นี้ว่ามีนัยสำคัญ

ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการขั้นตอนนี้ด้วยค่าที่เป็นรูปธรรม

ตัวอย่าง

สมมติว่านักวิจัยต้องการตรวจสอบว่าตัวแปร 20 ตัวที่เกี่ยวข้องกับโรคหัวใจหรือไม่ พวกเขาทำการทดสอบทางสถิติครั้งละ 20 ครั้ง และรับค่า p สำหรับการทดสอบแต่ละครั้ง ตารางต่อไปนี้แสดงค่า p สำหรับการทดสอบแต่ละรายการโดยเรียงจากมากไปน้อย

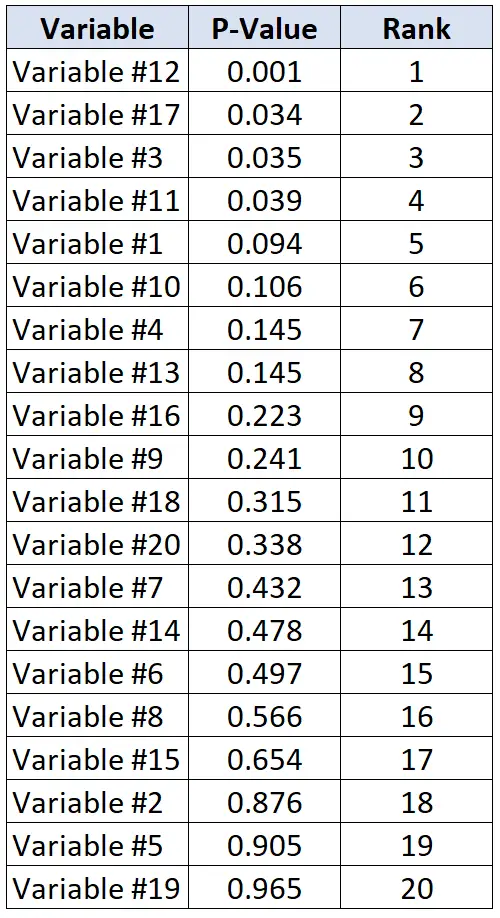
สมมติว่านักวิจัยยินดียอมรับอัตราการค้นพบที่ผิดพลาดที่ 20% ดังนั้น ในการคำนวณค่าเบนจามินิ-ฮอชเบิร์กที่สำคัญสำหรับค่า p แต่ละค่า เราสามารถใช้สูตรต่อไปนี้: (i/20)*0.2 โดยที่ i = อันดับของค่า p

ตารางต่อไปนี้แสดงค่า Benjamini-Hochberg ที่สำคัญสำหรับค่า p แต่ละค่า:

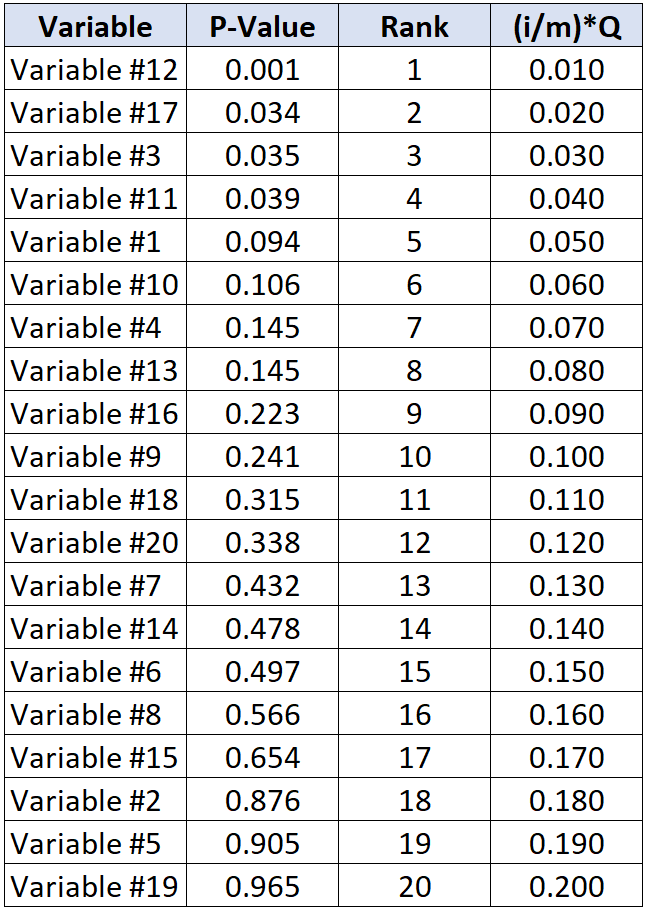
การทดสอบที่มีค่า p มากที่สุดต่ำกว่าค่าวิกฤต Benjamini-Hochberg คือตัวแปร #11 ซึ่งมีค่า p เท่ากับ 0.039 และค่าวิกฤต BH เท่ากับ 0.040

ดังนั้นการทดสอบนี้และการทดสอบทั้งหมดที่มีค่า p น้อยกว่าจะถือว่ามีนัยสำคัญ

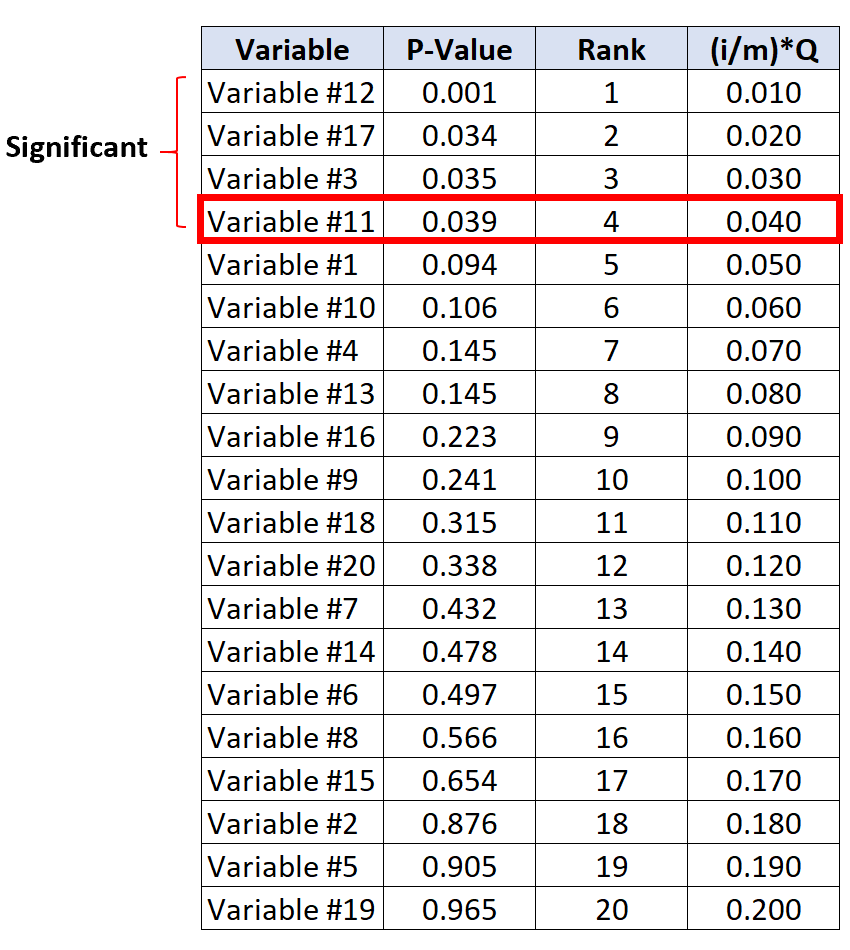
โปรดทราบว่าแม้ว่าตัวแปร #17 และ #3 จะไม่มีค่า p น้อยกว่าค่าวิกฤต BH แต่ก็ยังถือว่ามีนัยสำคัญเนื่องจากมีค่า p น้อยกว่าตัวแปร #11

วิธีเลือกอัตราการค้นพบที่ผิดพลาด

ขั้นตอนที่สำคัญที่สุดประการหนึ่งในขั้นตอนของ Benjamini-Hochberg คือการเลือกอัตราการค้นพบที่ผิดพลาด คุณควรเลือกอัตราการค้นพบที่ผิดพลาดก่อนที่จะรวบรวมข้อมูลหรือทำการทดสอบทางสถิติ

โดยทั่วไป คุณจะทำการทดสอบทางสถิติจำนวนมากในระหว่างขั้นตอนการสำรวจการวิเคราะห์ของคุณ ซึ่งจากนั้นคุณจะติดตามผลการทดสอบอื่นๆ เพื่อสำรวจผลลัพธ์ของคุณเพิ่มเติม

หากการทดสอบติดตามผลมีราคาไม่แพง คุณอาจพิจารณากำหนดอัตราการค้นพบที่ผิดพลาดให้สูงขึ้น เนื่องจากแม้ว่าคุณจะมีการค้นพบที่ผิดพลาดบ้าง คุณก็มีแนวโน้มที่จะค้นพบการค้นพบที่ผิดพลาดเหล่านั้นในการทดสอบครั้งต่อไป

นอกจากนี้ หากการพลาดการค้นพบที่สำคัญมีค่าใช้จ่ายสูง คุณอาจต้องการเพิ่มอัตราการค้นพบที่ผิดพลาดเพื่อที่คุณจะได้ไม่พลาดสิ่งสำคัญ

ขึ้นอยู่กับค่าใช้จ่ายในการวิจัยของคุณและความสำคัญของการไม่พลาดการค้นพบที่สำคัญใดๆ อัตราการค้นพบที่ผิดพลาดจะแตกต่างกันไปในแต่ละสถานการณ์

แหล่งข้อมูลเพิ่มเติม

คำอธิบายค่า P และนัยสำคัญทางสถิติ
อัตราข้อผิดพลาดต่อตระกูลคือเท่าใด