ความสัมพันธ์เชิงบวก
ในบทความนี้ คุณจะได้เรียนรู้ว่าความสัมพันธ์เชิงบวกหมายถึงอะไรในสถิติ ตัวอย่างของตัวแปรที่มีความสัมพันธ์เชิงบวก และความแตกต่างระหว่างความสัมพันธ์ประเภทอื่นๆ
ความสัมพันธ์เชิงบวกคืออะไร?
ในสถิติ ความสัมพันธ์เชิงบวก คือความสัมพันธ์ประเภทหนึ่งระหว่างตัวแปรสองตัวที่แตกต่างกัน โดยเฉพาะอย่างยิ่ง ความสัมพันธ์เชิงบวกระหว่างตัวแปรสองตัวหมายความว่า หากค่าของตัวแปรตัวหนึ่งเพิ่มขึ้น ตัวแปรอีกตัวหนึ่งก็จะเพิ่มขึ้นเช่นกัน
เพื่อให้พิจารณา ความสัมพันธ์ระหว่างตัวแปรทั้งสอง เป็นค่าบวก ค่าของสัมประสิทธิ์สหสัมพันธ์ต้องอยู่ระหว่าง 0 (ไม่รวม) ถึง 1 (รวม)
โปรดทราบว่าความสัมพันธ์เชิงบวกสามารถเรียก ว่าความสัมพันธ์โดยตรง ได้
ตัวอย่างความสัมพันธ์เชิงบวก
เมื่อพิจารณาคำจำกัดความของความสัมพันธ์เชิงบวก ด้านล่างคือตัวอย่างของตัวแปรสองตัวที่แสดงความสัมพันธ์ดังกล่าว
- ในตารางความถี่ต่อไปนี้ จะรวบรวมคะแนนคณิตศาสตร์และสถิติของกลุ่มตัวอย่างนักเรียน 20 คนเป็นข้อมูล วิเคราะห์ความสัมพันธ์ระหว่างตัวแปรทั้งสอง
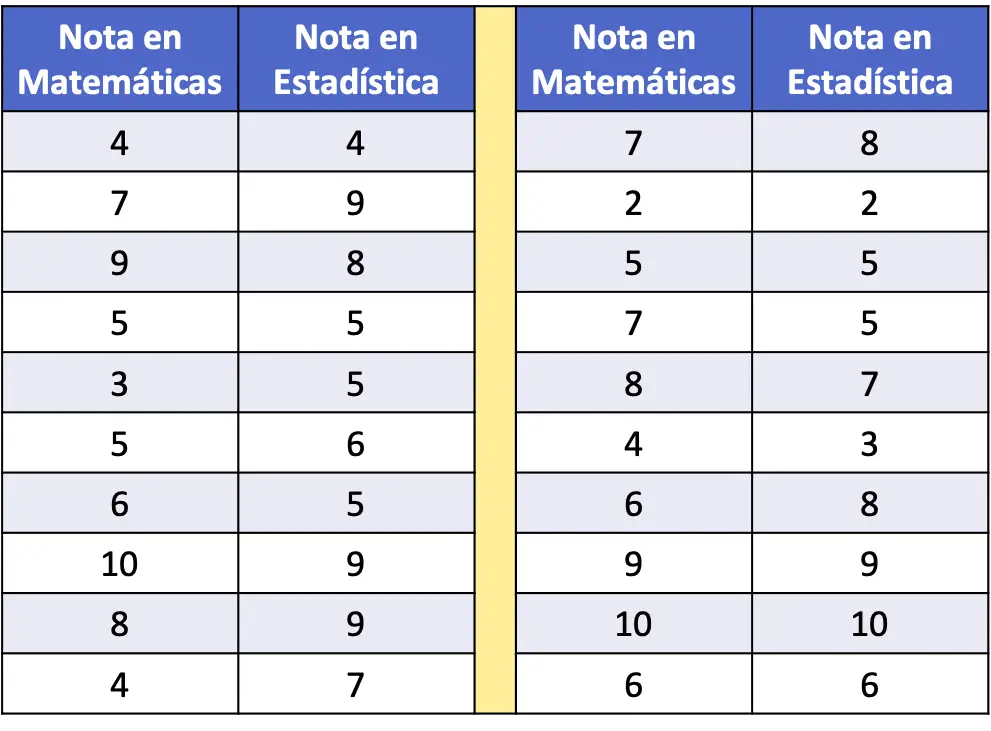
ก่อนที่จะคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ ขอแนะนำให้แสดงข้อมูลทางสถิติที่ตั้งไว้ในแผนภาพกระจายก่อนเพื่อการสำรวจเบื้องต้น
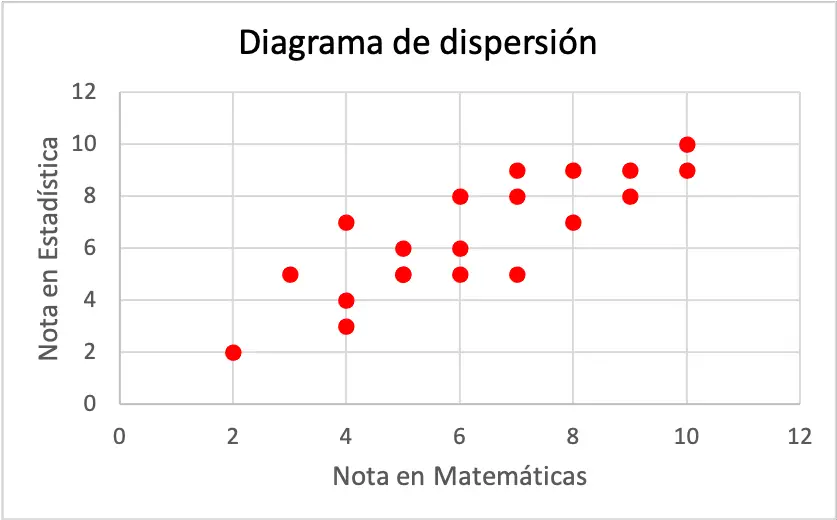
ดังที่กราฟแสดง ปรากฏว่าตัวแปรทั้งสองมีความสัมพันธ์เชิงเส้นเชิงบวก เนื่องจากเมื่อเกรดคณิตศาสตร์เพิ่มขึ้น เกรดสถิติก็จะเพิ่มขึ้นด้วย แต่เพื่อกำหนดประเภทของความสัมพันธ์อย่างแน่ชัดจำเป็นต้อง คำนวณค่าสัมประสิทธิ์สหสัมพันธ์ :
![]()
ค่าของสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันมากกว่า 0 และใกล้เคียงกับ 1 มาก ดังนั้นความสัมพันธ์ระหว่างตัวแปรทั้งสองที่ศึกษาจึงเป็นค่าบวกอย่างแน่นอน
การตีความความสัมพันธ์เชิงบวก
เพื่อทำความเข้าใจความหมายของความสัมพันธ์เชิงบวกในสถิติ เราจะมาดูวิธีตีความค่าความสัมพันธ์เชิงบวกระหว่างตัวแปรสองตัวในส่วนนี้
ยิ่งค่าสัมประสิทธิ์สหสัมพันธ์มีค่าสูง ตัวแปรทั้งสองก็จะมีความสัมพันธ์เชิงบวกมากขึ้นเท่านั้น ดังนั้น เมื่อค่าสัมประสิทธิ์สหสัมพันธ์เข้าใกล้ 1 แสดงว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นเป็นค่าบวกและแข็งแกร่งมาก
ในทางกลับกัน เมื่อค่าสัมประสิทธิ์สหสัมพันธ์ต่ำและใกล้ศูนย์ หมายความว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองเป็นบวกแต่อ่อนแอ แม้ว่าค่าสัมประสิทธิ์สหสัมพันธ์จะกลายเป็นศูนย์หรือลบ ก็หมายความว่าความสัมพันธ์นั้นเป็นศูนย์หรือลบตามลำดับ ด้านล่างนี้เราจะเห็นความแตกต่างระหว่างความสัมพันธ์ทั้งสามประเภทนี้
ท้ายที่สุด ควรสังเกตว่าความสัมพันธ์เชิงบวกไม่ได้หมายความถึงสาเหตุระหว่างตัวแปร นั่นคือ หากตัวแปรสองตัวมีความสัมพันธ์กันในเชิงบวก นั่นหมายความว่าตัวแปรทั้งสองมีความสัมพันธ์กันเชิงเส้น แต่ตัวแปรตัวหนึ่งไม่จำเป็นต้องเป็นสาเหตุของอีกตัวแปรหนึ่งเสมอไป
เช่นเดียวกับส่วนก่อนหน้า คะแนนในวิชาคณิตศาสตร์และสถิติมีความสัมพันธ์เชิงบวก แต่การได้เกรดที่ดีในวิชาคณิตศาสตร์ไม่ได้รับประกันว่าจะได้เกรดที่ดีในวิชาสถิติโดยอัตโนมัติ แต่จะต้องเรียนทั้งสองวิชา สรุปแล้ว เกรดในวิชาคณิตศาสตร์ไม่ใช่สาเหตุของเกรดในวิชาสถิติ ตัวแปร 2 ตัวเชื่อมโยงกันง่ายๆ
ความสัมพันธ์เชิงบวก ลบ และศูนย์
นอกจากความสัมพันธ์เชิงบวกแล้ว ในสถิติแล้ว ตัวแปรสองตัวยังสามารถมีความสัมพันธ์เชิงลบหรือเป็นศูนย์ได้อีกด้วย ดังนั้นในส่วนนี้เราจะมาดูกันว่าความสัมพันธ์ทั้งสามประเภทนี้แตกต่างกันอย่างไร
- ความสัมพันธ์เชิงบวก : ตัวแปรหนึ่งจะเพิ่มขึ้นเมื่ออีกตัวแปรหนึ่งเพิ่มขึ้นเช่นกัน ค่าของสัมประสิทธิ์สหสัมพันธ์อยู่ระหว่าง 0 (ไม่รวม) ถึง 1 (รวม)
- ความสัมพันธ์เชิงลบ : เมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งก็จะลดลง และในทางกลับกัน หากตัวแปรตัวหนึ่งลดลง อีกตัวแปรหนึ่งก็จะเพิ่มขึ้น ค่าของสัมประสิทธิ์สหสัมพันธ์อยู่ระหว่าง -1 (รวม) ถึง 0 (ไม่รวม)
- Zero correlation : ไม่มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง ค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0
ในแผนภูมิต่อไปนี้ คุณสามารถดูความสัมพันธ์แต่ละประเภทที่แสดง:
