เหตุใดโหมดจึงมีความสำคัญในสถิติ
โหมด นี้แสดงถึงค่าที่ปรากฏบ่อยที่สุดในชุดข้อมูล
ชุดข้อมูลไม่สามารถมีโหมดได้ (หากไม่มีค่าซ้ำ) โหมดเดียวหรือหลายโหมด
ตัวอย่างเช่น โหมดในชุดข้อมูลต่อไปนี้คือ 19:
ชุดข้อมูล: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26
นี่คือค่าที่ปรากฏบ่อยที่สุด
ในสถิติ โหมดมีความสำคัญด้วยเหตุผลต่อไปนี้:
เหตุผลที่ 1 : สิ่งนี้ช่วยให้เราทราบว่าค่าใดในชุดข้อมูลที่พบบ่อยที่สุด
เหตุผลที่ 2 : มีประโยชน์ในการค้นหาค่าที่พบบ่อยที่สุดในข้อมูลเชิงหมวดหมู่ เมื่อไม่สามารถคำนวณค่าเฉลี่ยและค่ามัธยฐานได้
เหตุผลที่ 3 : ช่วยให้เข้าใจได้ว่า “ศูนย์กลาง” ของชุดข้อมูลอยู่ที่ใด แม้ว่าค่ามัธยฐานและค่าเฉลี่ยจะใช้กันทั่วไปมากกว่า (ดังที่เราจะดูในบทความนี้ต่อไป)
ตัวอย่างต่อไปนี้แสดงให้เห็นถึงเหตุผลแต่ละข้อเหล่านี้ในทางปฏิบัติ
เหตุผลที่ 1: โหมดบอกเราว่าค่าใดที่พบบ่อยที่สุด
สมมติว่าเรามีชุดข้อมูล 100,000 แถวซึ่งประกอบด้วยราคาขายบ้านในสหรัฐอเมริกา:

สมมติว่าเราใช้ซอฟต์แวร์ทางสถิติ (เช่น Excel , R , Python ฯลฯ ) เพื่อคำนวณโหมดของชุดข้อมูลนี้และพบว่ามีสามโหมด:
- 280,000 ดอลลาร์
- 300,000 ดอลลาร์
- 305,000 ดอลลาร์
สิ่งนี้ช่วยให้เราทราบราคาบ้านที่พบบ่อยที่สุดในชุดข้อมูลได้ทันที
การคำนวณโหมดหลักพันยังเร็วกว่าการดูแถวข้อมูลและพยายามระบุว่าราคาบ้านใดเกิดขึ้นบ่อยที่สุด
เหตุผลที่ 2: โหมดจะค้นหาค่าที่พบบ่อยที่สุดในข้อมูลหมวดหมู่
สมมติว่าเรามีชุดข้อมูล 1,000 แถวที่บอกเราเกี่ยวกับสีของรถที่บุคคลในละแวกใกล้เคียงเป็นเจ้าของ:
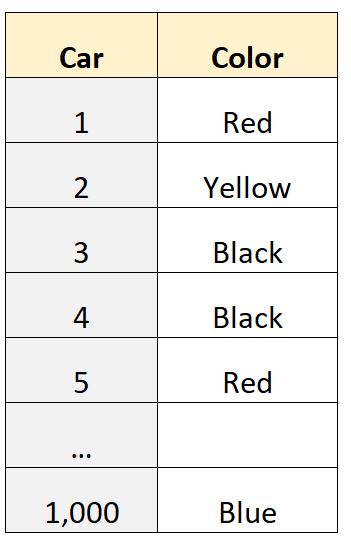
ตัวแปร “สี” เป็น ตัวแปรเชิงหมวดหมู่ ซึ่งหมายความว่าค่าอยู่ในหมวดหมู่ (“สีแดง”, “สีเหลือง”, “สีดำ” ฯลฯ ) ดังนั้นเราจึงไม่สามารถคำนวณค่าเชิงปริมาณเช่นค่าเฉลี่ยหรือค่ามัธยฐาน .
อย่างไรก็ตาม เราสามารถคำนวณโหมดได้เนื่องจากโหมดนี้เป็นเพียงการแสดงค่าที่พบบ่อยที่สุดในชุดข้อมูล
ตัวอย่างเช่น เราสามารถใช้ซอฟต์แวร์ทางสถิติเพื่อพิจารณาว่าโหมดของชุดข้อมูลนี้คือ “สีดำ” ซึ่งบอกเราว่าสีรถที่พบบ่อยที่สุดในชุดข้อมูลนี้คือสีดำ
เหตุผลที่ 3: โหมดช่วยให้เราทราบว่าศูนย์กลางของชุดข้อมูลอยู่ที่ไหน
โหมดนี้ยังถือเป็นการ วัดแนวโน้มจากศูนย์กลาง ซึ่งหมายความว่าจะทำให้เราทราบว่า “ศูนย์กลาง” ของชุดข้อมูลอยู่ที่ไหน
ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงคะแนนสอบของนักเรียนที่แตกต่างกัน 20 คนในชั้นเรียน:

โหมดนี้กลายเป็น 82 ซึ่งเป็นคะแนนสอบที่พบบ่อยที่สุด นอกจากนี้ยังเป็นข้อบ่งชี้ที่ดีว่าค่าคะแนนรีวิว “หลัก” อยู่ที่ใดในชุดข้อมูลนี้
อย่างไรก็ตาม สมมติว่าเรามีชุดข้อมูลผลการสอบดังต่อไปนี้แทน:
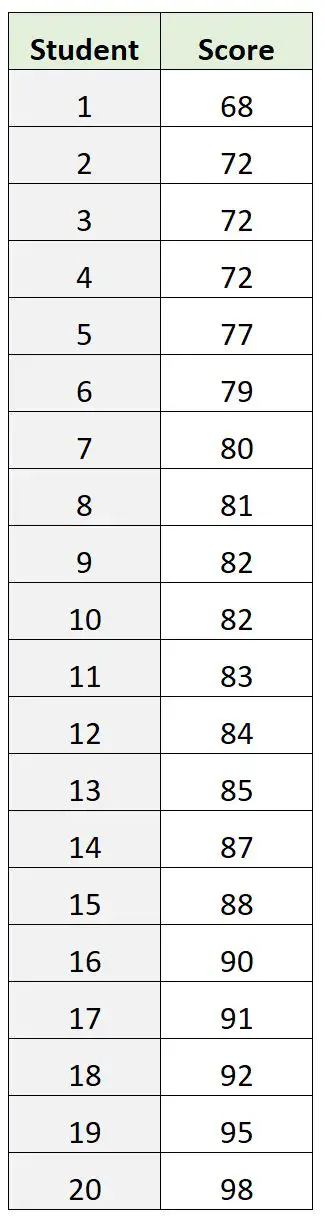
ในชุดข้อมูลนี้ 72 คือคะแนนสอบแฟชั่น อย่างไรก็ตาม สิ่งนี้กลายเป็นข้อบ่งชี้ที่ไม่ดีว่าคะแนน “หลัก” ของการสอบอยู่ตรงไหน
คะแนนสอบเฉลี่ยอยู่ที่ 82.9 และคะแนนสอบเฉลี่ยอยู่ที่ 82.5 ซึ่งทั้งสองอย่างนี้ช่วยให้เราเข้าใจได้ดีขึ้นว่าค่า “ส่วนกลาง” สัมพันธ์กับแฟชั่นตรงไหน
สรุป
นี่เป็นบทสรุปโดยย่อของประเด็นหลักที่กล่าวถึงในบทความนี้:
- โหมดนี้แสดงถึงค่าที่ปรากฏบ่อยที่สุดในชุดข้อมูล
- โหมดนี้จะบอกเราถึงค่าที่พบบ่อยที่สุดในข้อมูลหมวดหมู่ เมื่อไม่สามารถใช้ค่าเฉลี่ยและค่ามัธยฐานได้
- โหมดนี้ช่วยให้เราทราบว่า “ศูนย์กลาง” ของชุดข้อมูลอยู่ที่ใด แต่อาจทำให้เข้าใจผิดได้เมื่อเปรียบเทียบกับค่าเฉลี่ยหรือค่ามัธยฐาน
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับค่าเฉลี่ย ค่ามัธยฐาน และโหมดในสถิติ:
เหตุใดค่าเฉลี่ยจึงมีความสำคัญในสถิติ?
เหตุใดค่ามัธยฐานจึงมีความสำคัญในสถิติ?
ตัวอย่างที่เป็นรูปธรรม: การใช้ค่าเฉลี่ย ค่ามัธยฐาน และโหมด
เมื่อใดควรใช้ Mean vs. ค่ามัธยฐาน: พร้อมตัวอย่าง