คะแนน stanine คืออะไร? (คำจำกัดความและตัวอย่าง)
คะแนน Stanine ย่อมาจาก “คะแนนมาตรฐานเก้า” เป็นวิธีหนึ่งในการวัดคะแนนการทดสอบในระดับเก้าจุดมาตรฐาน
เมื่อใช้วิธีนี้ เราสามารถแปลงผลการทดสอบแต่ละรายการจากคะแนนเดิม (เช่น 0 ถึง 100) เป็นตัวเลขระหว่าง 1 ถึง 9
เราใช้กระบวนการสองขั้นตอนง่ายๆ ในการปรับผลการทดสอบให้เข้ากับคะแนน Stanine:
1. จัดอันดับผลการทดสอบแต่ละรายการจากต่ำสุดไปสูงสุด
2. ให้คะแนน 4% ต่ำสุดให้คะแนน Stanine 1 คะแนน คะแนนต่ำสุด 7% ถัดไปให้ 2 คะแนน และอื่นๆ ตามตารางต่อไปนี้:

โดยทั่วไปเราจะพิจารณาผลการทดสอบดังนี้
- Stanines 1, 2, 3: ต่ำกว่าค่าเฉลี่ย
- สตานิน 4, 5, 6: เฉลี่ย
- Stanines 7, 8, 9: สูงกว่าค่าเฉลี่ย
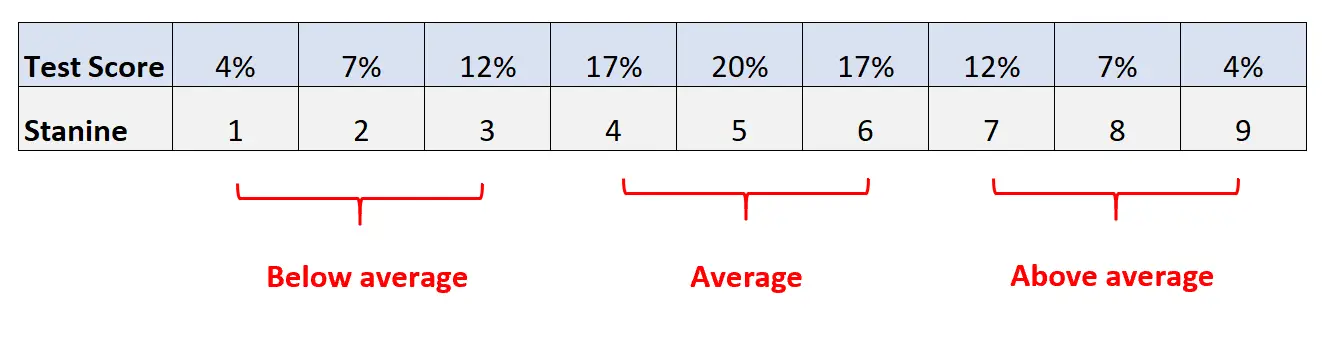
ปรากฎว่ามาตราส่วน Stanine มีค่าเฉลี่ยเป็น 5 และส่วนเบี่ยงเบนมาตรฐานเป็น 2
ข้อดีและข้อเสียของคะแนน Stanine
คะแนน Stanine มีข้อดีและข้อเสียดังต่อไปนี้:
ข้อดี: คะแนน Stanine ช่วยให้เราเข้าใจได้อย่างรวดเร็วว่าคะแนนการทดสอบที่กำหนดนั้นสัมพันธ์กับผลการทดสอบอื่นๆ ทั้งหมดอย่างไร
ตัวอย่างเช่น เรารู้ว่านักเรียนที่มีคะแนนสอบ Stanine 5 จะอยู่ในช่วงกลาง 20% ของคะแนนสอบทั้งหมด และเรารู้ว่านักเรียนคนหนึ่งที่ตกอยู่ในสตานีน 9 มีคะแนนสอบอยู่ใน 4% แรกของคะแนนทั้งหมด
ข้อเสีย: ข้อเสียของการใช้สตานีนคือ สตานีนแต่ละตัวมีขนาดไม่เท่ากัน และคะแนนการทดสอบในสตานีนที่กำหนดอาจใกล้เคียงกับคะแนนของสตานีนตัวถัดไปมากกว่าเมื่อเทียบกับคะแนนของสตานีนในตัวมันเอง
ตัวอย่างเช่น นักเรียนที่ทำคะแนนระหว่างเปอร์เซ็นไทล์ที่ 40 ถึง 60 ทั้งหมดจะถูกจัดกลุ่มอยู่ในระดับ 5 อย่างไรก็ตาม นักเรียนที่มีคะแนนสอบอยู่ในเปอร์เซ็นไทล์ที่ 58 จะต้องใกล้เคียงกับคะแนนที่ได้รับในระดับ 6 มากกว่าคะแนนส่วนใหญ่ ได้รับในสตานีน 5
ทางเลือกคะแนน Stanine
ทางเลือกสองทางนอกเหนือจากคะแนนสตานีนคือคะแนนเปอร์เซ็นไทล์และคะแนน z
1. เปอร์เซ็นไทล์ บอกเราถึงเปอร์เซ็นต์ของคะแนนทั้งหมดที่คะแนนการทดสอบที่กำหนดตกไป
ตัวอย่างเช่น คะแนนที่เปอร์เซ็นไทล์ที่ 90 สูงกว่า 90% ของคะแนนการทดสอบทั้งหมด คะแนนสอบที่เปอร์เซ็นไทล์ที่ 50 จะอยู่ตรงกลางของคะแนนสอบทั้งหมดพอดี
2. คะแนน z บอกเราว่าคะแนนที่กำหนดมีค่าเบี่ยงเบนมาตรฐานจากค่าเฉลี่ยเป็นจำนวนเท่าใด มีการคำนวณดังนี้:
z = (X – μ) / σ
ทอง:
- X คือค่าข้อมูลดิบค่าเดียว
- μ คือค่าเฉลี่ยของชุดข้อมูล
- σ คือค่าเบี่ยงเบนมาตรฐานของชุดข้อมูล
เราตีความคะแนน z ดังนี้:
- คะแนน z ที่เป็นบวกบ่งชี้ว่าคะแนนการทดสอบ สูงกว่า ค่าเฉลี่ย
- คะแนน z ติดลบแสดงว่าคะแนนการทดสอบ ต่ำกว่า ค่าเฉลี่ย
- คะแนน z ที่เป็นศูนย์บ่งชี้ว่าคะแนนการทดสอบ เท่ากับ ค่าเฉลี่ยทุกประการ
ยิ่งคะแนน z มาจากศูนย์มากเท่าไร คะแนนการทดสอบที่กำหนดก็จะยิ่งห่างจากค่าเฉลี่ยมากขึ้นเท่านั้น
คะแนน Z และเปอร์เซ็นไทล์ช่วยให้เราเข้าใจได้อย่างแม่นยำยิ่งขึ้นว่าคะแนนการทดสอบมีอันดับอย่างไรเมื่อเปรียบเทียบกับคะแนน Stanine